Слайд 2
Функция n переменных
Переменная u называется функцией n переменных
(аргументов) x,y,z,…,t, если каждой системе значений x,y,z,…,t, из области
их изменений (области определения), соответствует определенное значение u.
Областью определения функции называется совокупность всех точек, в которых она имеет определенные действительные значения.
Для функции двух переменных z=f(x,y) область определения представляет некоторую совокупность точек плоскости, а для функции трех переменных u=f(x,y,z) –некоторую совокупность точек пространства.
Слайд 3
Функция двух переменных
Функцией двух переменных называется закон, по
которому каждой паре значений независимых переменных x,y (аргументов) из области определения соответствует
значение зависимой переменной z (функции).
Данную функцию обозначают следующим образом: z = z(x,y) либо z= f(x,y) , или же другой стандартной буквой: u=f(x,y) , u = u (x,y)
Слайд 4
Частные производные первого порядка
Частной производной от функции z
=f(x,y) по независимой переменной х называется конечный предел
вычисленный
при постоянной у
Частной производной по у называется конечный предел
вычисленный при постоянной х
Для частных производных справедливы обычные правила и формулы дифференцирования.
Слайд 5
Полный дифференциал
Полный дифференциал функции z =f(x,y) вычисляется по
формуле
Полный дифференциал функции трех аргументов u =f(x,y,z) вычисляется
по формуле
Слайд 6
Частные производные высших порядков
Частными производными второго порядка от
функции z =f(x,y) называются частные производные от ее частных
производных первого порядка
Аналогично определяются и обозначаются частные производные третьего и высших порядков
.
Слайд 7
Дифференциалы высших порядков
Дифференциалом второго порядка от функции z=f(x,y)
называется дифференциал от ее пологого
Дифференциалы высших порядков вычисляются по
формуле
Имеет место символическая формула
Слайд 8
Дифференцирование сложных функций
Пусть z=f(x,y), где х=φ(t), у=ψ(t) и
функции f(x,y), φ(t), ψ(t) дифференцируемы. Тогда производная сложной функции
z=f[φ(t),ψ(t)] вычисляется по формуле
Слайд 9
Дифференцирование неявных функций
Производные неявной функции двух переменных z=f(x,y),
заданной с помощью уравнения F(x,y,z)=0, могут быть вычислены по
формулам
Слайд 10
Экстремум функции
Функции z=f(x,y) имеет максимум (минимум) в
точке M0(x0;y0) если значение функции в этой точке больше
(меньше), чем ее значение в любой другой точке M(x;y) некоторой окрестности точки M0.
Если дифференцируемая функция z=f(x,y) достигает экстремума в точке M0(x0;y0), то ее частные производные первого порядка в этой точке равны нулю, т.е.
(необходимые условия экстремума).
Слайд 11
Пусть M0(x0;y0) - стационарная точка функции z=f(x,y). Обозначим
И
составим дискриминант Δ=AC-B2. Тогда:
Если Δ>0, то функция имеет в
точке М0 экстремум, а именно максимум при А<0 (или С<0) и минимум А>0 (или С>0);
Если Δ<0, то в точке М0 экстремума нет (достаточные условия наличия или отсутствия экстремума);
Если Δ=0, то требуется дальнейшее исследование (сомнительный случай).
Слайд 13
Первообразная функция
Функция F(x) называется первообразной для функции f(x)
на интервале X=(a,b), если в каждой точке этого интервала
f(x) является производной для F(x), т.е.
Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования: по заданной функции f(x) требуется найти функцию F(x), производная которой равна f(x).
Слайд 14
Неопределённый интеграл
Множество всех первообразных функции F(x)+С для f(x)
называется неопределённым интегралом от функции f(x) и обозначается символом
. Таким образом, по определению
где C - произвольная постоянная;
f(x) - подынтегральная функция;
f(x) dx - подынтегральное выражение;
x - переменная интегрирования;
- знак неопределенного интеграла.
Слайд 15
Свойства неопределённого интеграла
1. Дифференциал от неопределенного интеграла равен
подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:
2.
Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
Слайд 16
3. Постоянный множитель можно вынести за знак интеграла:
4.
Неопределенный интеграл от алгебраической суммы конечного числа непрерывной функций
равен алгебраической сумме интегралов от слагаемых функций:
5. Если , то и где u=φ(x)- произвольная функция, имеющая непрерывную производную
Слайд 17
Таблица неопределённых интегралов
Слайд 18
Основные методы интегрирования
Метод интегрирования, при котором данный интеграл
путем тождественных преобразований подынтегральной функции (или выражения) и применения
свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
Метод непосредственного интегрирования
Слайд 19
При сведении данного интеграла к табличному часто используются
следующие преобразования дифференциала (операция «подведения под знак дифференциала»):
Слайд 20
Замена переменной в неопределённом интеграле (интегрирование подстановкой)
Метод интегрирования
подстановкой заключается во введении новой переменной интегрирования. При этом
заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.
Пусть требуется вычислить интеграл . Сделаем подстановку х = φ(t), где φ(t) - функция, имеющая непрерывную производную.
Тогда dx=φ'(t)dt и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой
Слайд 21
Интегрирование по частям
Формула интегрирования по частям
Формула дает возможность
свести вычисление интеграла к вычислению интеграла
, который может оказаться существенно более простым, чем исходный.
Слайд 22
Интегрирование рациональных дробей
Рациональной дробью называется дробь вида P(x)/Q(x),
где P(x) и Q(x) – многочлены. Рациональная дробь называется
правильной, если степень многочлена P(x) ниже степени многочлена Q(x); в противном случае дробь называется неправильной.
Простейшими (элементарными) дробями называются правильные дроби следующего вида:
где А, В, p, q, a - действительные числа.
Слайд 23
Найдем интегралы от простейших дробей
Слайд 24
Первый интеграл простейшей дроби IV типа в правой
части равенства легко находится с помощью подстановки х2+px+q=t, а
второй преобразуем так:
Полагая х+р/2=t, dx=dt и обозначая q-p2/4=a2, получим
Слайд 25
Интегрирование рациональных дробей с помощью разложения на простейшие
дроби
Перед интегрированием рациональной дроби P(x)/Q(x) надо сделать следующие алгебраические
преобразования и вычисления:
Если дана неправильная рациональная дробь, то выделить из нее целую часть, т.е. представить в виде
где М(х)-многочлен, а P1(x)/Q(x) – правильная рациональная дробь;
2) Разложить знаменатель дроби на линейные и квадратичные множители:
где р2/4-q<0, т.е. трехчлен х2+рх+q имеет комплексные сопряженные корни;
Слайд 26
3) Правильную рациональную дробь разложить на простейшие дроби:
4)
Вычислить неопределенные коэффициенты А1, А2, …, Аm, …, В1,
В2, …, Вm, …, С1, С2, …, Сm, …, для чего привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов.
Слайд 27
Интегрирование простейших иррациональных функций
Интегралы вида
где R – рациональная
функция; m1,n1,m2,n2,…- целые числа.
С помощью подстановки ах+b=ts, где s-
наименьшее общее кратное чисел n1,n2,…, указанный интеграл преобразуется в интеграл от рациональной функции.
2. Интеграл вида
Такие интегралы путем выделения квадрата из квадратного трехчлена приводятся к табличным интегралам 15 или 16
Слайд 28
3. Интеграл вида
Для нахождения этого интеграла выделим
в числителе производную квадратного трехчлена, стоящего под знаком корня,
и разложим интеграл на сумму интегралов:
Слайд 29
4.Интегралы вида
С помощью подстановки х-α=1/t этот интеграл приводится
к рассмотренному п.2
5. Интеграл вида
где Рn(х) – многочлен
n-й степени. Интеграл такого вида находится с помощью тождества
где Qn-1(x) – многочлен (n-1)-й степени с неопределенными коэффициентами, λ- число.
Дифференцируя указанное тождество и приводя результат к общему знаменателю, получим равенство двух многочленов, из которого можно определить коэффициенты многочлена Qn-1(x) и число λ.
Слайд 30
6. Интегралы от дифференциальных биномов
где m, n,
p – рациональные числа.
Как доказал П.Л. Чебышев, интегралы от
дифференциальных биномов выражаются через элементарные функции только в трех случаях:
р – целое число, тогда данный интеграл сводится к интегралу от рационнальной функции с помощью подстановки х=ts, где s – наименьшее общее кратное знаменателей дробей m и n.
(m+1)/n – целое число, в этом случае данный интеграл рационализируется с помощью подстановки a+bxn=ts;
(m+1)/n+р – целое число, в этом случае к той же цели ведет подстановка ax-n+b=ts , где s – знаменатель дроби р.
Слайд 31
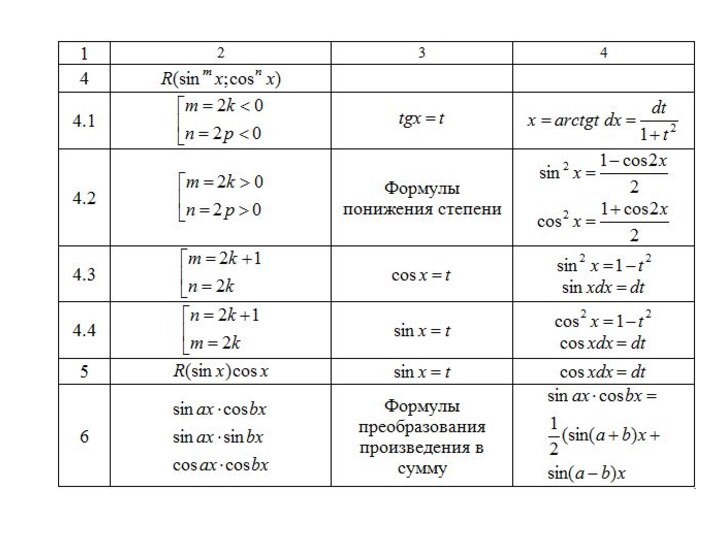
Интегрирование тригонометрических функций
Интегралы вида
где R – рациональная функция.
Под
знаком интеграла находится рациональная функция от синуса и косинуса.
В данном случае применима универсальная тригонометрическая подстановка tg(x/2)=t, которая сводит этот интеграл к интегралу от рациональной функции нового аргумента t (таблица п.1).
Существуют и другие подстановки, представленные в следующей таблице:
Слайд 35
Определенным интегралом от функции f(x) на отрезке [a;b]
называется предел интегральных сумм при условии, что длина наибольшего
частичного отрезка Δхi стремится к нуль.
Числа а и b называются нижним и верхним пределами интегрирования.
Теорема Коши. Если функция f(x) непрерывна на отрезке [a;b], то определенный интеграл существует
Слайд 36
Если f(x)>0 на отрезке [a;b], то определенный интеграл
геометрически представляет собой площадь криволинейной трапеции - фигуры, ограниченной
линиями у=f(x), x=a, x=b, y=0
Слайд 37
Свойства определенного интеграла
Слайд 39
Правила вычисления определенных интегралов
Формула Ньютона-Лейбница:
где F(x) – первообразная
для f(x), т.е. F(x)‘= f(x).
2. Интегрирование по частям:
где u=u(x),
v=v(x) – непрерывно дифференцируемые функции на отрезке [a;b].
Слайд 40
3. Замена переменной
где х=φ(t) – функция, непрерывная вместе
со своей производной φ‘ (t) на отрезке α≤t≤β, a=
φ(a), b= φ(β), f[φ(t)] – функция непрерывна на [α; β]
4. Если f(x) – нечетная функция, т.е. f(-x)=-f(x), то
Если f(x) –четная функция, т.е. f(-x)=f(x), то
.
Слайд 41
Несобственные интегралы
Несобственными интегралами называются:
1) интегралы с бесконечными
пределами;
2) интегралы от неограниченных функций.
Несобственный интеграл от функции f(x)
в пределах от а до +бесконечности определяется равенством
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если же предел не существует или равен бесконечности, - расходящимися
Если функция f(x) имеет бесконечный разрыв в точке с отрезка [a;b] и непрерывна при а≤х<с и c<х≤b, то по определению полагают
.
Слайд 42
При исследовании сходимости несобственных интегралов пользуются одним из
признаков сравнения.
1. Если функции f(x) и φ(x) определены для
всех х≥а и интегрируемы на отрезке [a;А], где А≥а, и если 0≤f(x)≤φ(x) для
всех х≥а, то из сходимости интеграла вытекает
сходимость интеграла , причем
2.1 Если при х→+∞ функция f(x)≤0 является бесконечно малой
порядка р>0 по сравнению с 1/х, то интеграл
сходится при р>1 и расходится при р≤1.
2.2 Если функция f(x)≥0 определена и непрерывна в промежутке а ≤ х1/(b-x) при х→b-0, то интеграл сходится при р<1 и
расходится при р ≥1.
.
Слайд 43
Вычисление площади плоской фигуры
Площадь криволинейной трапеции, ограниченной кривой
у=f(x) [f(x)≥0], прямыми x=a и x=b и отрезком [a;b]
оси ОХ вычисляется по формуле
Площадь фигуры, ограниченной кривой у=f1(x) и у=f2(x) [f1(x)≤f2(x)] и прямыми x=a и x=b находится по формуле
Если кривая задана параметрическими уравнениями х=х(t), у=у(t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b и отрезком [a;b] оси ОХ вычисляется по формуле
где t1 и t2 определяются из уравнения а=х(t1), b=х(t2) [y(t)≥0 при t1≤t≤t2]
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением ρ=ρ(θ) и двумя полярными радиусами θ=α, θ=β (α<β), находятся по формуле
.
Слайд 44
Вычисление длины дуги плоской кривой
Если кривая у=f(x) на
отрезке [a;b] – гладкая (т.е. производная у’=f’(x) непрерывна), то
длина соответствующей дуги этой кривой находится по формуле
При параметрическом задании кривой х=х(t), у=у(t) [х(t) и у(t) – непрерывно дифференцируемые функции] длина дуги кривой, соответствующая, монотонному изменению параметра t от t1 до t2, вычисляется по формуле
Если гладкая кривая задана в полярных координатах уравнением ρ=ρ(θ), α≤θ≤β, то длина дуги равна
.
Слайд 45
Вычисление объема тела
1. Вычисление объема тела по известным
площадям поперечных сечений. Если площадь сечения тела плоскость, перпендикулярной
оси ОХ, может быть выражена как функция от х, т.е. в виде S=S(х) (a≤x≤b), объем части тела, заключенный между перпендикулярными оси ОХ плоскостями x=a и x=b, находится по формуле
2. Вычисление объема тела вращения. Если криволинейная трапеция, ограниченная кривой у=f(x) и прямыми у=0, x=a, x=b, вращается вокруг оси ОХ, то объем тела вращения вычисляется по формуле
Если фигура, ограниченная кривыми у1=f1(x) и у2=f2(x) [0≤f1(x)≤f2(x)] и прямыми x=a, x=b, вращается вокруг оси ОХ, то объем тема вращения равен
.
Слайд 46
Вычисление площади поверхности вращения
Если дуга гладкой кривая у=f(x)
(a≤х≤b) вращается вокруг оси ОХ, то площадь поверхности вращения
вычисляется по формуле
Если кривая задана параметрическими уравнениями х=х(t), у=у(t) (t1≤t≤t2), то
.
Слайд 47
Обыкновенные дифференциальные уравнения
Слайд 48
Основные понятия
Дифференциальным уравнением называется уравнение, связывающее независимые переменные,
их функцию и производные (или дифференциалы) этой функции.
Если
независимая переменная одна, то уравнение называется обыкновенным, если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.
Слайд 49
Уравнение первого порядка
Функциональное уравнение F(x,y,y) = 0 или
y= f(x,y), связывающее между собой независимую переменную, искомую функцию
y(x) и ее производную y(x), называется дифференциальным уравнением первого порядка.
Решением уравнения первого порядка называется всякая функция y=(x), которая, будучи подставлена в уравнение вместе со своей производной y=(x), обращает его в тождество относительно x.
Слайд 50
Общее решение дифференциального уравнения 1-го порядка
Общим решением дифференциального
уравнения первого порядка называется такая функция y = (x,C),
которая при любом значении параметра C является решением этого дифференциального уравнения. Уравнение Ф(x,y,C)=0, определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
Слайд 51
Уравнение, разрешенное относительно производной
Если уравнение 1-го порядка разрешить
относительно производной, то оно может быть представлено в виде
Его общее решение геометрически представляет собой семейство интегральных кривых, т. е. совокупность линий, соответствующих различным значениям постоянной C.
Слайд 52
Постановка задачи Коши
Задача отыскания решения дифференциального уравнения
,
удовлетворяющего начальному условию
при ,называется задачей Коши для уравнения 1-го порядка.
Геометрически это означает: найти интегральную кривую дифференциального уравнения , проходящую через данную точку .
Слайд 53
Уравнение с разделяющимися переменными
Дифференциальное уравнение
называется уравнением с разделенными переменными.
Дифференциальное уравнение 1-го
порядка называется уравнением с разделяющимися переменными, если оно имеет вид:
Для решения уравнения делят обе его части на произведение функций , а затем интегрируют.
Слайд 54
Однородные уравнения
Дифференциальное уравнение первого
порядка называется однородным, если его можно привести к виду
y=
или к виду
где и – однородные функции одного порядка .
Слайд 55
Линейные уравнения 1-го порядка
Дифференциальное уравнение
первого порядка называется линейным, если оно содержит у
и у‘ в первой степени, т.е. имеет вид
.
Решают такое уравнение с помощью подстановки y=uv, где u и v-вспомогательные неизвестные функции, которые находят, подставляя в уравнение вспомогательные функции и на одну из функций налагают определенные условия.
Слайд 56
Уравнение Бернулли
Уравнением Бернулли называется уравнение 1-го
порядка, имеющее вид
,
где и
Его, как и линейное уравнение решают с помощью подстановки
Слайд 57
Дифференциальные уравнения
2-го порядка
Уравнение 2-го порядка
имеет вид
Или
Общим решением уравнения второго
порядка называется такая функция , которая при любых значениях параметров является решением этого уравнения.
Слайд 58
Задача Коши для уравнения 2-го порядка
Если
уравнение 2-го порядка разрешить относительно второй производной, то для
такого уравнения имеет место задача: найти решение уравнения ,
удовлетворяющее начальным условиям:
и
Эту задачу называют задачей Коши для дифференциального уравнения 2-гопорядка.
Слайд 59
Теорема существования и единственности решения уравнения 2-го порядка
Если в уравнении
функция
и ее частные производные по аргументам и непрерывны в некоторой области, содержащей точку , то существует и притом единственное решение этого уравнения, удовлетворяющее условиям
и .
Слайд 60
Уравнения 2-го порядка, допускающие понижение порядка
Простейшее уравнение
2-го порядка
решают двукратным интегрированием.
Уравнение , не содержащее явно у, решают с помощью подстановки
,
Уравнение , не содержащее х, решают заменой
, .
Слайд 61
Линейные однородные уравнения
Линейным однородным дифференциальным уравнением
второго порядка называется уравнение
Если все коэффициенты этого уравнения постоянны, то уравнение называется уравнением с постоянными коэффициентами .
Слайд 62
Свойства решений линейного однородного уравнения
Теорема 1.
Если у(х) является решением уравнения , то и Су(х),
где С-константа, также является решением этого уравнения.
Слайд 63
Свойства решений линейного однородного уравнения
Теорема 2. Если
и
-решения уравнения, то и их сумма также является решением этого уравнения.
Следствие. Если и -решения уравнения, то функция
-также решение этого уравнения.
Слайд 64
Линейно зависимые и линейно независимые функции
Две
функции и
называются линейно зависимыми на некотором промежутке, если можно подобрать такие числа и ,не равные нулю одновременно, что линейная комбинация этих функций тождественно равна нулю на этом промежутке, т. е.
Слайд 65
Если таких чисел подобрать нельзя, то
функции и
называются линейно независимыми на указанном промежутке.
Функции и будут линейно
зависимыми тогда и только тогда, когда их отношение постоянно, т. е.
Слайд 66
Теорема о структуре общего решения линейного однородного уравнения
2-го порядка
Если
и -линейно независимые частные решения ЛОУ 2-го порядка, то их линейная комбинация
где и -произвольные постоянные, является общим решением этого уравнения.

































![Дифференциальное исчисление функций нескольких переменных Определенным интегралом от функции f(x) на отрезке [a;b] называется предел интегральных сумм](/img/tmb/14/1339261/88984d434f74c436a969e9f71aeb196f-720x.jpg)
![Дифференциальное исчисление функций нескольких переменных Если f(x)>0 на отрезке [a;b], то определенный интеграл геометрически представляет собой площадь](/img/tmb/14/1339261/41704fa3a60d1b909d0e76a89c5f62d2-720x.jpg)






![Дифференциальное исчисление функций нескольких переменных Вычисление площади плоской фигурыПлощадь криволинейной трапеции, ограниченной кривой у=f(x) [f(x)≥0], прямыми x=a](/img/tmb/14/1339261/46e3ecc12a1c0c5040334b12694ce674-720x.jpg)
![Дифференциальное исчисление функций нескольких переменных Вычисление длины дуги плоской кривойЕсли кривая у=f(x) на отрезке [a;b] – гладкая](/img/tmb/14/1339261/991dfb190a50eea952b67d01806256f0-720x.jpg)