Слайд 2
ВВЕДЕНИЕ
Человек подобен дроби: в знаменателе - то, что он о себе думает, в числителе - то, что он есть на самом деле.

Чем больше знаменатель, тем меньше дробь.
(Л.Н. Толстой)
Необходимость в дробных числах возникла у человека
на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых
животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.
Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры. Исторически дроби возникли в процессе измерения.
Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей.
Слайд 3
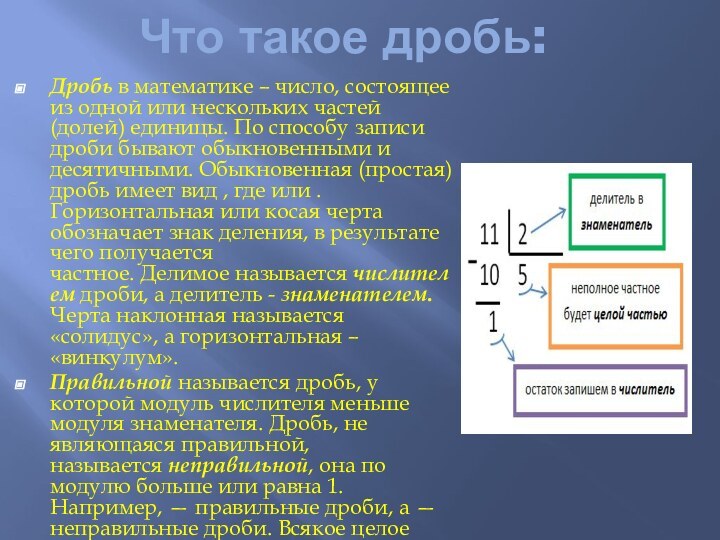
Что такое дробь:
Дробь в математике – число, состоящее из одной или нескольких частей (долей) единицы. По способу записи дроби бывают обыкновенными и десятичными. Обыкновенная (простая) дробь имеет вид , где или . Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимое называется числителем дроби, а делитель - знаменателем. Черта наклонная называется «солидус», а горизонтальная – «винкулум».
Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной, она по модулю больше или равна 1. Например, — правильные дроби, а — неправильные дроби. Всякое целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.
Слайд 4
Впервые дроби появились в Древнем Вавилоне где-то за

2000 лет до новой эры и были шестидесятеричными: их
знаменатель равнялся 60,меньшая единица измерения составляла 1/60 часть высшей единицы. Полностью эта система выдерживалась у вавилонян для измерения времени и углов, и мы унаследовали от них деление часа и градуса на 60 минут, а минуты на 60 секунд, их мера измерения называлась шестидесятеричная система.
Математикой в Вавилоне занимались жрецы, они же в своих занятиях столкнулись со случаями, когда нужно было знать соотношение чисел, друг на друга не делящихся.
Жрецы просто подобрали число, которое достаточно развитый человек еще может удержать в уме, имеющее максимальное количество простых делителей. В самом деле, 60 делится и на 2, и на 3, и на 5, и соответственно, на все кратные им числа без остатка. Знаменатель 60 вавилонских дробей был своего рода эталоном для сравнения чисел.
Но для средних умов – купцов, ремесленников, строителей – основание 60 было все же слишком большим. И плохо согласовывалось с удобным для практики счетом на пальцах рук, которых 10. Да и особых значков для цифр тогда еще не было; все действия записывались словами.
Запись дроби по Вавилонским правилам (только цифрами)1/7 примерно выглядела так 1/7 ≈ 1/60 +1/60 +1/60 +1/60 +1/60 +1/60 +1/60 +1/60 +1/120
Слайд 5
Следующий шаг сделали древние греки, которые свели математику

к геометрическим построениям. Это было, по тем временам, очень
наглядно. Развел ножки циркуля, отложил отрезок пять раз. Затем его же – семь раз. И сразу видно, какой насколько больше. Расположил отрезки параллельно на определенном расстоянии, провел прямые через их концы – видно, какой угол получился. Греки работали с обыкновенными дробями не часто, поэтому использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятеричным дробям.
Недостатки греческой системы счисления относят к их любви к строгости, которое заметно увеличило трудности, связанные с анализом отношения несоизмеримых величин. Слово «число» греки понимали как набор единиц, поэтому то, что мы теперь рассматриваем как единое число – дробь, – греки понимали как отношение двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике.
Современному человеку, даже специалисту, трудно представить себе такую математику, поэтому многие грандиозные сооружения и замечательные машины древности приписываются сегодня то ли инопланетянам, то ли атлантам, то ли еще кому-то, кроме тех людей, которые их на самом деле сделали.
Геометризация математики позволяла сравнивать без какого-либо выделенного эталона любые числа, делятся они друг на друга или нет. Поэтому дроби стали простыми: 3/11; 123/768 и т.п.
До поры, до времени, пока для практики не требовались очень большие и очень малые числа, простые дроби были вне конкуренции.
Слайд 6
Революцию в математике произвели не позднее V в.
н. э. индийцы, придумав отдельные значки для цифр: 0,
1, 2, 3, 4, 5, 6, 7, 8, 9. Они шли от того же счета на пальцах, поэтому и значков придумали 10, а не 12 или 60. Достаточно удобно – два простых делителя, 2 и 5 – и без труда может запомнить любой. 12 (дюжина) перед 10 не имеет преимущества, т.к. у него тоже два простых делителя: 2 и 3, а значков для записи требуется на два больше.
Слайд 7
Индийские цифры позволяли записывать любое, сколь угодно большое
число в т. наз. позиционной системе. Каждая цифра слева
от предыдущей считалась умноженной на 10. 458 = 4х10х10 + 5х10 + 8. 10 в таком случае – основание системы счисления. И оно же самым естественным образом становилось универсальным знаменателем дробей, вроде вавилонского 60, но доступным обычному уму.
Появление позиционной системы во многом способствовало прогрессу науки и техники. Геометрия циркуля и линейки тут выдохлась – ее точность была ограниченной. А математика становилась все более изощренной и оперировала все более абстрактными понятиями.
Есть ли у простых дробей будущее? Казалось бы, нет. Куда там, если даже десятичные отступают под натиском процентов.
Слайд 9
Дроби в Древнем Риме
У римлян основной единицей измерения
массы, а также и денежной единицей служил «асс». Асс
делился на 12 равных частей - унций. Из них складывали все дроби со знаменателем 12, то есть 1/12, 2/12, 3/12… Со временем унции стали применяться для измерения любых величин.
Так возникли римские двенадцатеричные дроби, то есть дроби, у которых знаменателем всегда было число 12. Вместо 1/12 римляне говорили «одна унция».
Сейчас иногда говорят: «скрупулёзно изучен этот вопрос». Это значит, что вопрос изучен до конца, что ни одной самой малой неясности не осталось. А происходит странное слово «скрупулёзно» от римского названия 1/288 асса – «скрупулус».
Слайд 10
Дроби в Древнем Египте
На протяжении многих веков египтяне
именовали дроби «ломаным числом», а первая дробь, с которой
они познакомились, была 1/2 . За ней последовали 1/4, 1/8 , 1/16, … затем 1/3, 1/6, … т.е. самые простые дроби, называемые единичными или основными дробями.
У них числитель всегда единица. Лишь значительно позже у греков, затем у индийцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В Древнем Египте архитектура достигла высокого развития. Чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.
Слайд 11
Дроби в Древнем Китае
В Древнем Китае уже пользовались
десятичной системой мер, обозначали дробь словами, используя меры длины
чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзу-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Слайд 12
Дроби на Руси
В русском языке слово «дробь» появилось
лишь в VIII веке. Происходит оно от слова «дробить,
разбивать, ломать на части». В русских рукописных арифметиках XVII в. дроби называли долями, позднее «ломаными числами». В старых руководствах существуют следующие названия дробей на Руси:
1/2 - половина, полтина 1/3 – треть
1/4 – четь 1/6 – полтреть
1/8 – полчеть 1/12 –полполтреть
1/16 – полполчеть 1/24 – полполполтреть (малая треть)
1/32 – полполполчеть (малая четь) 1/5 – пятина
1/7 – седьмина 1/10 - десятина
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.
Русский термин ДРОБЬ, как и его аналоги в других языках, происходят от латинского FRACTURA, который означает ломать, раздроблять.
Слайд 13
Дроби в других государствах древности
В китайской «Математике в

девяти разделах» уже имеют место сокращения дробей и все
действия с дробями. У индийского математика Брахмагупты найдена достаточно развитую систему дробей. У него встречаются разные дроби: и основные, и производные с любым числителем. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной черты, а просто размещаются один над другим.
Арабы первыми начали отделять чертой числитель от знаменателя.
Леонардо Пизанский уже записывает дроби, помещая в случае смешанного числа, целое число справа, но читает так, как принято у нас. В XV – XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках.
Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.