- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Двугранный угол, решение задач
Содержание
- 2. Цель урока:Сформировать у обучающихся конструктивный подход по выработке умений и навыков находить угол между плоскостями.
- 3. Вид урока: изучение и первичное закрепление новых
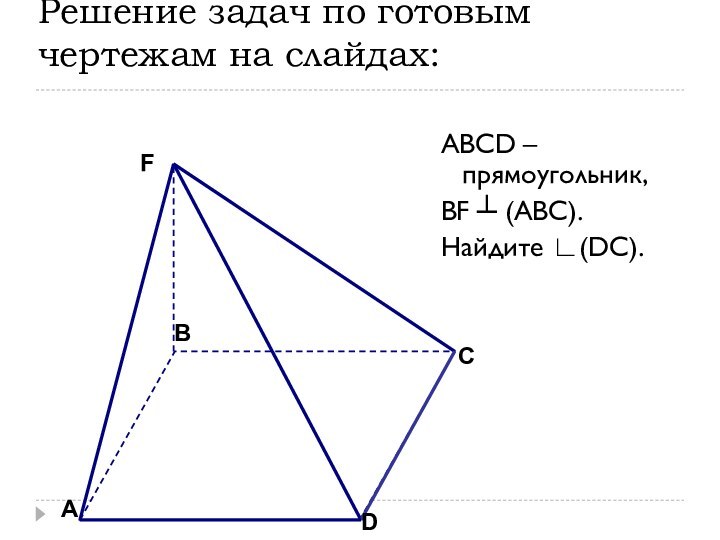
- 4. Решение задач по готовым чертежам на слайдах:ABCD – прямоугольник, BF ┴ (ABC).Найдите ∟(DC).АDCBF
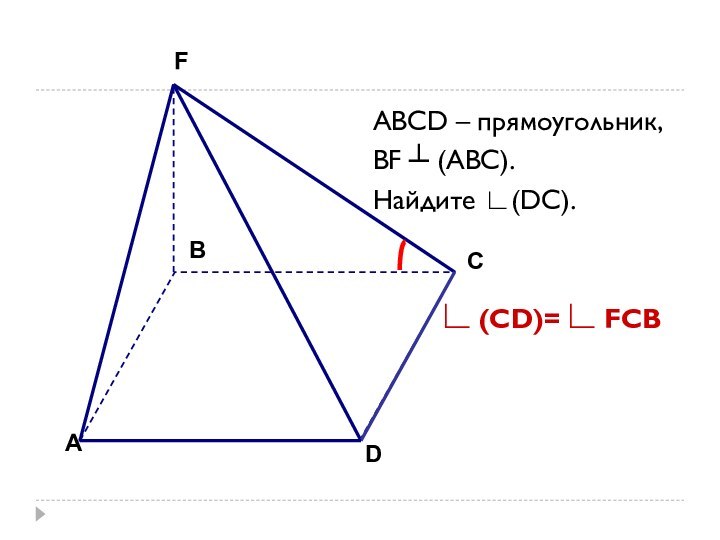
- 5. ABCD – прямоугольник, BF ┴ (ABC).Найдите ∟(DC). ∟ (СD)= ∟ FCBАDCBF
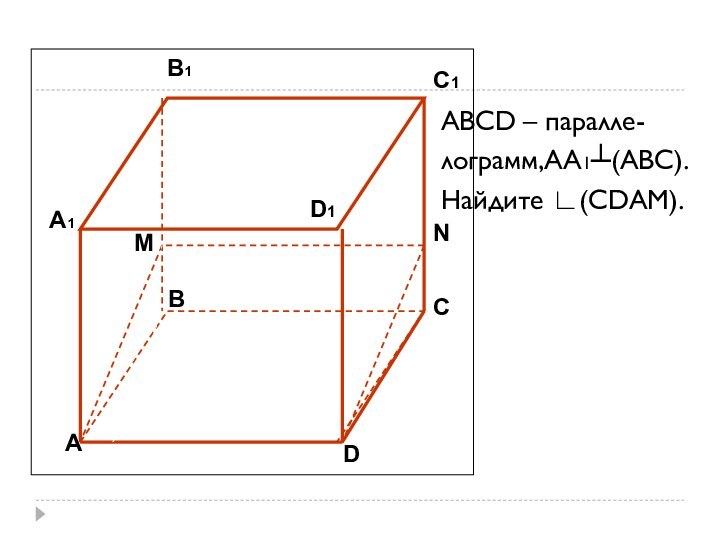
- 6. АА1СС1В1DD1BNMABCD – паралле-лограмм,АА1┴(ABC).Найдите ∟(СDАМ).
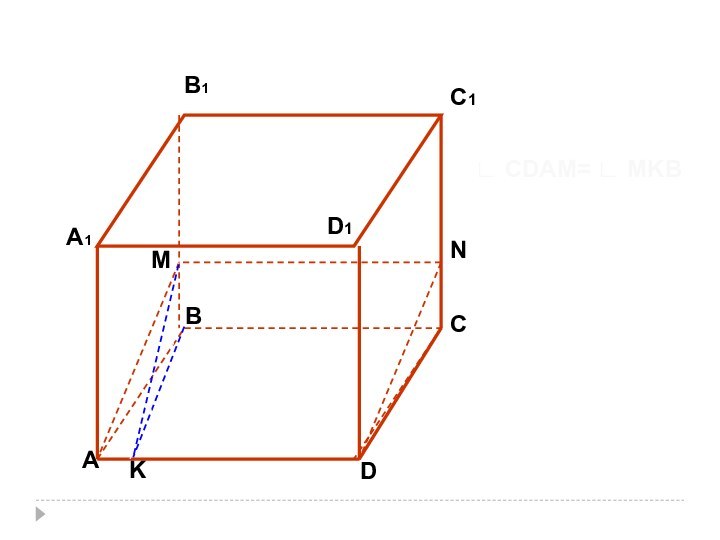
- 7. АА1СС1В1DD1BNMK∟ CDAM= ∟ MKB
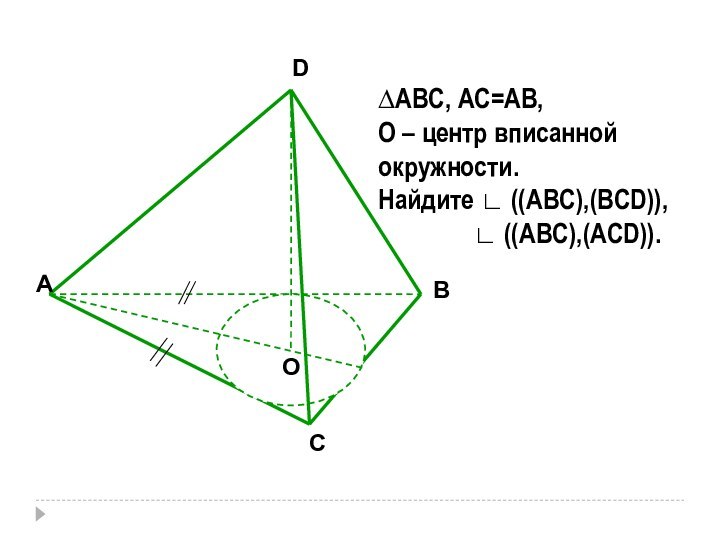
- 8. АСВDО∆АВС, АС=АВ,О – центр вписанной окружности.Найдите ∟
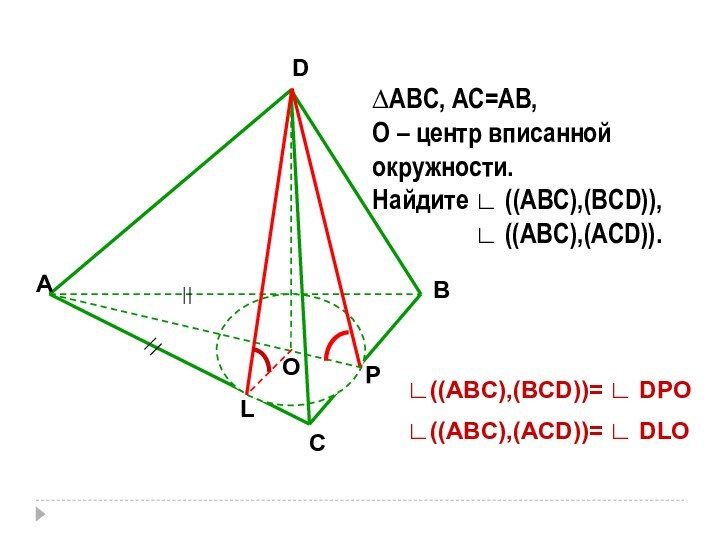
- 9. АСВDО∆АВС, АС=АВ,О – центр вписанной окружности.Найдите ∟
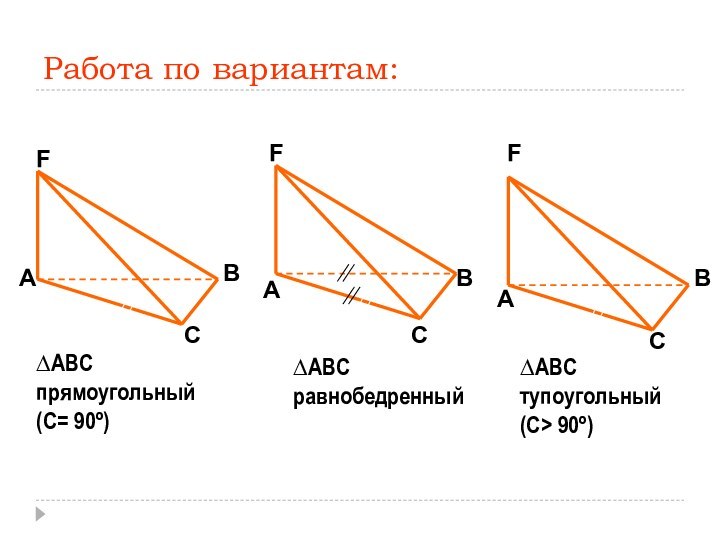
- 10. АСВАСВАСВFFF∆АВСпрямоугольный(С= 90º)∆АВСравнобедренный∆АВСтупоугольный(С> 90º)Работа по вариантам:
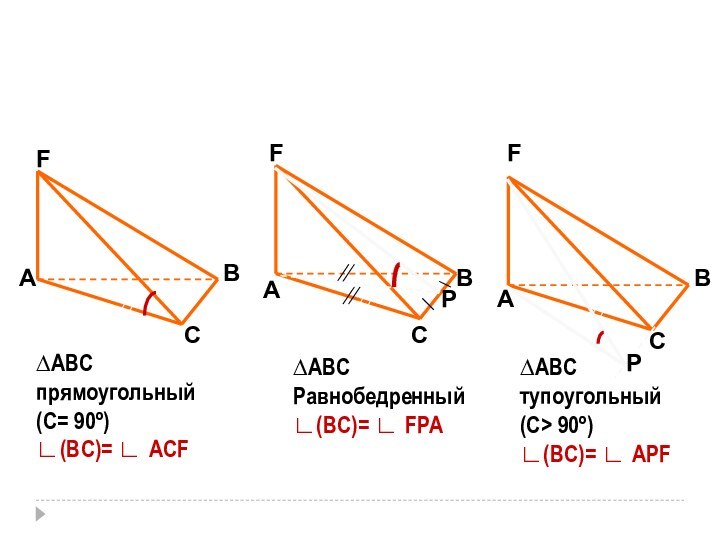
- 11. АСВАСВАСВFFF∆АВСпрямоугольный(С= 90º)∟(BC)= ∟ ACF∆АВСРавнобедренный∟(BC)= ∟ FPA∆АВСтупоугольный(С> 90º)∟(BC)= ∟ APFРР
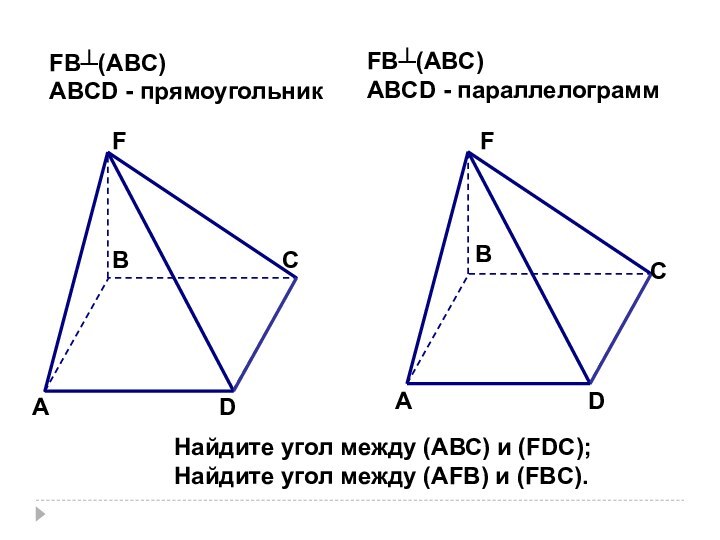
- 12. АDСВFFADBCFB┴(ABC)ABCD - прямоугольникFB┴(ABC)ABCD - параллелограммНайдите угол между (АВС) и (FDC);Найдите угол между (AFB) и (FBC).
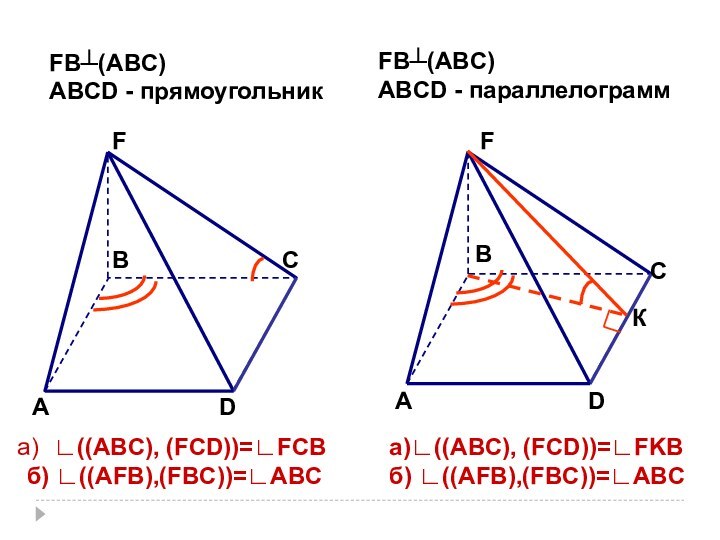
- 13. АDСВFFADBCFB┴(ABC)ABCD - прямоугольникFB┴(ABC)ABCD - параллелограмм∟((ABC), (FCD))=∟FCBб) ∟((AFB),(FBC))=∟ABCКа)∟((ABC), (FCD))=∟FKBб) ∟((AFB),(FBC))=∟ABC
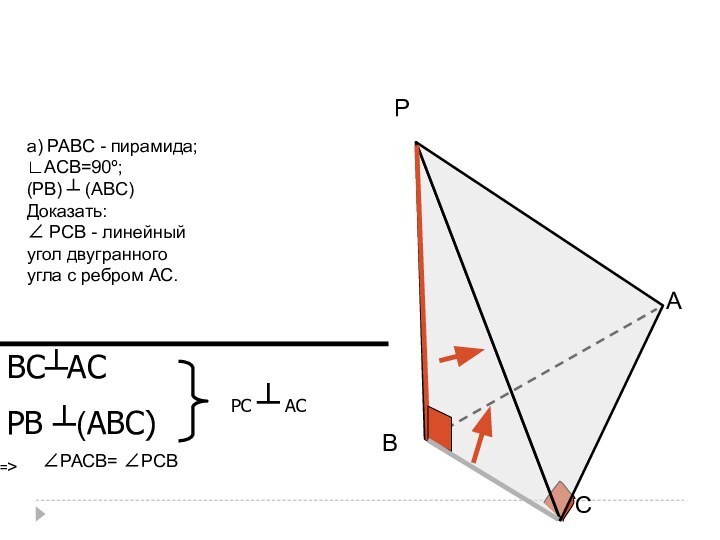
- 14. а) РАВС - пирамида;∟АСВ=90º;(РВ) ┴ (АВС)Доказать:∠
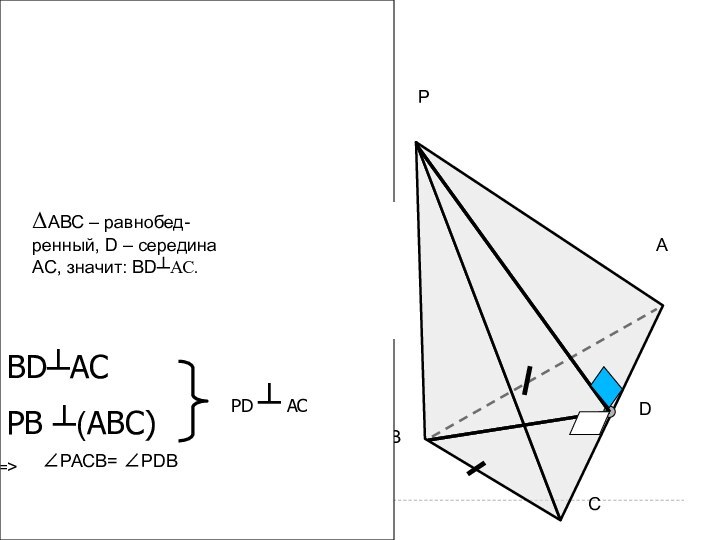
- 15. в) РАВС - пирамиDа;АВ=ВС; D- сереDина
- 16. с) РАВСD - пирамида;(РВ) ┴ (АВС);(ВК)
- 17. а) РАВС - пирамида;основание - правильныйтреугольник;Какой
- 18. в) Построить линейный угол двугранного
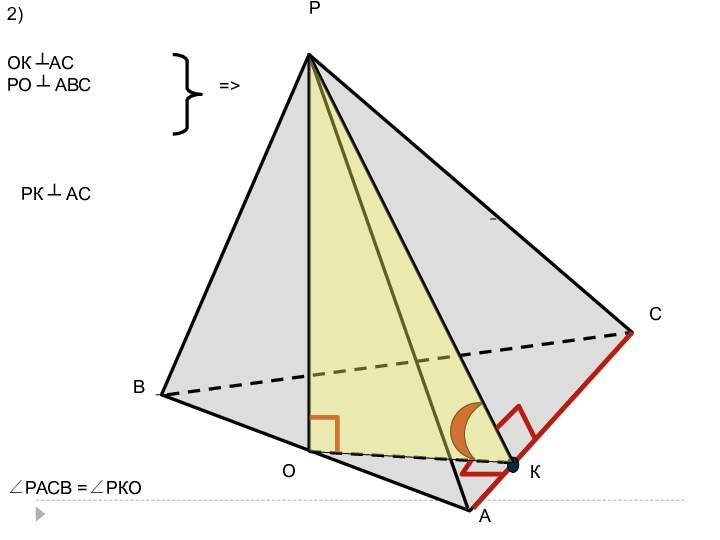
- 19. РАСВОКВК-медиана,=>ВО ┴АСРО ┴ АВС=>РК ┴ АСΔАВС-правильныйВК - высота∠РАСВ =∠РКВ
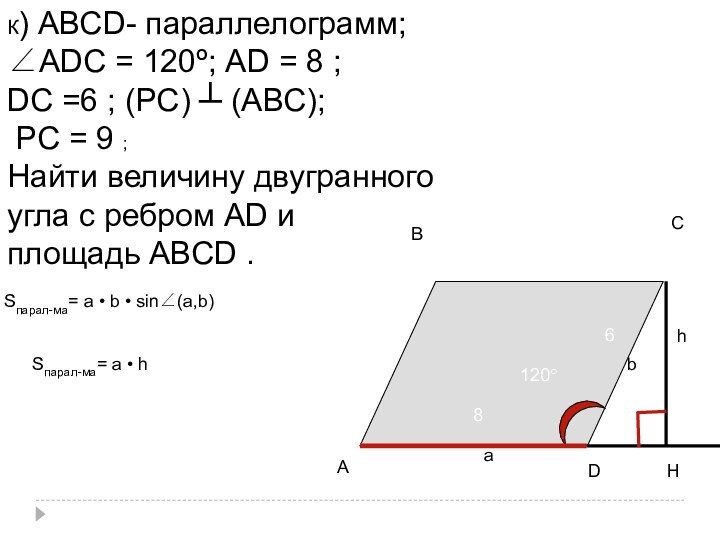
- 20. с) Построить линейный угол двугранного угла с
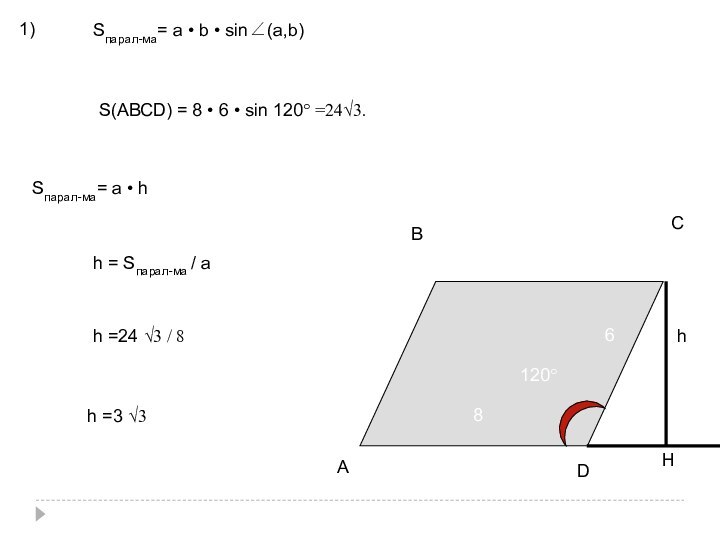
- 21. АСРВОНКАВ=ВС=>КО ┴АСРО ┴ АВС=>КР ┴ АСВН ┴АСКО║ВН∠РАСВ =∠РКО
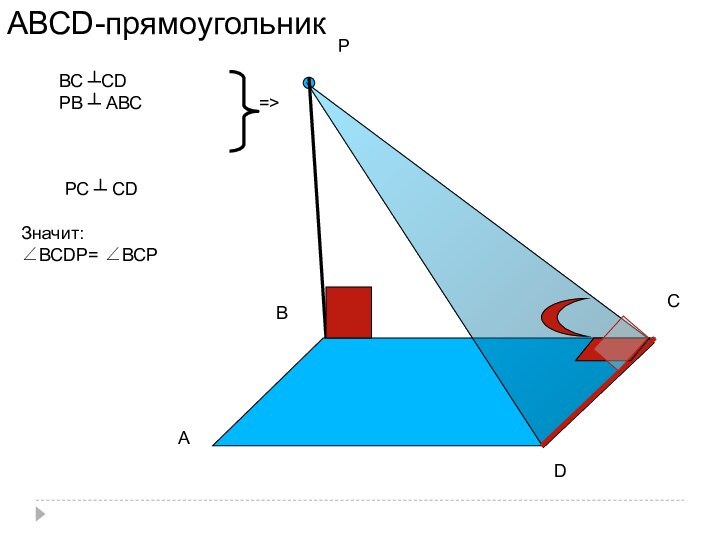
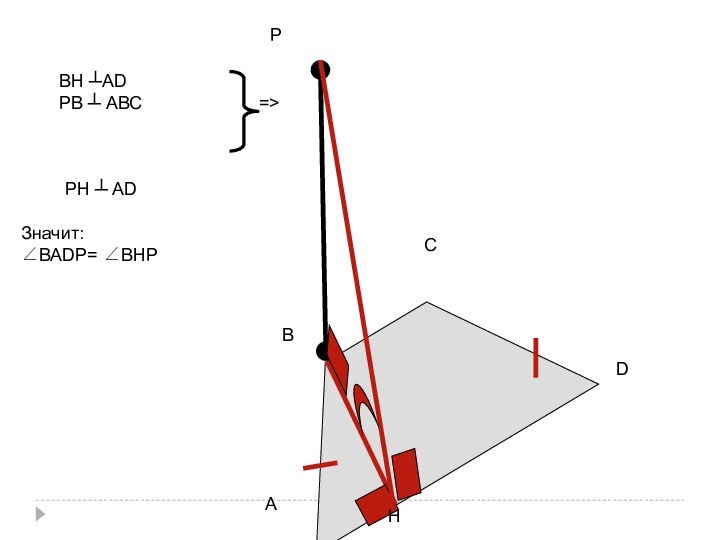
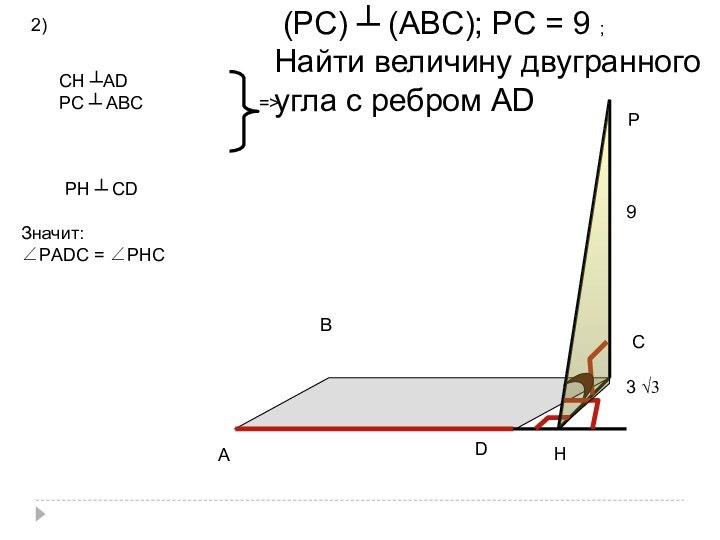
- 22. D) Дан прямоугольник АВСD и точка Р
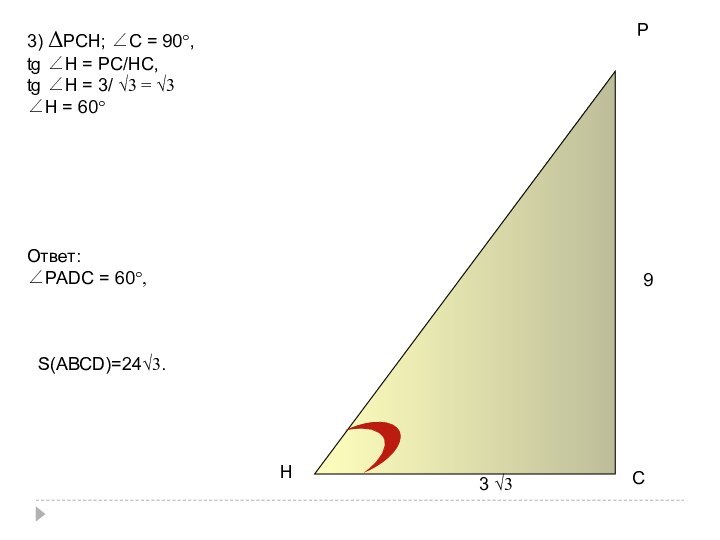
- 23. АРDСВВС ┴СDРВ ┴ АВС=>РС ┴ СDЗначит:∠ВСDР= ∠ВСРАВСD-прямоугольник
- 24. ОͼАВ; (РО) ┴ (АВС).е)Дан прямоугольник АВСD и
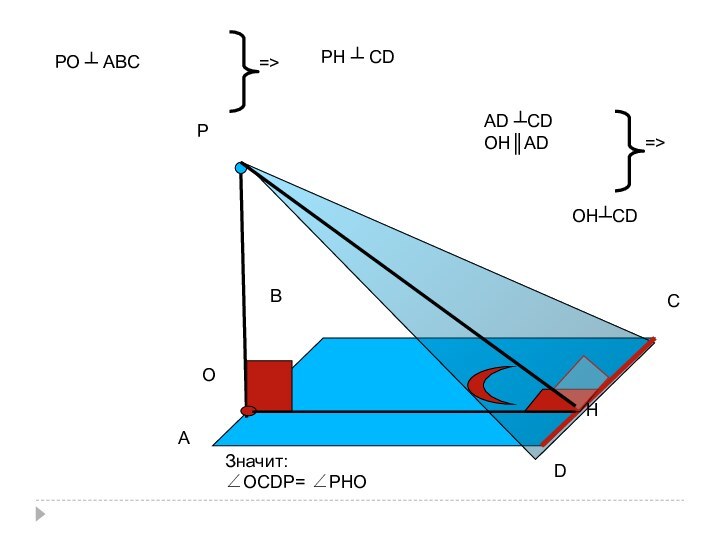
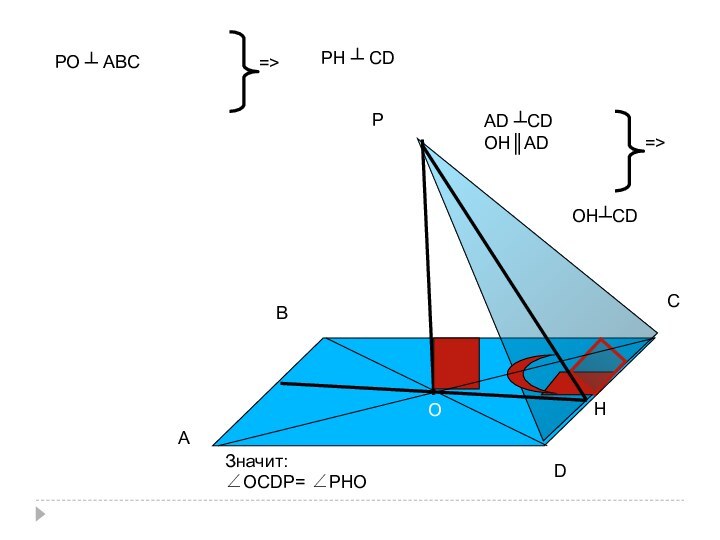
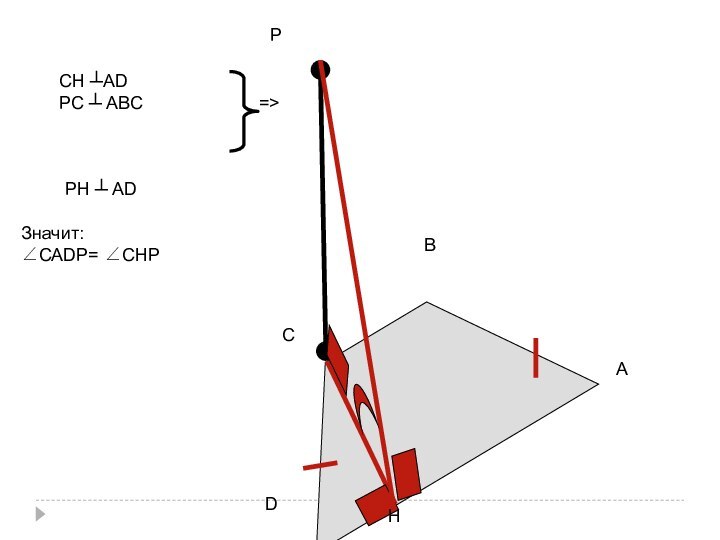
- 25. АРDСВОНЗначит:∠ОСDР= ∠РНОРО ┴ АВС=>РН ┴ СDАD ┴СD ОН║АDОН┴СD=>
- 26. О – точка пересечения диагоналей АВСD, (РО)
- 27. АРDСВОНАD ┴СD ОН║АDОН┴СD=>Значит:∠ОСDР= ∠РНОРО ┴ АВС=>РН ┴ СD
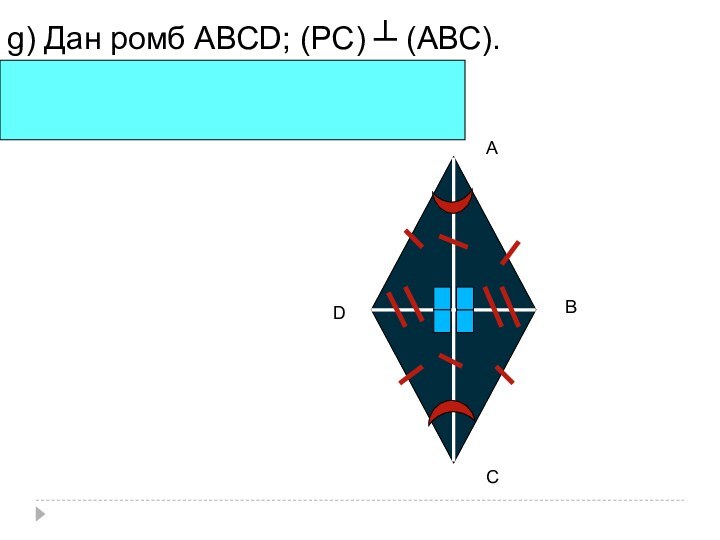
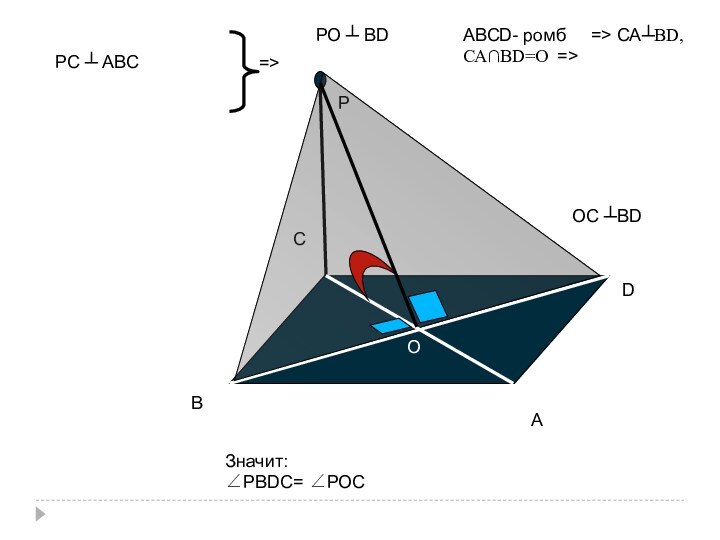
- 28. g) Дан ромб АВСD; (РС) ┴ (АВС).Построить линейный угол двугранного угла с ребром ВD. СВАD
- 29. РСВDААВСD- ромб => СА┴ВD, СА∩ВD=О => ОС ┴ВDЗначит:∠РВDС= ∠РОСРС ┴ АВС=>РО ┴ ВDО
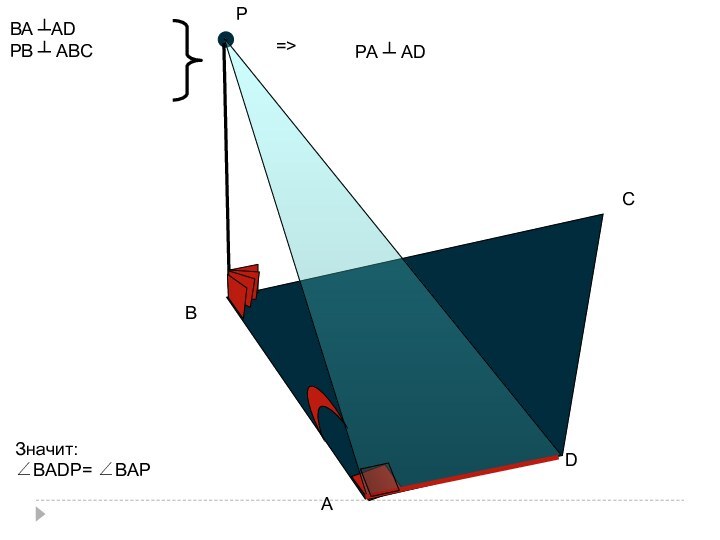
- 30. i) Дана трапеция АВСD; ∠ВАD=90º;Построить линейный угол
- 31. РDВСАВА ┴АDРВ ┴ АВС=>РА ┴ АDЗначит:∠ВАDР= ∠ВАР
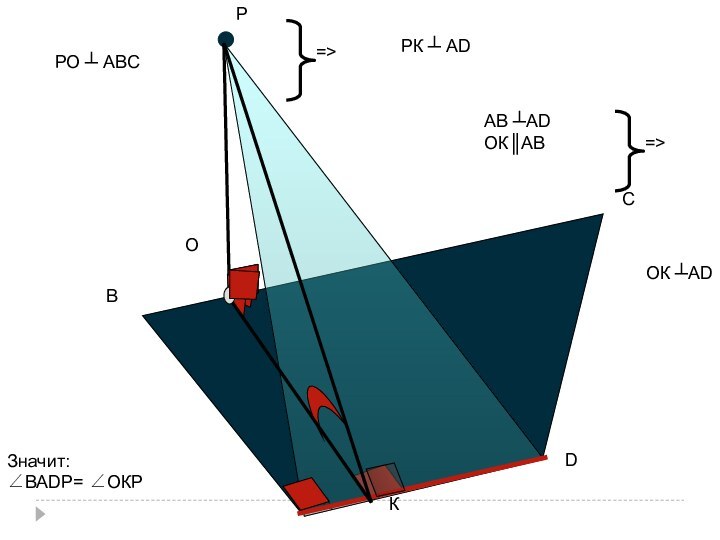
- 32. k) Dана трапеция АВСD; ∠ВАD=90º;Построить линейный угол
- 33. РDВСАЗначит:∠ВАDР= ∠ОКРОКАВ ┴АD ОК║АВОК ┴АD=>РО ┴ АВС=>РК ┴ АD
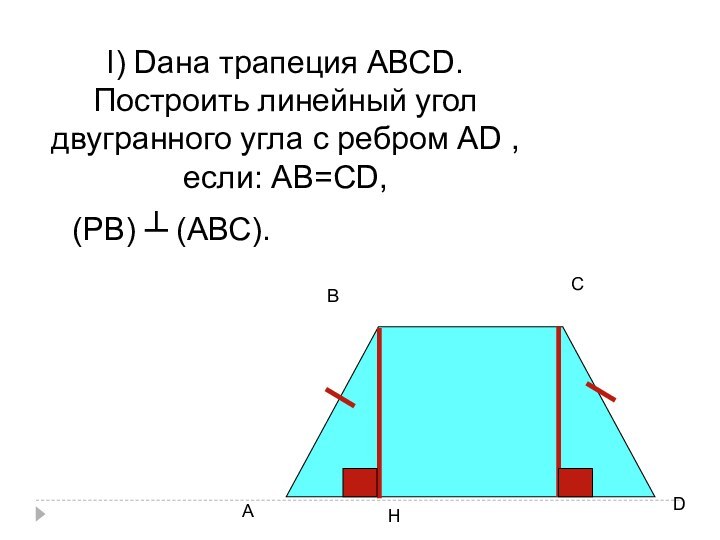
- 34. l) Dана трапеция АВСD.Построить линейный угол двугранного
- 35. ВDСАНРВН ┴АDРВ ┴ АВС=>РН ┴ АDЗначит:∠ВАDР= ∠ВНР
- 36. АВСD — равнобокая трапеция; АВ=СD, (РС) ┴
- 37. САВDНРСН ┴АDРС ┴ АВС=>РН ┴ АDЗначит:∠САDР= ∠СНР
- 38. Вычислительные задачи.
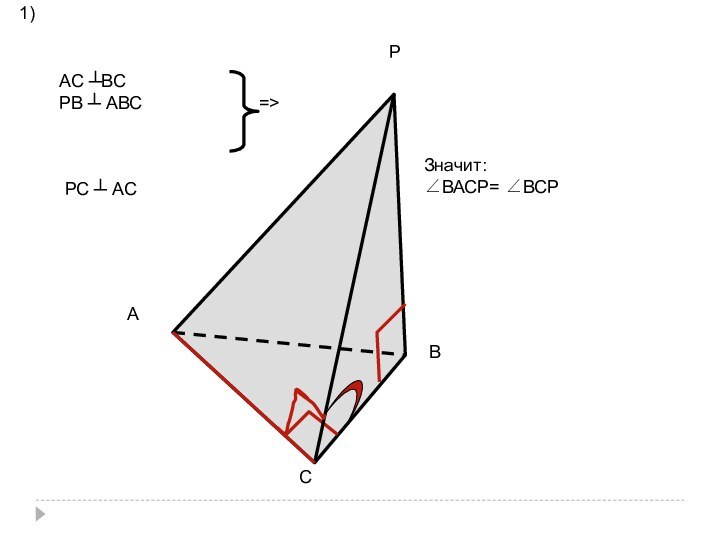
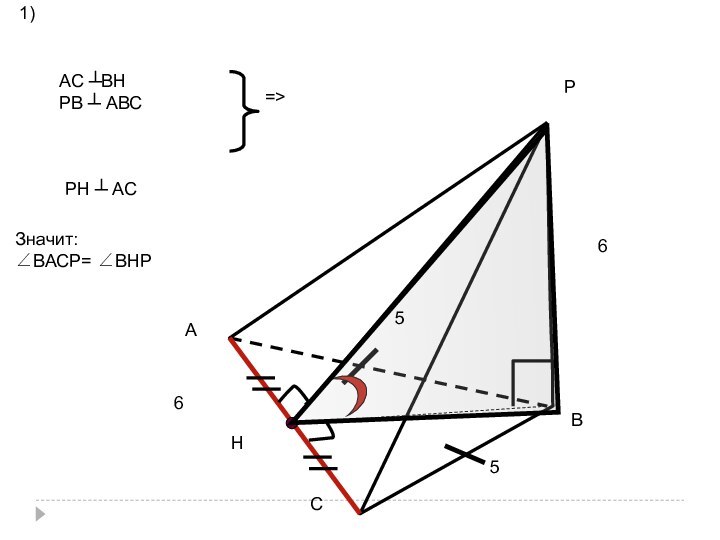
- 39. а) РАВС — пирамида; найти величину двугранного
- 40. АСРВАС ┴ВСРВ ┴ АВС=>РС ┴ АСЗначит:∠ВАСР= ∠ВСР1)
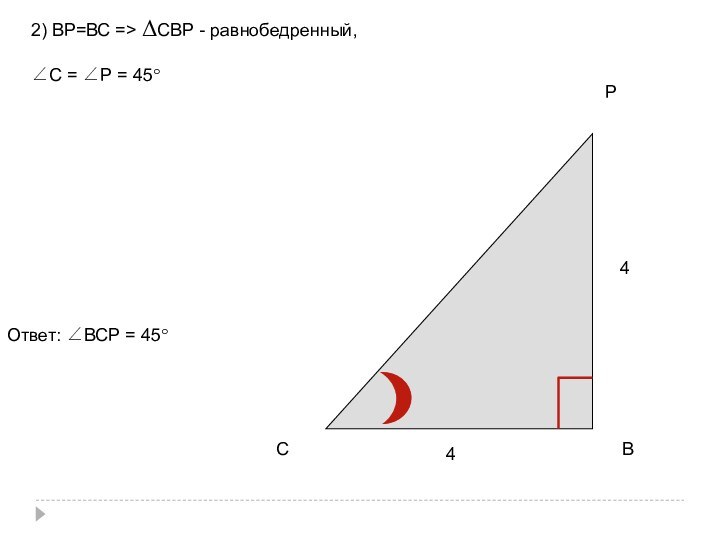
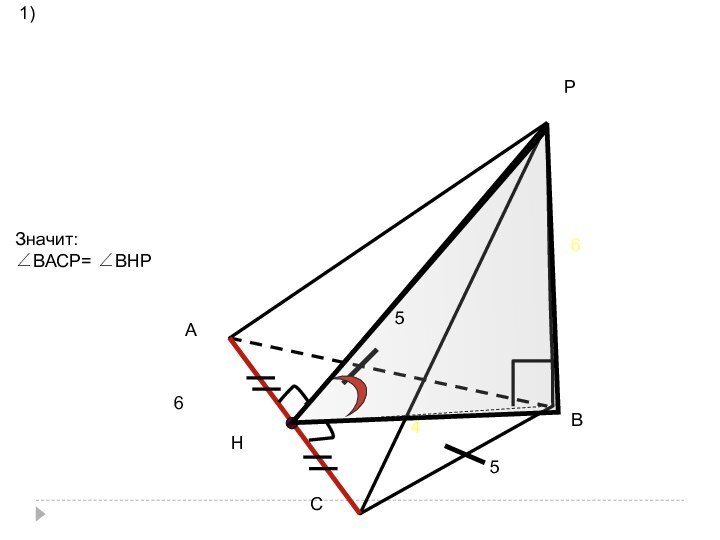
- 41. СВР442) ВР=ВС => ΔСВР - равнобедренный,∠С = ∠Р = 45°Ответ: ∠ВСР = 45°
- 42. в) РАВС — пирамида; найти величину двугранного
- 43. РАВСНАС ┴ВНРВ ┴ АВС=>РН ┴ АСЗначит:∠ВАСР= ∠ВНР1)55666
- 44. АВСН556332)ΔАВС -равнобедренный, ВН - высота,значит: ВН- медиана, АН=НС=3,ΔВНС - прямоугольный,ВН2=ВС2-НС2,ВН=4
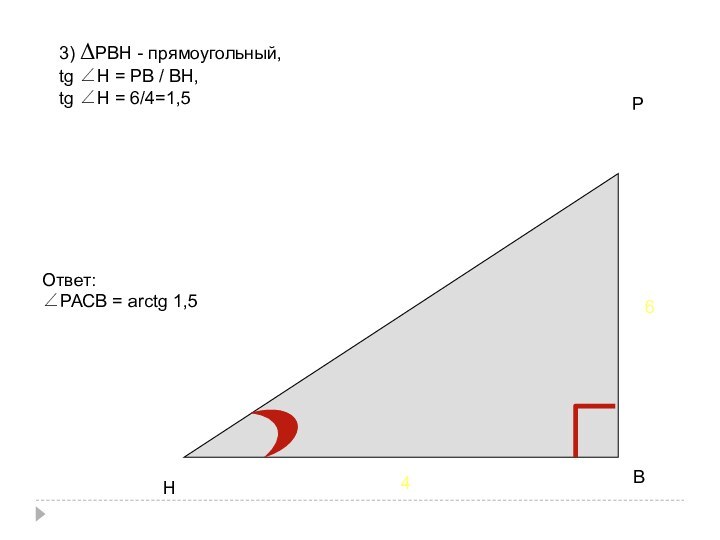
- 45. РАВСНЗначит:∠ВАСР= ∠ВНР1)556664
- 46. РНВ463) ΔРВН - прямоугольный,tg ∠Н = РВ / ВН,tg ∠Н = 6/4=1,5Ответ:∠РАСВ = arctg 1,5
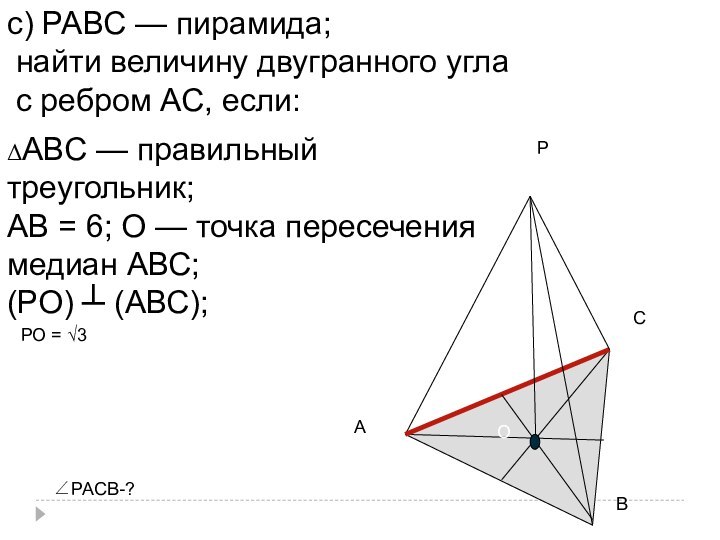
- 47. с) РАВС — пирамида; найти величину двугранного
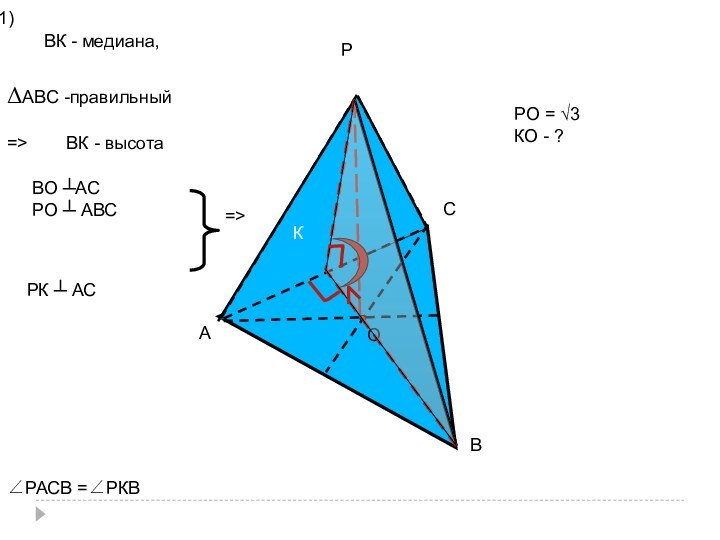
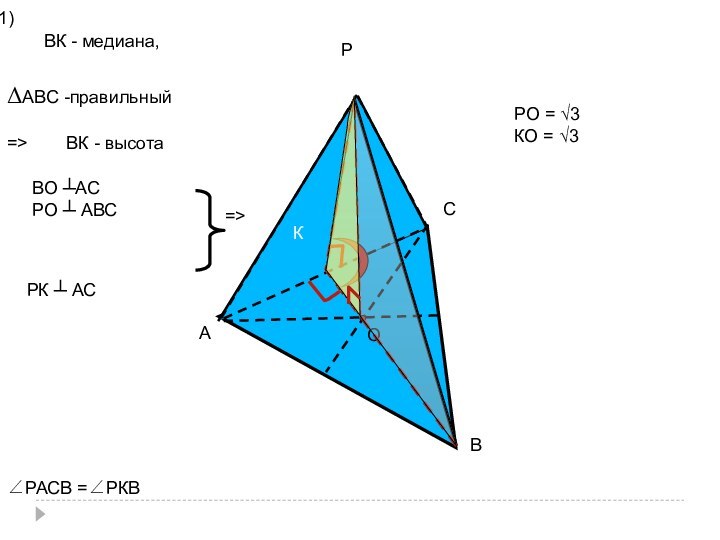
- 48. РАСВОКВК - медиана,=>ВО ┴АСРО ┴ АВС=>РК ┴ АСΔАВС -правильныйВК - высота∠РАСВ =∠РКВ1)РО = √3КО - ?
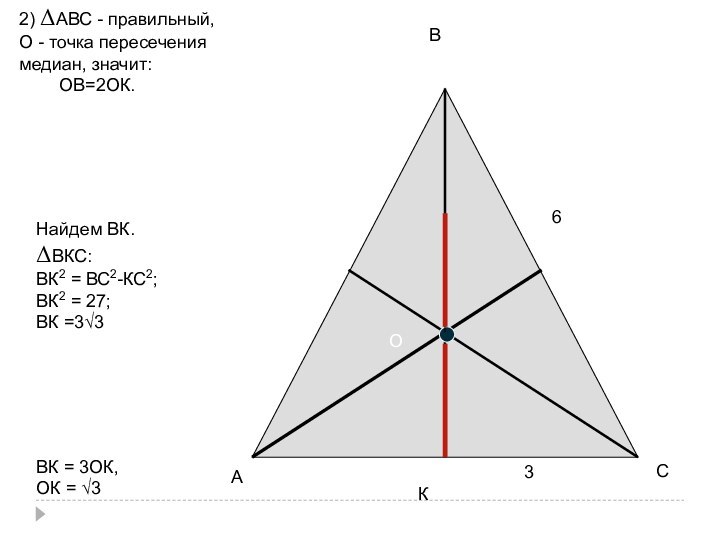
- 49. СВКОА2) ΔАВС - правильный,О - точка пересечения
- 50. РАСВОКВК - медиана,=>ВО ┴АСРО ┴ АВС=>РК ┴ АСΔАВС -правильныйВК - высота∠РАСВ =∠РКВ1)РО = √3КО = √3
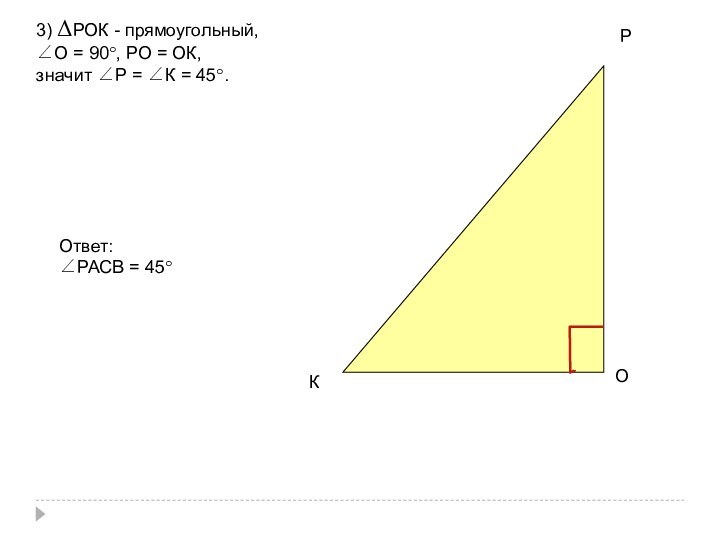
- 51. 3) ΔРОК - прямоугольный, ∠О = 90°,
- 52. D) РАВС — пирамида; найти величину двугранного
- 53. АСВОНК1) ВН - высотаправильного ΔАВС, ВН┴АСОК║ВН=>ОК┴АС
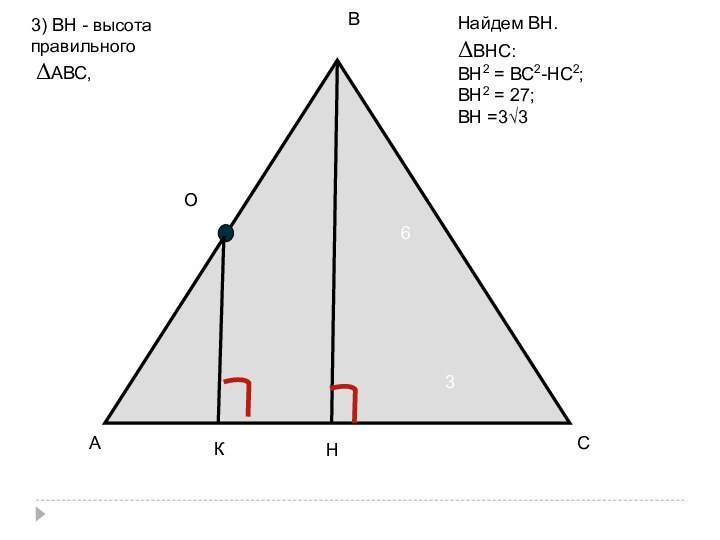
- 54. ВАСРОКОК ┴АСРО ┴ АВС=>РК ┴ АС∠РАСВ =∠РКО2)
- 55. АСВОНК3) ВН - высотаправильного ΔАВС, 6Найдем ВН.ΔВНС:ВН2 = ВС2-НС2;ВН2 = 27;ВН =3√33
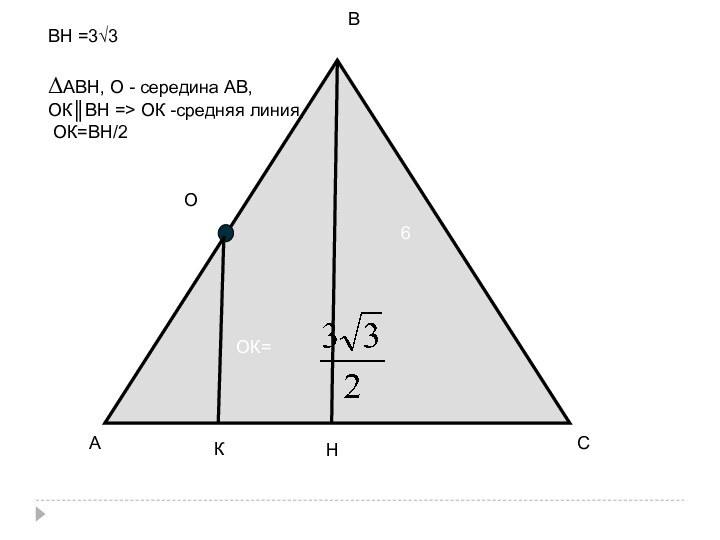
- 56. АСВОНК6ВН =3√3ΔАВН, О - середина АВ, ОК║ВН => ОК -средняя линия, ОК=ВН/2ОК=
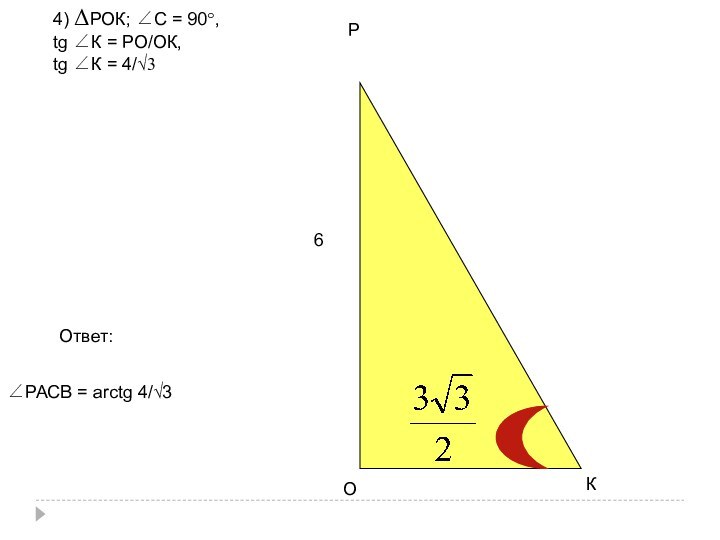
- 57. ОКР64) ΔРОК; ∠С = 90°, tg ∠К
- 58. е) АВСD — прямоугольник; ВD = 4√3
- 59. ВРАСD1) ∠РDСВ=60°ВС ┴СDРВ ┴ АВС=>РС ┴ СDЗначит:∠РDСВ
- 60. ВРС660°2) ΔРВС, ∠В = 90°, tg ∠С
- 61. ВРАСDВD = 4√3 ;РВ = 6 ;∠РСВ = 60°660°4√32√3
- 62. ВСD4√32√33) ΔВСD; ∠С = 90°,СD2 = ВD2
- 63. f) АВСD — прямоугольник; площадь АВСD равна
- 64. ВРАСD64∠РDСВ - ?1)ВС ┴СDРВ ┴ АВС=>РС ┴ СDЗначит:∠РDСВ = ∠РСВ S(АВСD)=48,РВ = 6,СD = 4.
- 65. 2) АВСD - прямоугольникS(АВСD) = АВ•ВС =
- 66. ВРАСD6123) ΔРВС; ∠В = 90°,tg ∠С = РВ/ВС,tg ∠С = 0,5Ответ:∠РDСВ = arctg 0,5
- 67. g) АВСD — ромб;ВD = 4 ;
- 68. (РС) ┴ (АВС); РС = 8 ;Двугранный
- 69. 45°РОС83) ΔРСО; ∠С = 90°, ∠О =
- 70. АВСDSромба =d1 • d2:2 d1d244) d1 =
- 71. К) АВСD- параллелограмм;∠АDС = 120º; АD =
- 72. 1)АВС8120°6hSпарал-ма= a • b • sin∠(a,b)S(АВСD) =
- 73. 2)ABCDPH (РС) ┴ (АВС); РС = 9
- 74. 93 √3PCH3) ΔРCH; ∠C = 90°,tg ∠H
- 75. Задача №2 (а)Ребро - TM, грани: PTM,
- 76. Задача №2 (в)Ребро - KT, грани: PKT,
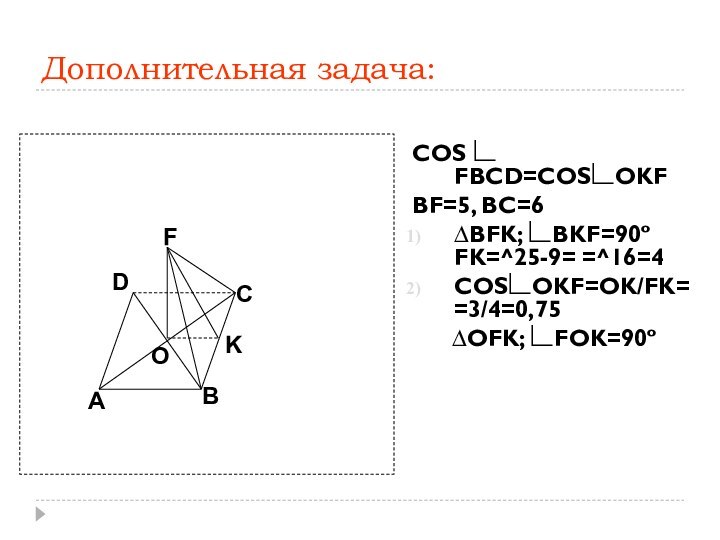
- 77. Дополнительная задача:COS ∟ FBCD=COS∟OKFBF=5, BC=6∆BFK; ∟BKF=90º FK=^25-9=
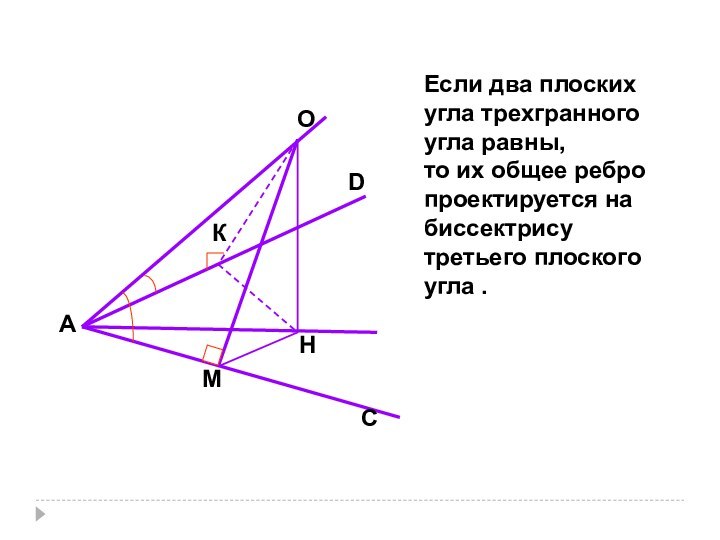
- 78. AМСHКODЕсли два плоских угла трехгранного угла равны,то их общее ребро проектируется на биссектрисутретьего плоского угла .
- 79. Решение задач: Боковая поверхность треугольной пирамиды
- 80. Проверка:L,B,Y;B=L+П/3; Y=B+П/3=L+2П/3YП/3, но B=L+П/3>2П/3;Y=L+2П/3>П/3+2П/3Вывод: такого угла не существует.
- 81. Дополнительная задача: Все грани параллелепипеда равные
- 82. Скачать презентацию
- 83. Похожие презентации
Цель урока:Сформировать у обучающихся конструктивный подход по выработке умений и навыков находить угол между плоскостями.
Слайд 2
Цель урока:
Сформировать у обучающихся конструктивный подход по выработке
умений и навыков находить угол между плоскостями.
Слайд 3
Вид урока: изучение и первичное закрепление новых знаний
Оборудование: компьютер, проектор, слайды, чертежные инструменты, цветные мелки.
Слайд 4
Решение задач по готовым чертежам на слайдах:
ABCD –
прямоугольник,
BF ┴ (ABC).
Найдите ∟(DC).
А
D
C
B
F
Слайд 9
А
С
В
D
О
∆АВС, АС=АВ,
О – центр вписанной
окружности.
Найдите ∟ ((АВС),(ВСD)),
∟ ((ABC),(ACD)).
P
L
∟((ABC),(BCD))=
∟ DPO∟((ABC),(ACD))= ∟ DLO
Слайд 10
А
С
В
А
С
В
А
С
В
F
F
F
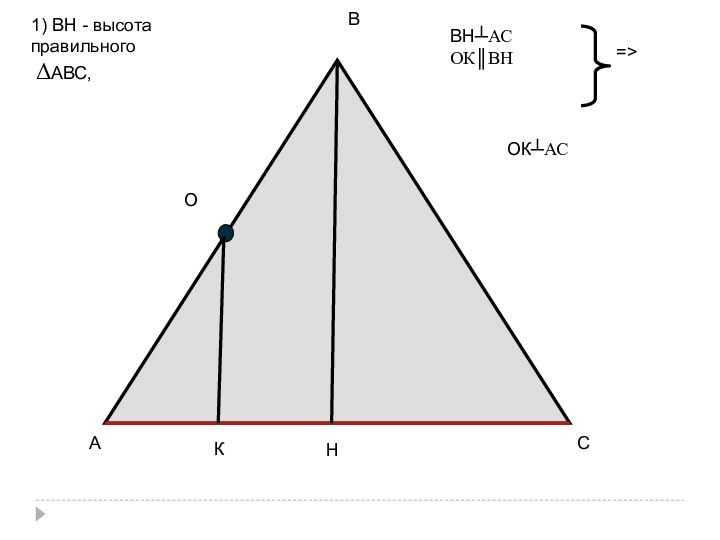
∆АВС
прямоугольный
(С= 90º)
∆АВС
равнобедренный
∆АВС
тупоугольный
(С> 90º)
Работа по вариантам:
Слайд 11
А
С
В
А
С
В
А
С
В
F
F
F
∆АВС
прямоугольный
(С= 90º)
∟(BC)= ∟ ACF
∆АВС
Равнобедренный
∟(BC)= ∟ FPA
∆АВС
тупоугольный
(С> 90º)
∟(BC)= ∟
APF
Р
Р
Слайд 12
А
D
С
В
F
F
A
D
B
C
FB┴(ABC)
ABCD - прямоугольник
FB┴(ABC)
ABCD - параллелограмм
Найдите угол между (АВС)
и (FDC);
Найдите угол между (AFB) и (FBC).
Слайд 13
А
D
С
В
F
F
A
D
B
C
FB┴(ABC)
ABCD - прямоугольник
FB┴(ABC)
ABCD - параллелограмм
∟((ABC), (FCD))=∟FCB
б) ∟((AFB),(FBC))=∟ABC
К
а)∟((ABC), (FCD))=∟FKB
б)
∟((AFB),(FBC))=∟ABC
Слайд 14
а) РАВС - пирамида;
∟АСВ=90º;
(РВ) ┴ (АВС)
Доказать:
∠ РСВ -
линейный
угол двугранного
угла с ребром АС.
В
А
С
Р
ВС┴АС
РВ ┴(АВС)
РС ┴
АС=>
∠РАСВ= ∠РСВ
Слайд 15
в) РАВС - пирамиDа;
АВ=ВС; D- сереDина АС;
(РВ) ┴
(АВС);
Dоказать:
∟РDВ - линейный
угол Dвугранного
угла с ребром АС.
В
Р
А
С
D
ΔАВС
– равнобед-ренный, D – середина
АС, значит: ВD┴АС.
ВD┴АС
РВ ┴(АВС)
РD ┴ АС
=>
∠РАСВ= ∠РDВ
Слайд 16
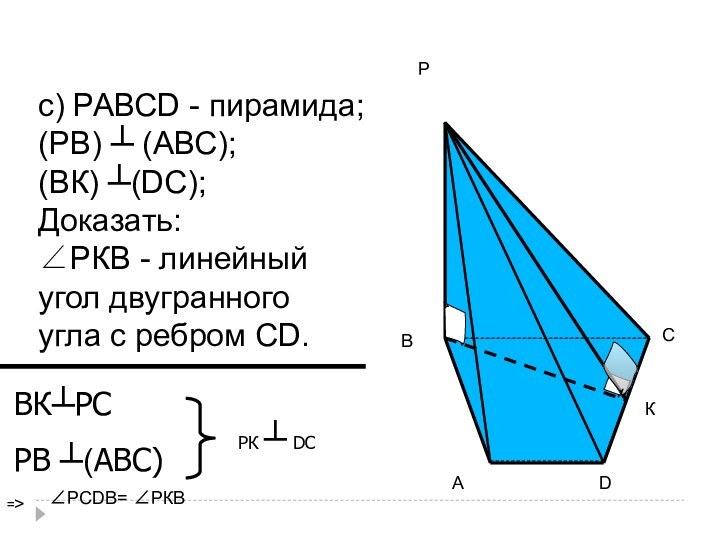
с) РАВСD - пирамида;
(РВ) ┴ (АВС);
(ВК) ┴(DС);
Доказать:
∠РКВ
- линейный
угол двугранного
угла с ребром СD.
А
В
D
С
Р
К
ВК┴РС
РВ ┴(АВС)
РК
┴ DС=>
∠РСDВ= ∠РКВ
Слайд 17
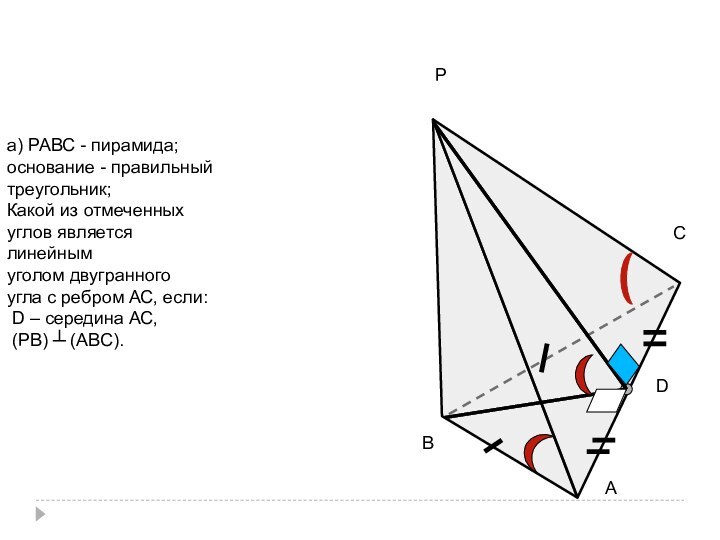
а) РАВС - пирамида;
основание - правильный
треугольник;
Какой из отмеченных
углов является
линейным
уголом двугранного
угла с ребром АС, если:
D – середина АС,(РВ) ┴ (АВС).
Р
D
С
В
А
Слайд 18
в) Построить линейный угол двугранного угла с ребром
АС,
если в пирамиде РАВС:
грань АВС – правильный
треугольник, О – точка пересечения медиан треугольника АВС, (РО) ┴ (АВС);∠РАСВ - ?
Слайд 20
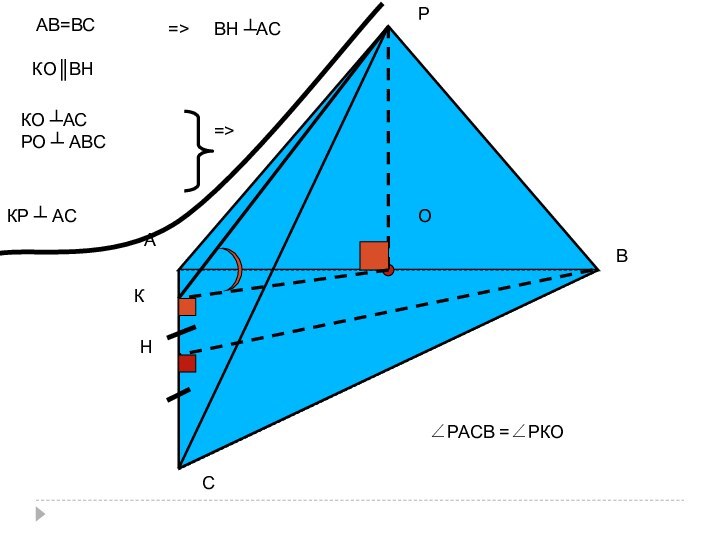
с) Построить линейный угол двугранного угла с
ребром
АС, если в
пирамиде РАВС:
грань АВС –
правильный
треугольник,О – середина АВ,
(РО) ┴ (АВС);
∠РАСО - ?
Слайд 22
D) Дан прямоугольник АВСD
и точка Р вне
его плоскости.
Построить линейный угол
двугранного угла с ребром DС,
если:(РВ) ┴ (АВС);
∠ВСDР - ?
Слайд 24
ОͼАВ; (РО) ┴ (АВС).
е)Дан прямоугольник АВСD
и точка
Р вне его плоскости.
Построить линейный угол
двугранного угла с
ребром DС, если:
∠ОСDР - ?
Слайд 26
О – точка пересечения
диагоналей АВСD,
(РО) ┴
(АВС).
f)Дан прямоугольник АВСD
и точка Р вне его плоскости.
Построить
линейный угол двугранного угла с ребром DС, если:
∠ОСDР - ?
Слайд 30
i) Дана трапеция АВСD; ∠ВАD=90º;
Построить линейный угол
двугранного
угла с ребром АD ,
если:
(РВ) ┴ (АВС).
С
D
А
В
АD║ВС
∠ВАDР -
?
Слайд 32
k) Dана трапеция АВСD;
∠ВАD=90º;
Построить линейный угол
двугранного
угла с
ребром АD , если:
О ВС; (РО)
┴ (АВС).
∠ВАDР - ?
Слайд 34
l) Dана трапеция АВСD.
Построить линейный угол
двугранного угла
с ребром АD ,
если: АВ=СD,
(РВ) ┴ (АВС).
А
D
С
В
Н
Слайд 36
АВСD — равнобокая трапеция; АВ=СD, (РС) ┴ (АВС);
m)
Dана трапеция АВСD.
Построить линейный угол
двугранного угла с ребром
АD , если:
Слайд 39
а) РАВС — пирамида;
найти величину двугранного угла
с ребром АС, если:
(РВ) ┴ (АВС); ∠АСВ = 90º;
ВС
= РВ = 4
Слайд 42
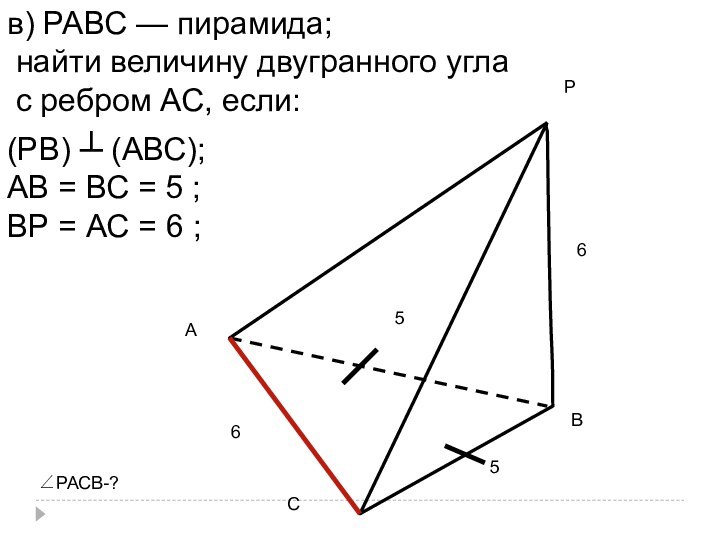
в) РАВС — пирамида;
найти величину двугранного угла
с ребром АС, если:
(РВ) ┴ (АВС);
АВ = ВС
= 5 ;ВР = АС = 6 ;
Р
А
В
С
5
5
6
6
∠РАСВ-?
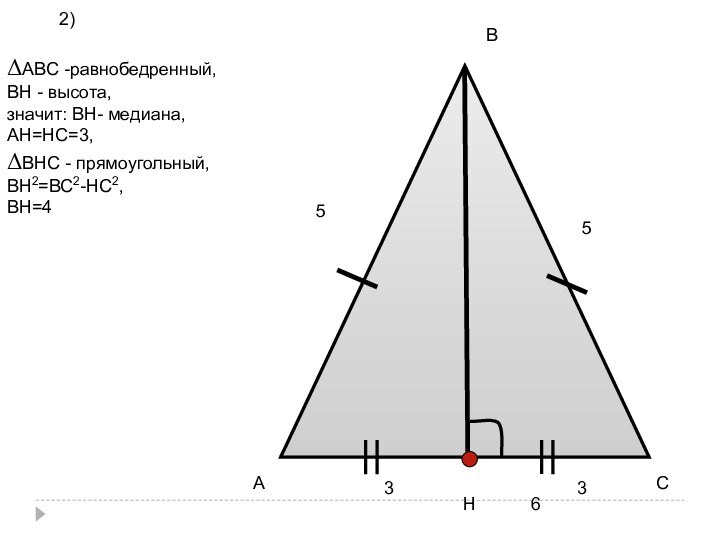
Слайд 44
А
В
С
Н
5
5
6
3
3
2)
ΔАВС -равнобедренный,
ВН - высота,
значит: ВН- медиана,
АН=НС=3,
ΔВНС
- прямоугольный,
ВН2=ВС2-НС2,
ВН=4
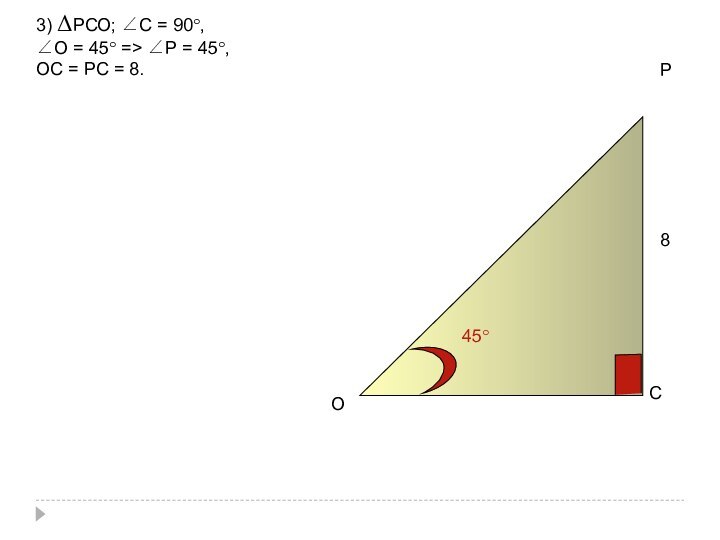
Слайд 47
с) РАВС — пирамида;
найти величину двугранного угла
с ребром АС, если:
ΔАВС — правильный треугольник;
АВ = 6;
О — точка пересечения медиан АВС;
(РО) ┴ (АВС);
А
О
Р
В
С
РО = √3
∠РАСВ-?
Слайд 48
Р
А
С
В
О
К
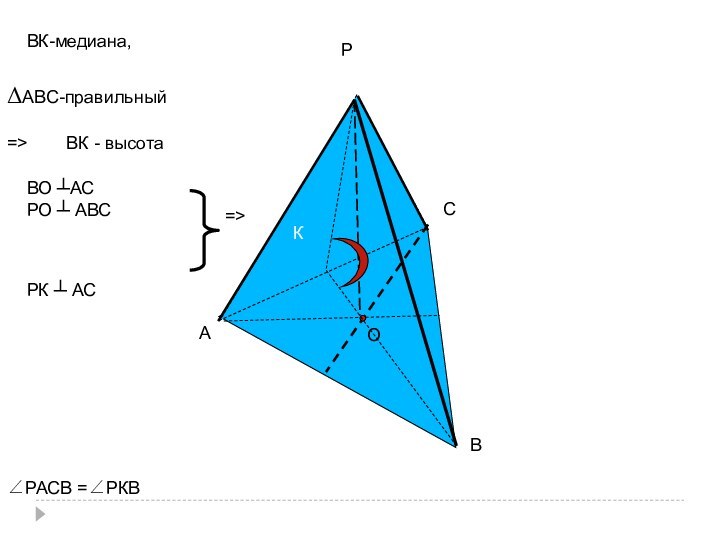
ВК - медиана,
=>
ВО ┴АС
РО ┴ АВС
=>
РК ┴ АС
ΔАВС
-правильный
ВК - высота
∠РАСВ =∠РКВ
1)
РО = √3
КО - ?
Слайд 49
С
В
К
О
А
2) ΔАВС - правильный,
О - точка пересечения
медиан,
значит:
ОВ=2ОК.
Найдем ВК.
ΔВКС:
ВК2 = ВС2-КС2;
ВК2 =
27;ВК =3√3
6
3
ВК = 3ОК,
ОК = √3
Слайд 50
Р
А
С
В
О
К
ВК - медиана,
=>
ВО ┴АС
РО ┴ АВС
=>
РК ┴ АС
ΔАВС
-правильный
ВК - высота
∠РАСВ =∠РКВ
1)
РО = √3
КО = √3
Слайд 52
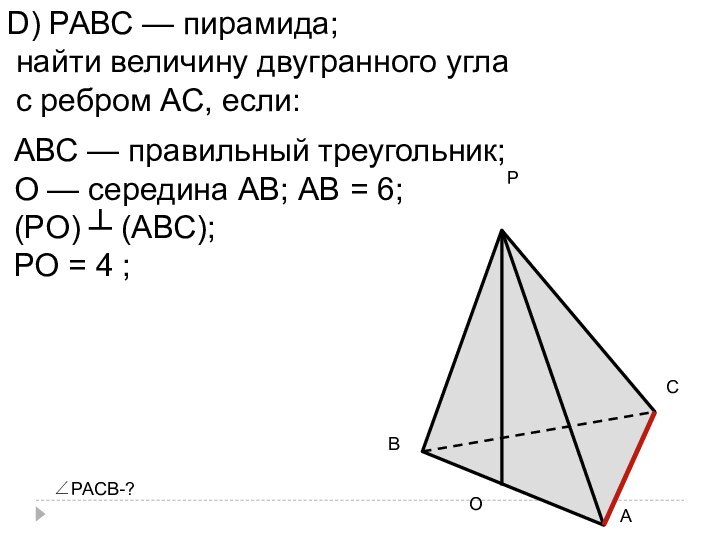
D) РАВС — пирамида;
найти величину двугранного угла
с ребром АС, если:
АВС — правильный треугольник;
О — середина
АВ; АВ = 6;(РО) ┴ (АВС);
РО = 4 ;
В
А
С
Р
О
∠РАСВ-?
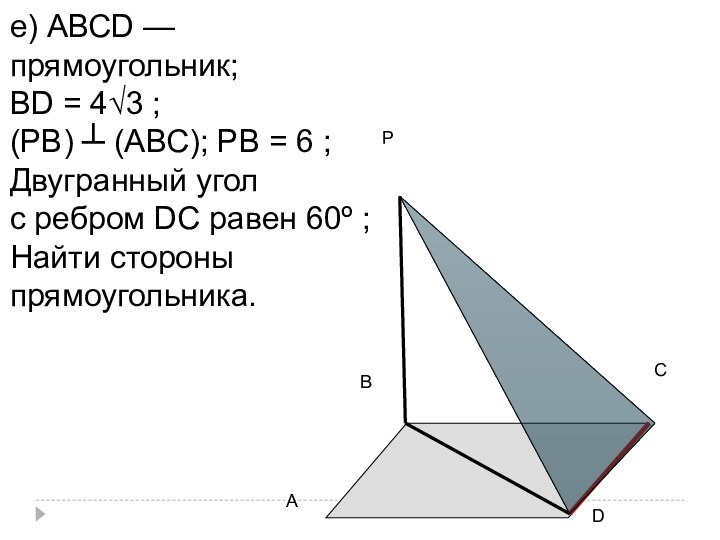
Слайд 58
е) АВСD — прямоугольник;
ВD = 4√3 ;
(РВ)
┴ (АВС); РВ = 6 ;
Двугранный угол
с ребром
DС равен 60º ;Найти стороны
прямоугольника.
В
Р
А
С
D
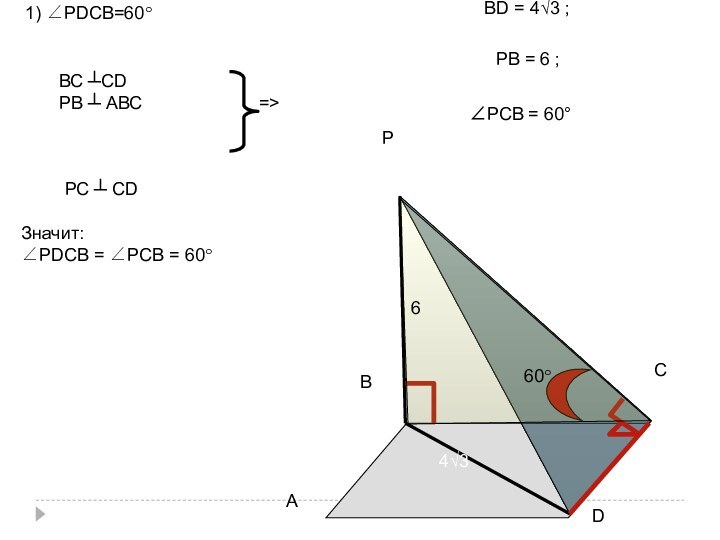
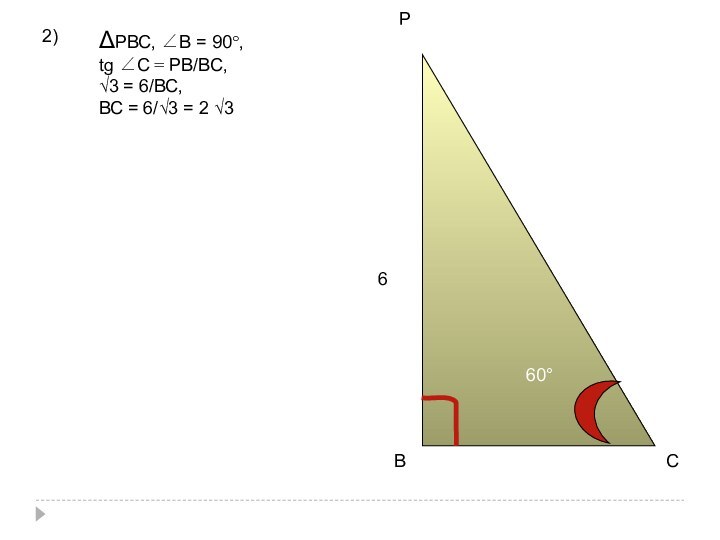
Слайд 59
В
Р
А
С
D
1) ∠РDСВ=60°
ВС ┴СD
РВ ┴ АВС
=>
РС ┴ СD
Значит:
∠РDСВ =
∠РСВ = 60°
ВD = 4√3 ;
РВ = 6 ;
∠РСВ
= 60°6
60°
4√3
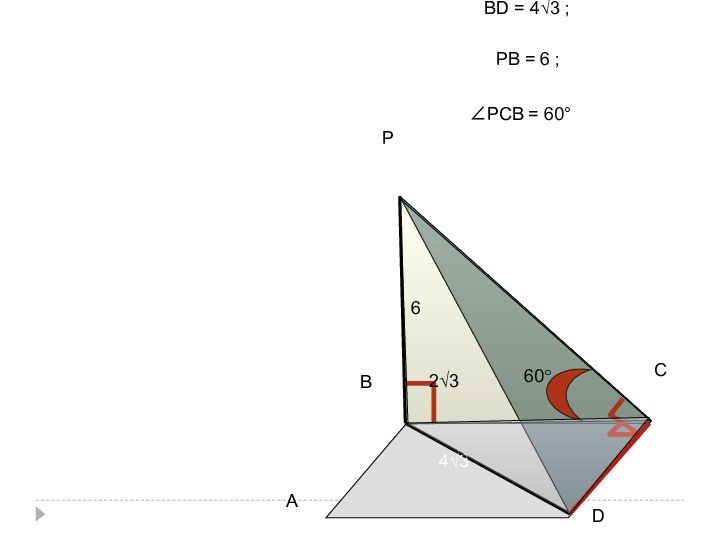
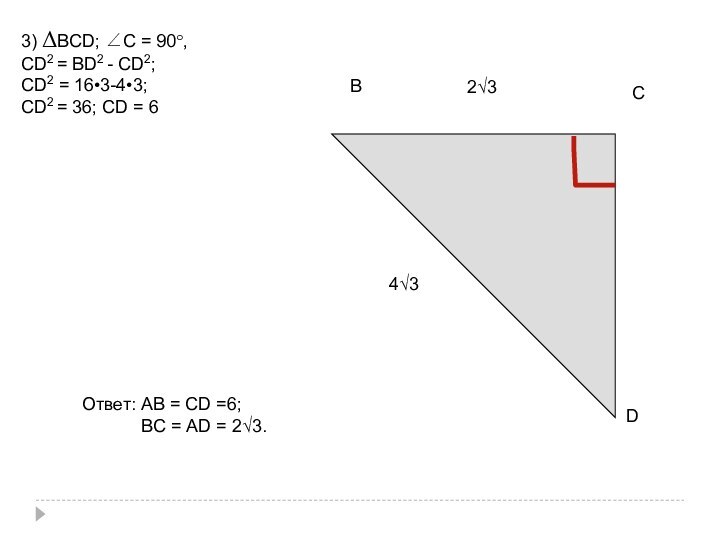
Слайд 62
В
С
D
4√3
2√3
3) ΔВСD; ∠С = 90°,
СD2 = ВD2 -
СD2;
СD2 = 16•3-4•3;
СD2 = 36; СD = 6
Ответ:
АВ = СD =6;ВС = АD = 2√3.
Слайд 63
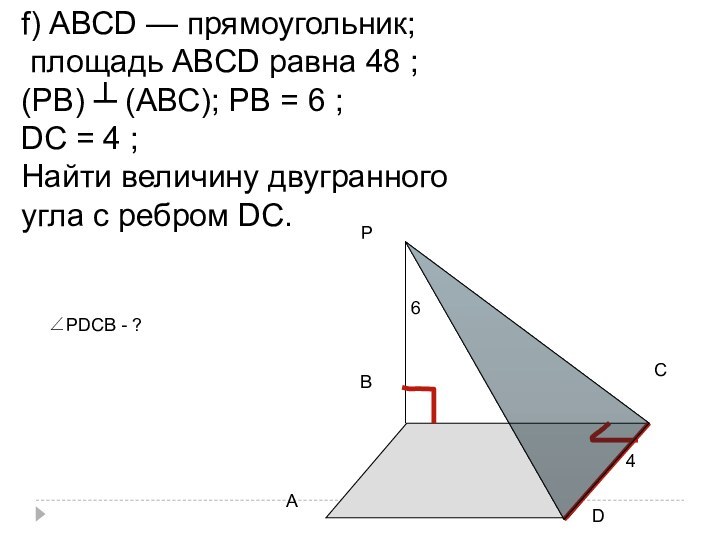
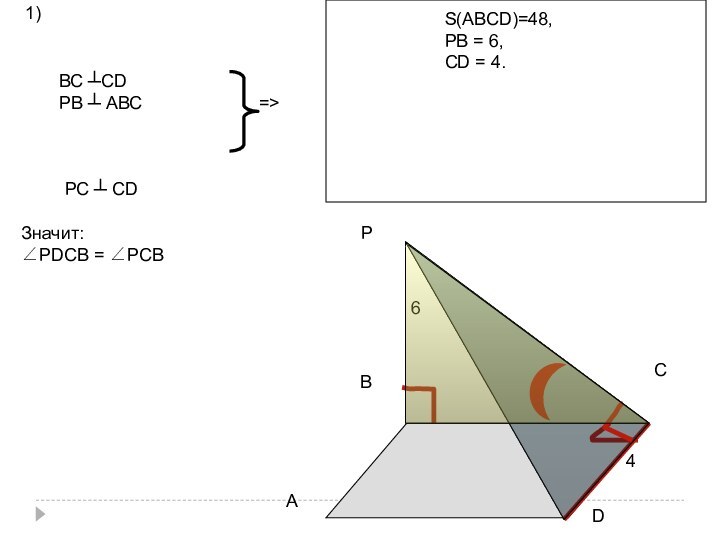
f) АВСD — прямоугольник;
площадь АВСD равна 48
;
(РВ) ┴ (АВС); РВ = 6 ;
DС = 4
;Найти величину двугранного
угла с ребром DС.
В
Р
А
С
D
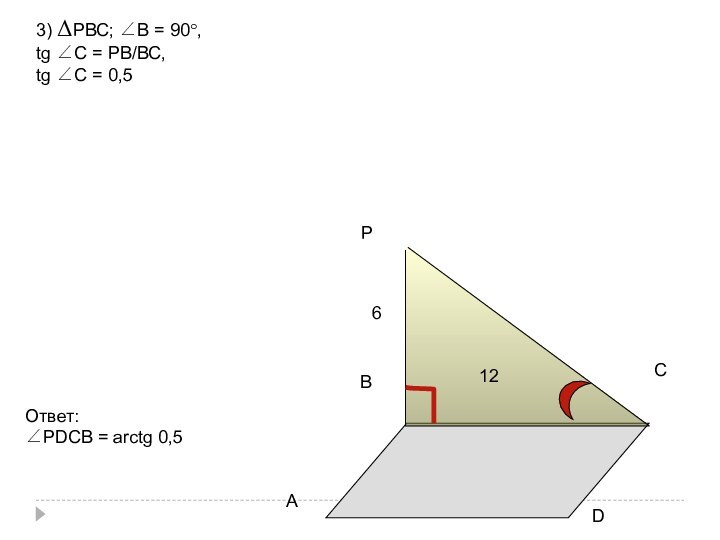
6
4
∠РDСВ - ?
Слайд 67
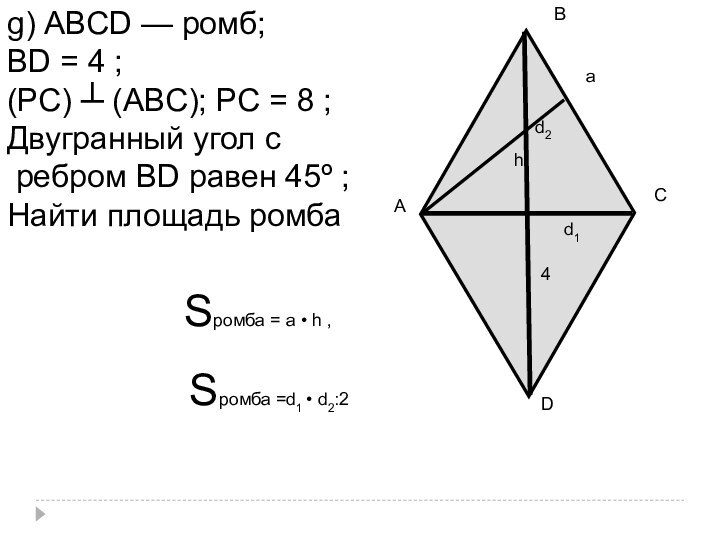
g) АВСD — ромб;
ВD = 4 ;
(РС)
┴ (АВС); РС = 8 ;
Двугранный угол с
ребром
ВD равен 45º ;Найти площадь ромба.
А
В
С
D
h
a
Sромба = a • h ,
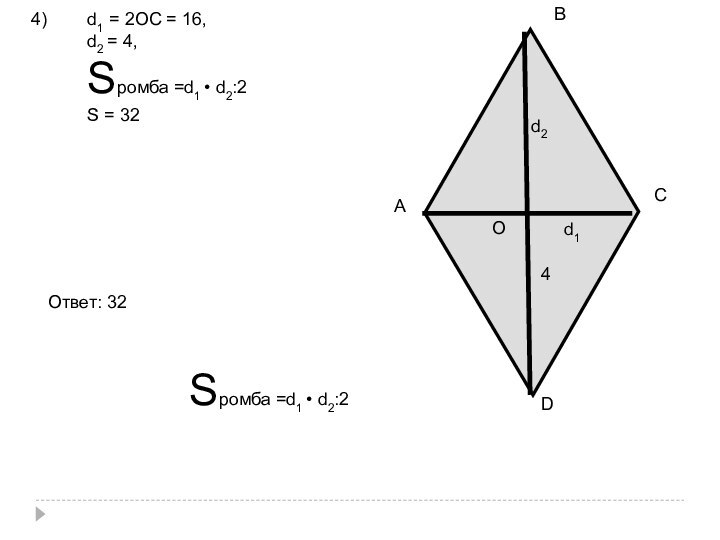
Sромба =d1 • d2:2
d1
d2
4
Слайд 68
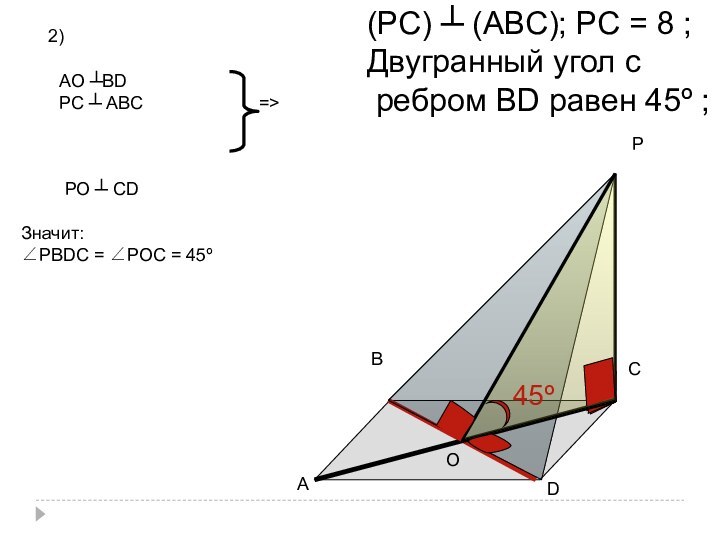
(РС) ┴ (АВС); РС = 8 ;
Двугранный угол
с
ребром ВD равен 45º ;
2)
D
А
В
С
Р
АО ┴ВD
РС ┴ АВС
=>
РО
┴ СDЗначит:
∠РВDС = ∠РОС = 45º
О
45º
Слайд 71
К) АВСD- параллелограмм;
∠АDС = 120º; АD = 8
;
DС =6 ; (РС) ┴ (АВС);
РС =
9 ; Найти величину двугранного
угла с ребром АD и
площадь АВСD .
А
В
С
D
8
120°
6
Н
Sпарал-ма= a • h
a
h
Sпарал-ма= a • b • sin∠(a,b)
b
Слайд 72
1)
А
В
С
8
120°
6
h
Sпарал-ма= a • b • sin∠(a,b)
S(АВСD) = 8
• 6 • sin 120° =24√3.
D
Н
Sпарал-ма= a • h
h
= Sпарал-ма / a h =24 √3 / 8
h =3 √3
Слайд 73
2)
A
B
C
D
P
H
(РС) ┴ (АВС); РС = 9 ;
Найти величину двугранного
угла с ребром АD
CH ┴AD
РС ┴
АВС=>
РH ┴ СD
Значит:
∠РADС = ∠РHС
9
3 √3
Слайд 74
9
3 √3
P
C
H
3) ΔРCH; ∠C = 90°,
tg ∠H =
РC/HС,
tg ∠H = 3/ √3 = √3
∠H = 60°
Ответ:
∠РADC
= 60°,S(АВСD)=24√3.
Слайд 75
Задача №2 (а)
Ребро - TM, грани: PTM, TMK;
В
грани KTM: KH┴TM, где H-середина TM (по свойству р\б
∆)В грани PTM:
в грани KMH:QL ‖ KH(по построению)
KH ┴TM(по доказанному)
=> QL┴TM (по лемме о связи ┴ и ‖);
в грани PMT: PL┴TM (по т. о 3х ┴)
ﮮ(PL;QL)=ﮮPLQ
является линейным для данного двугранного
Ответ: ﮮPLQ – линейный для двугранного PTMK
"Перпендикулярность плоскостей. Двугранный угол"
Тема №5
Дано: KMPT-тетраэдр;∆TMK правильный;Q-середина KM,Q-проекция P на TMK
Указать: линейный угол для двугранного угла PTMK
K
T
M
P
H
L
Q
Слайд 76
Задача №2 (в)
Ребро - KT, грани: PKT, KTM;
В
грани MKT: MX┴KT, где Х-середина KT (по свойству р\б
∆)QY ‖ MX (по построению)
MX┴KT (по доказанному)
=> YQ┴KT (по лемме)
В грани KTP:
PY ┴ KT (по т. о 3х ┴)
ﮮ(PY;YQ)=ﮮPYQ линейный для PKTM
Ответ: ﮮPYQ – линейный для двугранного PKTM
"Перпендикулярность плоскостей. Двугранный угол"
Тема №5
Дано: KMPT-тетраэдр;∆TMK правильный;Q-середина KM,Q-проекция P на TMK
Указать: линейный угол для двугранного угла PKTM
K
T
M
P
х
Y
Q
Слайд 77
Дополнительная задача:
COS ∟ FBCD=COS∟OKF
BF=5, BC=6
∆BFK; ∟BKF=90º FK=^25-9= =^16=4
COS∟OKF=OK/FK=
=3/4=0,75
∆OFK; ∟FOK=90º
F
C
B
A
D
K
O
Слайд 78
A
М
С
H
К
O
D
Если два плоских угла трехгранного угла равны,
то их
общее ребро проектируется на биссектрису
третьего плоского угла .
Слайд 79
Решение задач:
Боковая поверхность треугольной пирамиды равна
S, а каждое из боковых ребер l. Найдите плоские
углы при вершине, зная, что они образуют арифметическую прогрессию П/3.
Слайд 80
Проверка:
L,B,Y;
B=L+П/3; Y=B+П/3=L+2П/3
YП/3, но B=L+П/3>2П/3;
Y=L+2П/3>П/3+2П/3
Вывод:
такого угла не существует.
Слайд 81
Дополнительная задача:
Все грани параллелепипеда равные ромбы
