Слайд 2
Рассчитать простую электрическую цепь постоянного тока
Используя формулы последовательного
и параллельного соединения резисторов схема сворачивается (находится общее сопротивление
цепи)
Разворачивая в обратном порядке цепь находятся токи во всех ветвях, используя законы Ома
Слайд 3
Рассчитать сложную электрическую цепь постоянного тока методом наложения
или методом законов Кирхгофа
Метод наложения: схема разбивается на простые
(по количеству источников ЭДС). Решается каждая из простых схем. Токи в ветвях находятся как геометрическая сумма токов простых схем
Метод законов Кирхгофа. По первому закону составляется (n-1, n – количество узлов в схеме) уравнение, по второму закону – недостающие. Решается система уравнений
Проверка решения – составление баланса мощностей
Слайд 4
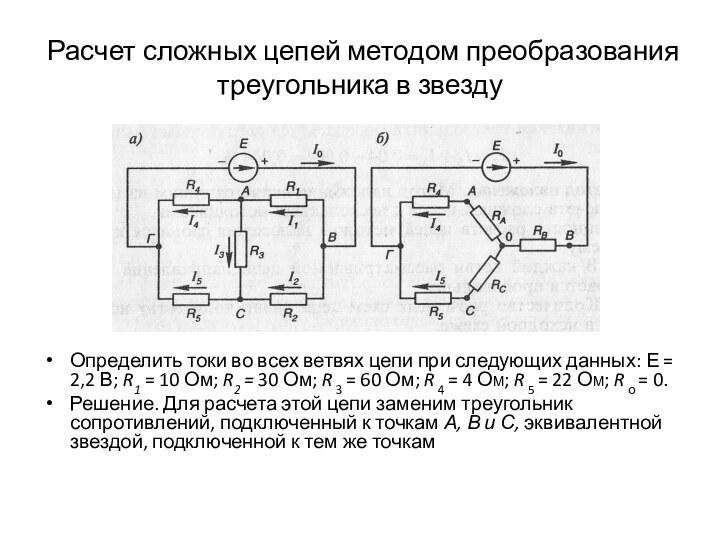
Расчет сложных цепей методом преобразования треугольника в звезду
Определить
токи во всех ветвях цепи при следующих данных: Е
= 2,2 В; R1 = 10 Ом; R2 = 30 Ом; R 3 = 60 Ом; R 4 = 4 Ом; R 5 = 22 Ом; R о = 0.
Решение. Для расчета этой цепи заменим треугольник сопротивлений, подключенный к точкам А, В и С, эквивалентной звездой, подключенной к тем же точкам
Слайд 5
Рассчитать неразветвленную цепь переменного тока
Активное сопротивление катушки Rк
= 6 Ом, индуктивное ХL = 10 Ом. Последовательно
с катушкой включено активное сопротивление R = 2 Ом и конденсатор сопротивлением Хс = 4 Ом. К цепи приложено напряжение U = 50 В (действующее значение). Определить: 1) полное сопротивление цепи: 2) ток; 3) коэффициент мощности; 4) активную, реактивную и полную мощности; 5) напряжения на каждом сопротивлении. Начертите в масштабе векторную диаграмму цепи.
Определяем полное сопротивление цепи
Определяем ток
Определяем коэффициент мощности цепи и угол: = 3650´. Угол сдвига фаз находим по синусу во избежание потери знака угла
Определяем активную мощность цепи (любая из формул)
Определяем реактивную мощность цепи (любая из формул)
Определяем полную мощность цепи (любая из формул)
Слайд 6
Рассчитать неразветвленную цепь переменного тока
7. Определяем падения напряжения
на сопротивлениях цепи
8. Построение векторной диаграммы начинаем с выбора
масштаба для тока и напряжения. Задаемся масштабом по току: в 1 см — 1,0 А и масштабом по напряжению: в 1 см — 10 В. Построение векторной диаграммы начинаем с вектора тока, который откладываем по горизонтали в масштабе.
Вдоль вектора тока откладываем векторы падений напряжения на активных сопротивлениях
Из конца вектора UR откладываем в сторону опережения вектора тока на 90º вектор падения напряжения UL на индуктивном сопротивлении
Из конца вектора UL откладываем в сторону отставания от вектора тока на 90° вектор падения напряжения на конденсаторе UС
Геометрическая сумма векторов равна полному напряжению U, приложенному к цепи
Слайд 7
Рассчитать разветвленную цепь переменного тока
Катушка с активным сопротивлением
R = 6 Ом и индуктивным ХL1 = 8
Ом соединена параллельно с конденсатором, емкостное сопротивление которого ХС = 10 Ом. Определить: 1) токи в ветвях и в неразветвленной части цепи; 2) активные к реактивные мощности ветвей и всей цепи; 3) полную мощность цепи; 4) углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи. Начертить в масштабе векторную диаграмму цепи. К цепи приложено напряжение U = 100 В
Определяем токи в ветвях
Углы сдвига фаз в ветвях находим по синусам углов во избежание потери знака угла
Определяем косинусы угла
Определяем активные и реактивные составляющие токов в ветвях
Определяем ток в неразветвленной части цепи
Слайд 8
Рассчитать разветвленную цепь переменного тока
6. Определяем коэффициент мощности
всей цепи
7. Определяем активные и реактивные мощности ветвей и
всей цепи
8. Определяем полную мощность цепи
9. Для построения векторной диаграммы задаемся масштабом со току: в 1 см — 2,5 А и масштабом по напряжению: в 1 см — 25 В. Построение начинаем с вектора напряжения U. Под углом 1 к нему (в сторону отставания) откладываем в масштабе вектор тока I1, под углом 2 (в сторону опережения) — вектор тока I2. Геометрическая сумма этих токов равна току в неразветвленной части цепи. На диаграмме показаны также проекции векторов токов на вектор напряжения (активная составляющая Iа1) и вектор, перпендикулярный ему (реактивные составляющие Iр1и Iр2).
Слайд 9
Рассчитать трехфазную цепь, соединенную звездой
В трехфазную четырехпроводную сеть

включили звездой несимметричную нагрузку: в фазу А — конденсатор
с емкостным сопротивлением ХА = 10 Ом; в фазу В — активное сопротивление RВ = 0 Ом и индуктивное ХВ = 6 Ом, в фазу С — активное сопротивление RС = 5 Ом. Линейное напряжение сети UН = 380 В. Определить фазные токи, начертить в масштабе векторную диаграмму цепи и найти графически ток в нулевом проводе
Определяем фазные напряжения установки
Находим фазные токи
Для построения векторной диаграммы выбираем масштабы по току: 1 см — 10 А и по напряжению: 1 см — 100 В. Построение диаграммы начинаем с векторов фазных напряжений UА, UВ, UС, располагая их под углом 120º друг относительно друга. Ток IА опережает напряжение UА на угол 90 º; ток IВ отстает от напряжения UВ на угол В, который определяется из выражения: . Ток IС совпадает с напряжением UС. Ток в нулевом проводе равен геометрической сумме трех фазных токов. Измеряя длину вектора тока I0, которая сказалась равной 6,8 см. находим ток I0 = 68 А
Слайд 10
Рассчитать трехфазную цепь, соединенную треугольником
В трехфазную сеть включили

треугольником несимметричную нагрузку : в фазу AВ — конденсатор
с емкостным сопротивлением ХАВ = 10 Ом; в фазу ВС— катушку с активным сопротивлением RВС = 4 Ом и индуктивным ХВС = 3 Ом; в фазу СА — активное сопротивление RСА = 10 Ом. Линейное напряжение сети UН = 220 В. Определить фазные токи, углы сдвига фаз и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовые значения линейных токов.
Определяем фазные токи и углы сдвига фаз
Для построения векторной диаграммы выбираем масштабы по току: 1 см — 10 А и по напряжению: 1 см — 80 В. Затем в принятом масштабе откладываем векторы фазных (они же линейные) напряжений UАВ, UВС, UСА под углом 120º друг относительно друга. Под углом АВ = —90° к вектору напряжения UАВ откладываем вектор тока IАВ; в фазе ВС вектор тока IВС должен отставать от вектора напряжения UВС на угол ВС = 36°50´, а в фазе СА вектор тока IСА совладает с вектором напряжения UСА. Затем строим векторы линейных токов на основании известных уравнений
Измеряя длины векторов линейных токов и пользуясь принятым масштабом, находим значения линейных токов: IА = 11А, IВ = 57А, IС = 47А
Слайд 11
Рассчитать добавочные сопротивления к многопредельному вольтметру
Предел измерения
вольтметра электромагнитной системы составляет 7,5 В при внутреннем сопротивлении
Rв = 200 Ом. Определить добавочное сопротивление, которое необходимо включить для расширения предела измерения до 600 В.
Решение:
Слайд 12
Рассчитать емкость или индуктивность с помощью авометра и
источников постоянного и переменного токов
Для расчета емкости необходим источник
питания переменного тока с известной частотой (измеряются напряжение, ток)
Для расчета индуктивности необходимы оба источника (измеряются напряжение, ток). Если источник постоянного тока – определяем активное сопротивление катушки, если источник переменного тока – полное сопротивление катушки