- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему И. ЛакатосДоказательства и опровержения
Содержание
- 2. Формула ЭйлераV-E+F = 2для V вершин, Е ребер, F граней многогранника
- 3. Доказательство теоремыПервый шаг. Вообразим, что многогранник будет
- 4. Примеры и контрпримерыДля каждого куба V —
- 5. Примеры и контрпримерыЭта картинная рама совсем не
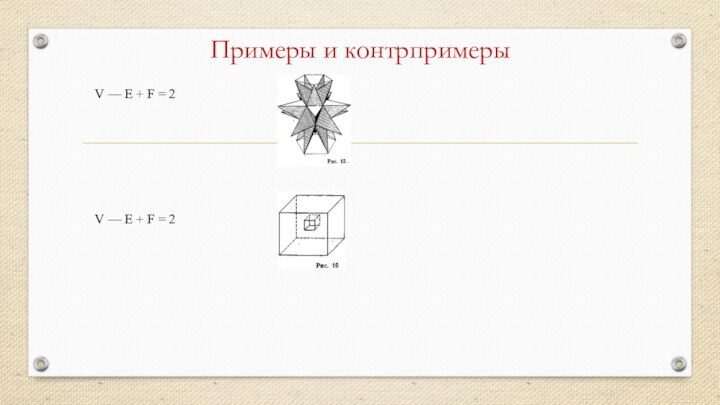
- 6. Примеры и контрпримерыV — Е + F = 2V — Е + F = 2
- 7. «Квазигенетическое доказательство»Для многоугольников V = Е. Теперь
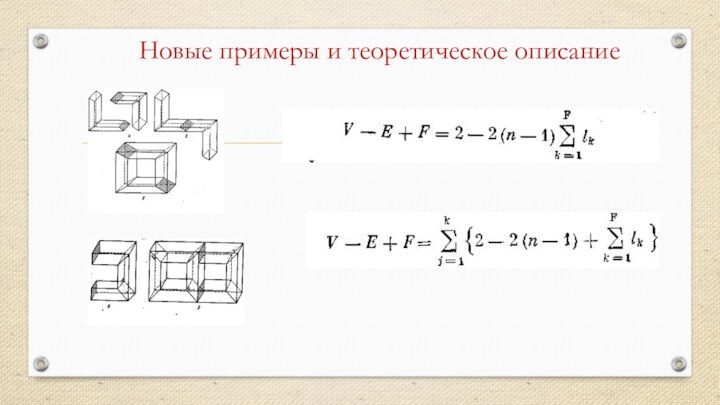
- 8. Новые примеры и теоретическое описание
- 9. Скачать презентацию
- 10. Похожие презентации







Слайд 3
Доказательство теоремы
Первый шаг. Вообразим, что многогранник будет полым
с поверхностью из резины. Если мы вырежем одну из
его граней, то всю остальную поверхность мы можем, не разрезая, растянуть на плоской доске. Грани и ребра будут деформироваться, ребра могут стать криволинейными, но V, Е и F не изменятся, так что если и только если V — Е + F = 2 для первоначального многогранника, то V — Е + F — 1 для этой плоской сети — вспомните, что мы одну грань удалили. (На рис. 1 показана такая сеть для куба.)Второй шаг. Теперь мы стриангулируем нашу карту — она действительно выглядит как географическая карта. Проведем (может быть, криволинейные) диагонали в тех (может быть, криволинейных) многоугольниках, которые еще не являются (может быть, криволинейными) треугольниками. Проведя каждую диагональ, мы увеличиваем и E и F на единицу, так что сумма V — Е + F не изменится (рис. 2).
Третий шаг. Теперь будем вынимать из триангулированной сети треугольники один за другим. Вынимая треугольник, мы или вынимаем ребро, причем исчезают одна грань и одно ребро (рис. 3, а), или вынимаем два ребра и вершину; тогда исчезают одна грань, два ребра и одна вершина (рис. 3, б). Таким образом, если V — Е + F = 1 до выемки треугольника, то оно останется таким же и после выемки. В конце этой процедуры мы получаем один треугольник. Для него V — Е + F = 1 является справедливым. Таким образом, мы доказали нашу догадку.
Слайд 4
Примеры и контрпримеры
Для каждого куба V — Е
+ F = 2,
так что для полого куба
F — Е + F = 4В обоих случаях V — Е + F = 3
V — Е + F = —6
Определение 1. Многогранником называется тело, поверхность которого состоит из многоугольников — граней.
Определение 2. Многогранник есть поверхность, состоящая из системы многоугольников.
Определение 3. Под многогранником подразумевается система многоугольников, расположенных таким образом, чтобы (1) на каждом ребре встречались только два многоугольника и (2) чтобы было возможно изнутри одного многоугольника пройти во внутрь другого любой дорогой, которая никогда не пересекает ребра в вершине.
Определение 4. Многоугольником называется система ребер, расположенных таким образом, что (1) в каждой вершине встречаются только два ребра и (2) ребра не имеют общих точек, кроме вершин.
Определение 4‘. Многоугольником называется система ребер, расположенных таким образом, что (1) в каждой вершине встречаются только два ребра.
Слайд 5
Примеры и контрпримеры
Эта картинная рама совсем не настоящий
многогранник. Возьмите какую-нибудь точку в «туннеле» — пространстве, ограниченном
рамой. Проведите плоскость через эту точку. Вы найдете, что всякая такая плоскость будет всегда с картинной рамой иметь два поперечных сечения, составляющих два отдельных, совершенно не связанных многоугольника! (рис. 10).Определение 5. В случае настоящего многогранника через любую точку пространства можно провести по крайней мере одну плоскость, сечение которой с многогранником будет состоять из одного лишь многоугольника.
V — Е + F = 0
16—24 + 11 = 3
Слайд 7
«Квазигенетическое доказательство»
Для многоугольников V = Е. Теперь многоугольник
есть система многоугольников, состоящая из одного единственного многоугольника. Многогранник
есть система многоугольников, состоящих более чем из одного многоугольника. Но для многогранников VE. В каком пункте отношение V=E отказалось служить при переходе от монополигональных систем к полиполигональным?Закрытие может быть произведено, если мы такую сосудообразную систему покроем многоугольником — крышкой; прикрепление такого покрывающего многоугольника увеличит F на единицу без изменения V или Е
Для всякого многоугольника Е—V = 0 (рис. 17, а). Что случится, если я прикреплю к нему другой многоугольник (необязательно в той же плоскости)? Добавляемый многоугольник имеет n1 сторон и n1 вершин; если мы прикрепим его к первоначальному по цепочке из n1' ребер и n1'+1 вершин, то мы увеличим число ребер на n1— n1', а число вершин на n1— (n1' + 1); значит, в новой 2-полигональной системе получится избыток в числе ребер над числом вершин: Е — V = 1 (рис. 17,6); необычное, но совершенно допустимое прикрепление мы видим на рис. 17, в. «Прикрепление» новой грани к системе будет всегда увеличивать этот избыток на единицу; следовательно, для построенной таким образом F-полигональной системы будет всегда E—V=F—1.
Для закрытой полигональной системы — и закрытого многогранника,— построенной таким образом, V—E+F=2
Для треугольника V—E=0.
Для одного ребра V — Е = 1 (рис. 18,а).
Присоединение новых ребер всегда увеличивает на единицу и число ребер и число вершин (рис. 18,6 и 18,в).
Почему же тогда в полигональных системах ребер будет V — Е = 0? Это получается вследствие перехода от открытой системы ребер (которая ограничивается двумя вершинами) к закрытой системе ребер (которая не имеет такой границы), так как мы «закрываем» открытую систему, вставляя ребро без добавления новой вершины. Таким образом, доказывается, но не наблюдается, что для многоугольников будет V—Е = 0.
Для одной вершины V = 1 (рис. 19).