Презентация на тему Исследование фракталов в искусстве

«В математике есть своя красота,

как в живописи и поэзии»
Н. Е. Жуковский

удивили меня, поэтому захотелось вызвать интерес у общественности к

данной теме.












Результаты показывают, что очень малое количество учащихся ( 12% ), знают, что такое «фрактал».

12%

20%

68%

компьютерных программ и использовать их при построении фракталов.
3.Вызвать интерес

у одноклассников, дать стимул к изучению и дальнейшему исследованию фракталов.
Задачи:
1.Познакомиться с понятием фрактала, выявить его геометрический смысл.
2.Доказать универсальность в применении и распространении фракталов в жизни человека.
3.Исследовать фрактальность в искусстве на примере картин известных художников прошлого и работ современных художников.
4.Построить графическую и компьютерную модель фрактала.
5.Создать небольшую выставку работ.

увеличенные части похожи на сами объекты и друг на

друга. При этом как форма и размер отдельных элементов, так и их взаимное расположение может быть описано с помощью математической формулы.

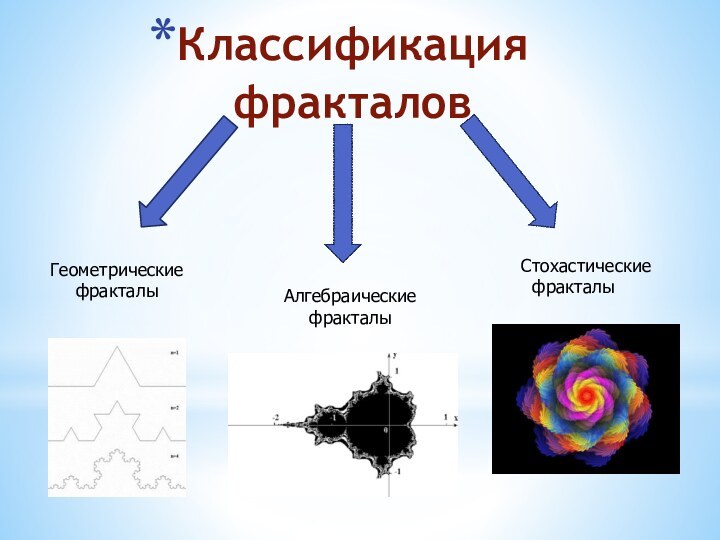
Треугольник Серпинского

Луи Фату описал это множество в начале 19 века,

но так как в то время не было вычислительной техники, его теории не получили развития

Само слово «фрактал» появилось благодаря гениальному ученому Бенуа Мандельброту в конце 19 века.

Гастона Мориса Жюлиа.

Лорен Карпентер в 1978 году серьезно изучил

принципы фрактальной геометрии и на своем компьютере с помощью формул нарисовал вполне узнаваемый горный пейзаж.

ван Гойен
Кэрри Митчелла
Вячеслав Усеинов

и способы создания и обработки изображений на экране компьютера

с помощью специальных программ

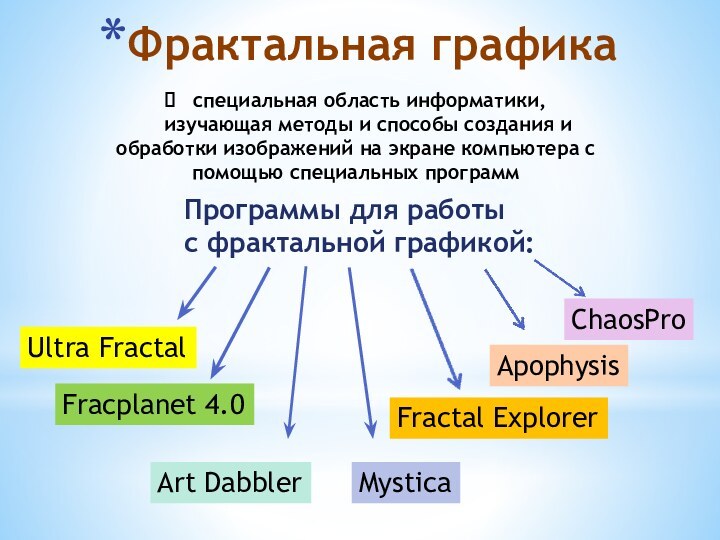
Программы для работы
с фрактальной графикой:

Fracplanet 4.0

Ultra Fractal

ChaosPro

Fractal Explorer

Mystica

Apophysis

Art Dabbler

создания красочных принтов, в дальнейшем используя их для оформления

элементов одежды. Так же можно создавать красивые узоры и использовать их в оформлении школьных канцелярских товаров, элементов декора, цветочных панно или элементов ландшафта, кроме того можно применять их для создания красочных обоев, постельного белья, оформлении мебели или же в виде необычных рисунков на дверях и паркете. Используя фрактальные рисунки в оформлении визитки, афиши или рекламного баннера, вы будете обеспечены потоком клиентов и посетителей, так как яркий и запоминающийся фрактал обязательно привлечёт к себе внимание.