Слайд 2
Класс точности средства измерений – это его характеристика,
отражающая точностные возможности средств измерений данного типа.
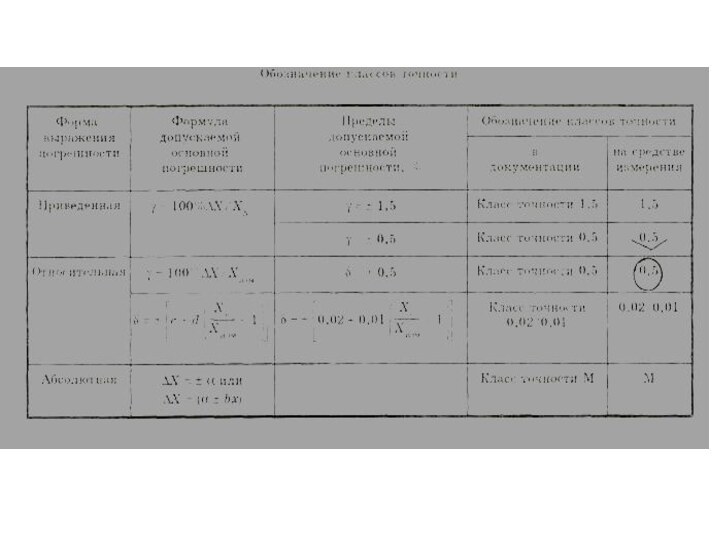
Допускается буквенное или
числовое обозначение классов точности. Средствам измерений, предназначенным для измерения двух и более физических величин, допускается присваивать различные классы точности для каждой измеряемой величины. Средствам измерений с двумя или более переключаемыми диапазонами измерений также допускается присваивать два или более класса точности.
Если нормируется предел допускаемой абсолютной основной погрешности, или в различных поддиапазонах измерений установлены разные значения пределов допускаемой относительной основной погрешности, то, как правило, применяется буквенное обозначение классов.
Слайд 3
Существует несколько способов задания классов точности приборов.
Первый способ
используется для мер. При этом способе указывается порядковый номер
класса точности меры. Например, нормальный элемент 1 класса точности, набор гирь 2 класса точности.
Порядок вычисления погрешностей в этом случае определяют по технической документации, прилагаемой к мере.
Слайд 4
Второй способ предусматривает задание класса точности для приборов
с преобладающими аддитивными погрешностями (это большинство аналоговых приборов). В
этом случае класс точности задается в виде числа К (без кружочка), например 1,5; 2,0; 4,0. При этом нормируется основная приведенная погрешность γ Х прибора, выраженная в процентах, которая во всех точках шкалы не должна превышать по модулю числа К, то есть |γХ| < К, %.
Число К выбирается из ряда значений (1,0; 1,5; 2; 2,5; 4,0; 5,0; 6,0)*10n, где п= 1, 0, -1,-2.
Слайд 5
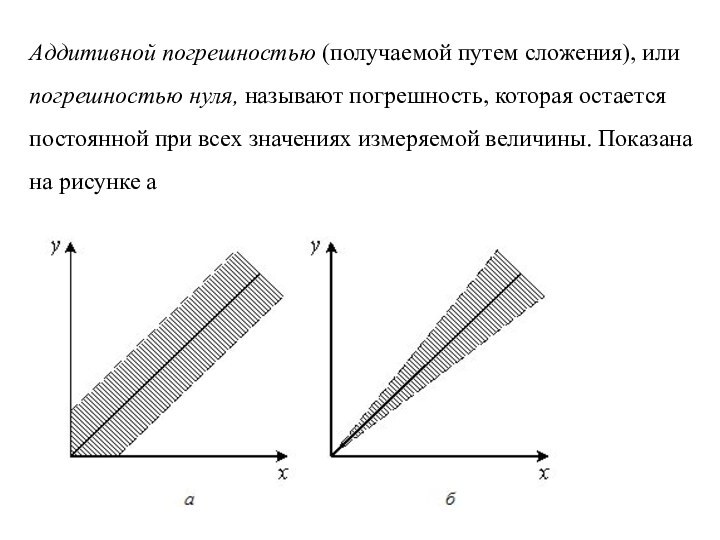
Аддитивной погрешностью (получаемой путем сложения), или погрешностью нуля,
называют погрешность, которая остается постоянной при всех значениях измеряемой
величины. Показана на рисунке а
Слайд 6
Третий способ предусматривает задание класса точности для приборов
с преобладающими мультипликативными погрешностями. В этом случае нормируется основная
относительная погрешность, выраженная в процентах, так, что | δX | < К,%. Класс точности задается в виде числа К в кружочке, например
Число К выбирается из приведенного выше ряда.
Слайд 7
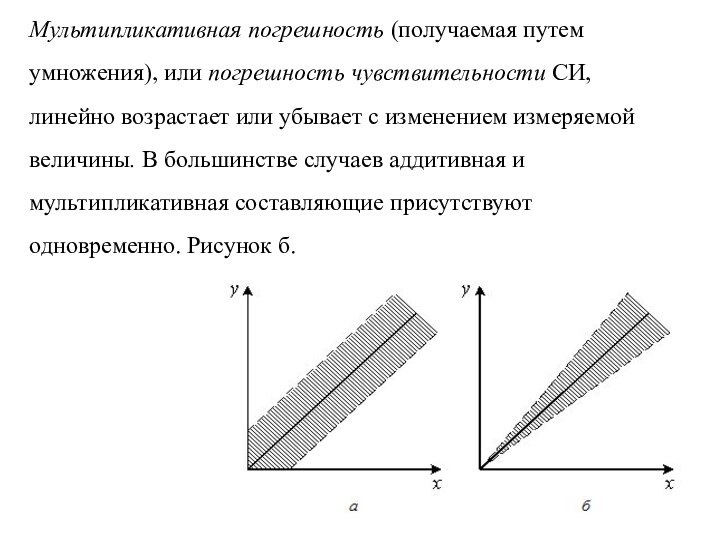
Мультипликативная погрешность (получаемая путем умножения), или погрешность чувствительности
СИ, линейно возрастает или убывает с изменением измеряемой величины.
В большинстве случаев аддитивная и мультипликативная составляющие присутствуют одновременно. Рисунок б.
Слайд 8
Четвертый способ предусматривает задание класса точности для приборов
с соизмеримыми аддитивными и мультипликативными погрешностями.
Аддитивные погрешности не зависят
от измеряемой величины X , а мультипликативные прямо пропорциональны значению X.
Источники аддитивной погрешности - трение в опорах, неточность отсчета, шум, наводки и вибрации. От этой погрешности зависит наименьшее значение величины, которое может быть измерено прибором..
Слайд 9
Причина мультипликативных погрешностей: влияние внешних факторов и старение
элементов и узлов приборов.
В этом случае класс точности задается
двумя числами а/b, разделенными косой чертой, причем а>b. При этом нормируется основная относительная погрешность, выраженная по формуле:
δХ < [ а + b ( Хк /Х - 1)] , %.
где Хк - максимальное конечное значение пределов измерения. Число а отвечает за мультипликативную составляющую погрешности, а число b за аддитивную. Значения а и b выбираются из вышеприведенного ряда.
К приборам, класс точности которых выражается дробью, относятся цифровые приборы, а также мосты и компенсаторы