Слайд 2
Абстрактный тип данных
Функция:
Обобщение понятия оператора.
Инкапсулирование частей алгоритма.
Абстрактный тип
данных – математическая модель с совокупностью операторов, определённых в
рамках этой модели.
Обобщение простых типов данных.
Инкапсулирование операторов, определённых для АТД.
Слайд 3
АТД
Тип данных – множество значений, которые может принимать
переменная данного типа.
Структуры данных для представления АТД – набор
переменных различных типов, объединённых определённым образом.
Базовый строительный блок структуры данных – ячейка, предназначенная для хранения значения определенного базового или составного типа данных.
Слайд 5
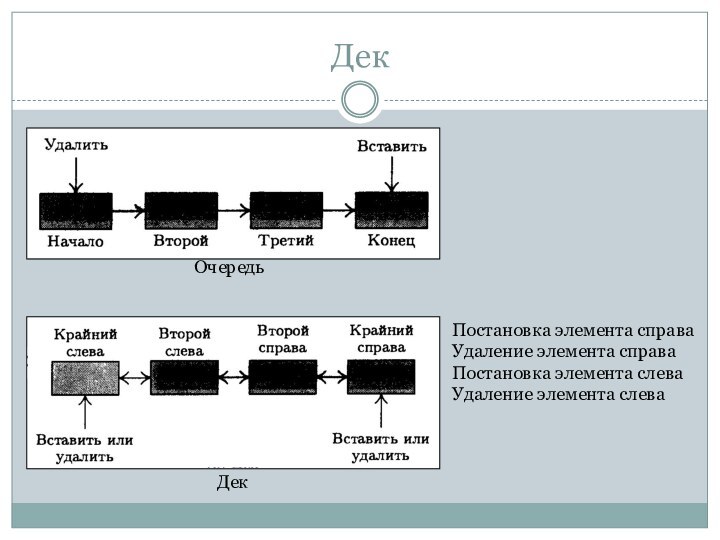
Линейный список
Линейные списки, у которых операции вставки, удаления
и доступа к данным выполняются в первом или последнем
узле:
Стек – линейный список, в котором все операции вставки и удаления выполняются на одном из концов списка;
Очередь (односторонняя очередь) – линейный список, в котором все операции вставки выполняются на одном из концов списка, а все операции удаления – на другом;
Дек (двусторонняя очередь) – линейный список, в котором все операции вставки и удаления выполняются на обоих концах списка.
Слайд 7
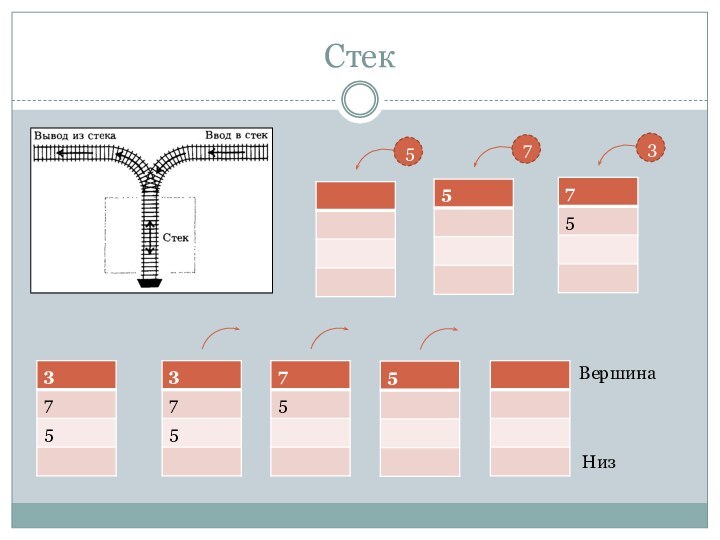
Стек
Принцип обслуживания в обратном порядке LIFO: Last-in-First-out. Первым
удаляется тот элемент, который был помещён в стек последним.
Добавление
в стек: объект кладётся на стек (операция проталкивания - push).
Удаление из стека: снимается верхний элемент стека (операция выталкивания - pop).
Слайд 8
Реализация стека
Если stack – стек размера SIZE:
push(stack, n)
– положить (протолкнуть) n на стек stack;
pop(stack) – снять
(вытолкнуть) верхний элемент со стека stack;
Стек может быть сымитирован при помощи массива stack и указателя стека sp (stack pointer). Если стек пуст, то sp = -1.
Слайд 9
Реализация стека
sp
-1
sp
-1
push(stack, 2)
sp
-1
push(stack, 5)
sp
-1
push(stack, -3)
sp
-1
push(stack, 10)
sp
-1
pop(stack)
sp
-1
pop(stack)
sp
-1
push(stack, 4)
Слайд 10
Реализация стека
Если предпринимается попытка снять элемент с пустого
стека (sp==-1), говорят, что возникает недостаток элементов (underflow) -
стек опустошается. Недостаток элементов, как правило не является ошибкой.
Если элемент кладётся на заполненный стек (sp==SIZE), говорят, что возникает избыток элементов (overflow) – стек переполняется . Как правило, это считается ошибкой, так как положить элемент на стек необходимо, но места в стеке для него нет.
Проверка как на опустошение, так и на переполнение должны обрабатываться при программной реализации стека.
Слайд 11
Реализация стека
push(stack, m)
Если (стек_не_заполнен) {
sp++; // модификация указателя
stack[sp] = m; // сохранение
} иначе {
// переполнение
}
Слайд 12
Реализация стека
pop(stack)
Если (стек_не_пуст) {
снять stack[sp]; // выталкивание
sp--;
// модификация указателя
} иначе {
// опустошение;
}
Слайд 13
Очередь
Принцип обслуживания в порядке поступления FIFO: First-in-First-out. Первым
удаляется тот элемент, который был помещён в очередь первым.
Очередь
имеет начало – front и конец – rear.
Добавление в очередь: со стороны конца объект ставится в очередь (операция помещения в очередь - enqueue).
Удаление из очереди: со стороны начала объект выводится из очереди (операция вывода из очереди - dequeue).
Слайд 14
Реализация очереди
Если queue – очередь размера SIZE:
enqueue(queue, n)
– поместить n в очередь queue;
dequeue(queue) – вывести первый
элемент из очереди queue;
Очередь может быть сымитирована при помощи массива queue и указателя front на начало очереди и rear на конец очереди.
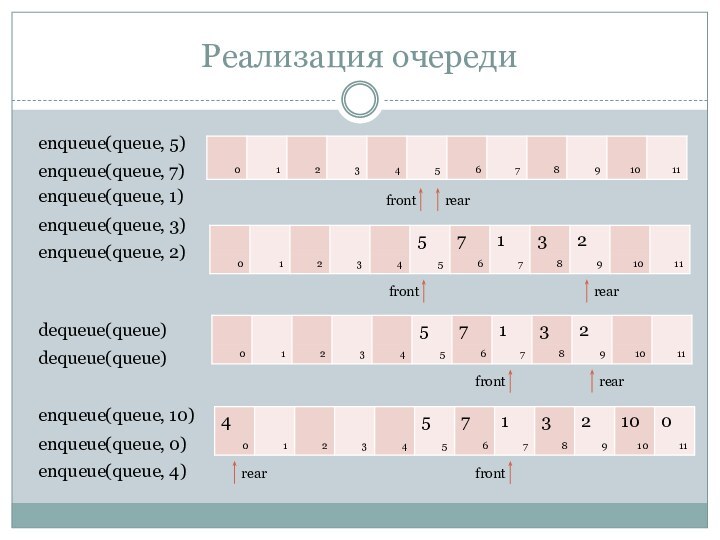
Слайд 15
Реализация очереди
front
rear
rear
rear
rear
enqueue(queue, 5)
enqueue(queue, 7)
enqueue(queue, 1)
enqueue(queue, 3)
enqueue(queue, 2)
front
front
front
dequeue(queue)
dequeue(queue)
enqueue(queue, 10)
enqueue(queue,
0)
enqueue(queue, 4)
Слайд 16
Реализация очереди
Для удобства стоит положить front=rear=0.
При работе с
очередью может возникнуть недостаток элементов (underflow) и избыток элементов
(overflow).
В случае, если реализована циклическая организация очереди (по достижении последней ячейки массива запись происходит в первую):
очередь можно считать полной, если после добавления нового элемента rear совпадает с front;
очередь можно считать пустой, если перед удалением элемента выясняется, что rear совпадает с front.
Слайд 17
Реализация очереди
enqueue(queue, m)
Если (rear == SIZE)
{ // закольцевать
rear = 0;
} иначе {
rear++;
}
Если (rear == front) { // избыток
// переполнение
} иначе {
queue[rear] = m;
}
rear
front
rear
front
Слайд 18
Реализация очереди
dequeue(queue)
Если (rear == front) {
// недостаток
// опустошение
}
иначе {
Если (front == SIZE) {
front = 0;
} иначе {
front++;
}
вывести queue(front);
}
rear
front
rear
front
Слайд 19
Очередь с приоритетами
Очередь с приоритетами priorityQueue– АТД на
модели множеств с операторами добавления в очередь и удаления
из очереди элемента с минимальным приоритетом: enqueue и dequeueMin.
enqueue понимается в обычном смысле, dequeueMin является функцией, которая возвращает элемент с наименьшим приоритетом и удаляет его из очереди.
При организации АТД priorityQueue следует учесть, что ячейка данного линейного списка содержит не только значение, но и его приоритет. Таким образом функция постановки в очередь принимает следующий вид:
enqueue(priorityQueue, key, priority)
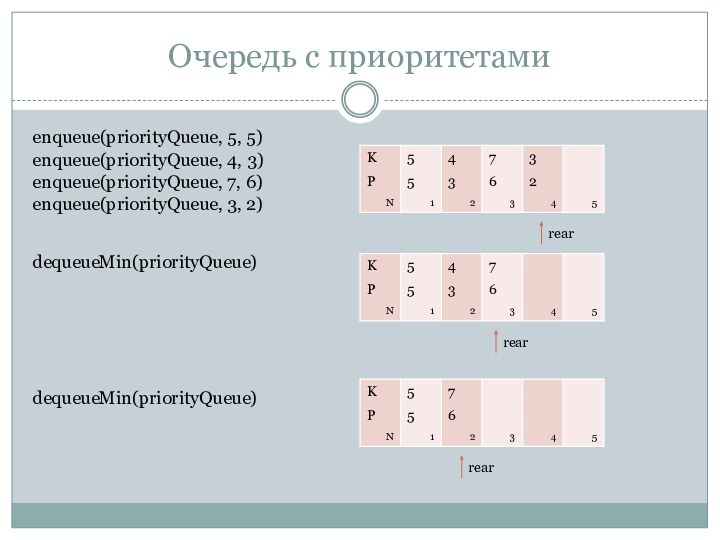
Слайд 20
Очередь с приоритетами
enqueue(priorityQueue, 5, 5)
enqueue(priorityQueue, 4, 3)
enqueue(priorityQueue, 7,
6)
enqueue(priorityQueue, 3, 2)
rear
dequeueMin(priorityQueue)
rear
dequeueMin(priorityQueue)
rear










![Лекция 3.Линейные структуры данных Реализация стекаpop(stack) Если (стек_не_пуст) { снять stack[sp]; //](/img/tmb/14/1370462/bbb92ba98d8e3a417f72a11ec568a38c-720x.jpg)