- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Нечеткая логика
Содержание
- 3. С = {0,04/молоко; 0,15/творог; 0,25/сливки; 0,35/ сыр; 0,40/сметана; 0,78/масло; 0,98/топленое масло} µс(х).
- 5. Примеры записи нечеткого множества Пусть E =
- 7. Рассмотрим нечеткое множество A , соответствующее понятию
- 10. Примеры нечетких множеств 1. Пусть E =
- 11. Нечеткая переменная характеризуется тройкой , гдеα -
- 12. Лингвистической переменной называется набор , гдеβ -
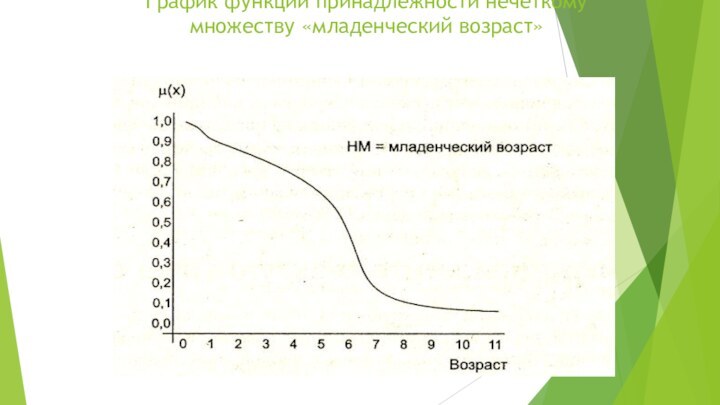
- 15. График функции принадлежности нечеткому множеству «младенческий возраст»
- 16. Пример: Пусть эксперт определяет толщину выпускаемого изделия
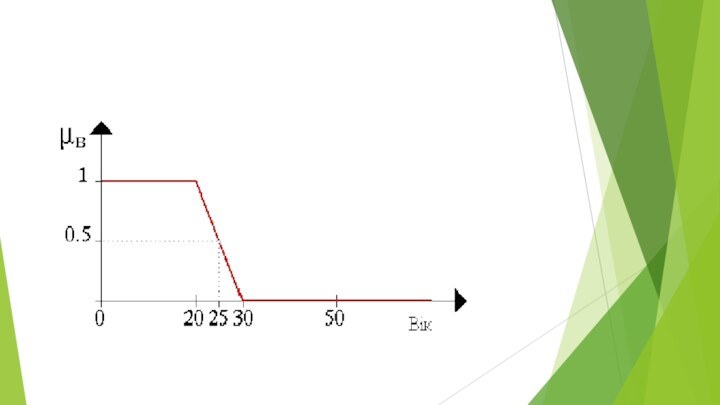
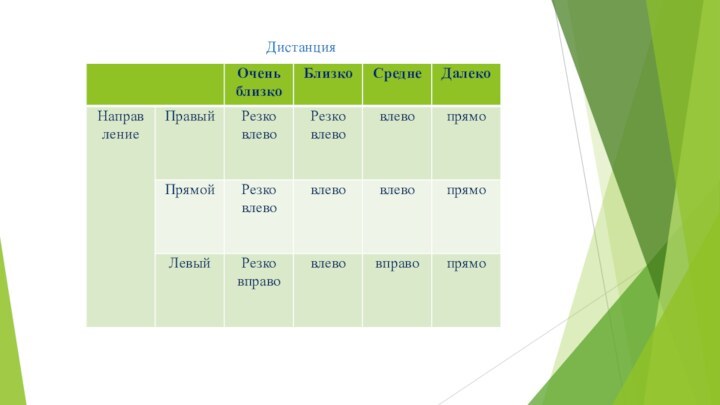
- 17. Дистанция
- 18. Преимущества нечетких систем возможность оперировать нечеткими входными
- 19. Применение нечетких систем CubiCalc 2.0 RTC -
- 20. Использование нечеткого управления рекомендуется... для очень сложных
- 22. Фотоаппараты и видеокамеры используют нечеткую логику, чтобы
- 23. Японский город Сендай имеет метрополитен с 16
- 24. Автоматическое управление воротами плотины на гидроэлектростанциях
- 25. Улучшение эффективности и оптимизация промышленных систем управления
- 26. Распознавание движения изображения в видеокамерах (Canon,
- 27. САПР производственных процессов (Aptronix, Harima, Ishikawajima-OC
- 28. Основные характеристики нечетких множеств
- 29. Пусть M = [0,1] и A -
- 30. μС(х)=max{μA(х), μB(х)}, х1. Объединением нечетких множеств A
- 32. Нечеткое множество «между 5 и 8 ИЛИ (OR) около 4» показано здесь
- 33. 4. ПересечениеПересечением нечетких множеств А и В
- 35. Проиллюстрируем нечеткое множество «между 5 и 8 И (AND) около 4» (синяя линия).
- 36. 3. ДополнениеНечеткое множество В является дополнением нечеткого
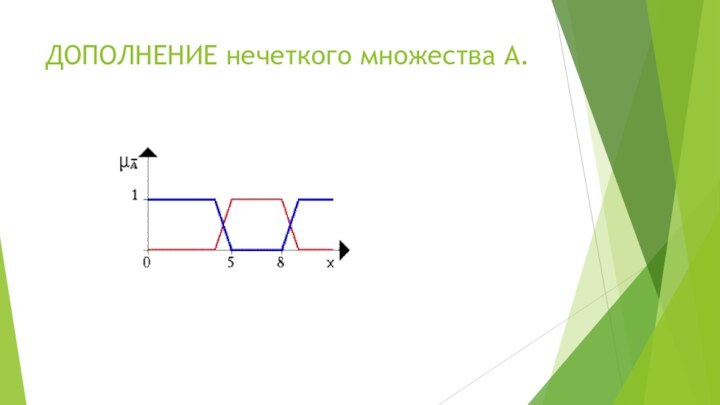
- 37. ДОПОЛНЕНИЕ нечеткого множества A.
- 38. 4. Разность.Разностью нечетких множеств является нечеткое множество с функцией принадлежностиОбозначается А\B
- 40. 5. Дизъюнктивная суммаДизъюнктивная сумма
- 41. Скачать презентацию
- 42. Похожие презентации
С = {0,04/молоко; 0,15/творог; 0,25/сливки; 0,35/ сыр; 0,40/сметана; 0,78/масло; 0,98/топленое масло} µс(х).








![Нечеткая логика Примеры нечетких множеств 1. Пусть E = {0,1,2,..,10}, M =[0,1]. Нечеткое множество](/img/tmb/14/1312379/5b53949f2e89478c5b174f954160d1bf-720x.jpg)















![Нечеткая логика Пусть M = [0,1] и A - нечеткое множество с элементами из](/img/tmb/14/1312379/adf91bbc245709eb447d280c3eacb7c3-720x.jpg)




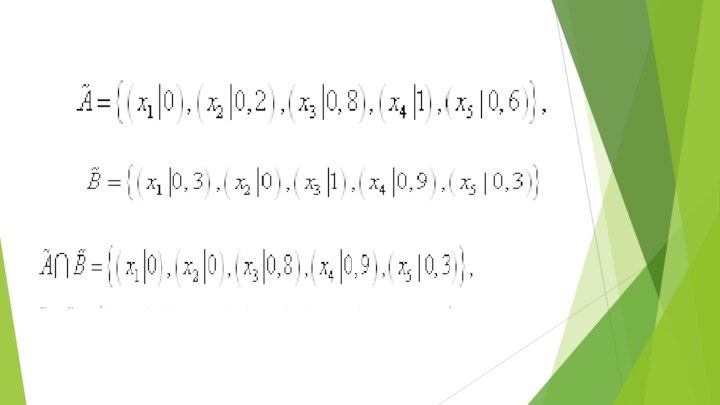






Слайд 5
Примеры записи нечеткого множества
Пусть E = {x1, x2,
x3, x4, x5 }, M = [0,1]; A -
нечеткое множество, для которогоµA(x1)=0,3; µA(x2)=0; µA(x3)=1; µA(x4)=0,5; µA(x5)=0,9.
Тогда A можно представить в виде: A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5 } или
A = 0,3/x1 + 0/x2 + 1/x3 + 0,5/x4 + 0,9/x5,
А =
Слайд 7 Рассмотрим нечеткое множество A , соответствующее понятию «расход
теплоносителя небольшой».
Объект x – расход теплоносителя, x0; x max
– множество физически возможных значений скорости изменения температуры.Эксперту предъявляются различные значения расхода теплоносителя x и задается вопрос: с какой степенью уверенности 0 ≤ μ A (x) ≤ 1 эксперт считает, что данный расход теплоносителя x небольшой.
При μ A (x) = 0 – эксперт абсолютно уверен, что расход теплоносителя x небольшой. При μ A (x) = 1 – эксперт абсолютно уверен, что расход теплоносителя x нельзя классифицировать как небольшой.
Слайд 10
Примеры нечетких множеств
1. Пусть E = {0,1,2,..,10}, M
=[0,1]. Нечеткое множество "несколько" можно определить таким образом:
"несколько"
= 0,5/3+0,8/4+1/5+1/6+0,8/7+0,5/8; ее характеристики: высота = 1, носитель={3,4,5,6,7,8}, точки перехода - {3,8}.
2. Пусть E = {Запорожец, Жигули, Мерседес,....} - множество марок автомобилей, а E' = [0,µ] - универсальное множество "стоимость", тогда на E' мы можем определить нечеткие множества типа: "для небогатых ", "для среднего класса", "престижные", с функциями принадлежности типа:
Имея эти функции и зная цены автомобилей из E в данный момент времени, определим на E' нечеткие множества с этими же названиями.
Так, например, нечеткое множество "для небогатых", заданное на универсальном множестве E = {Запорожец, Жигули, Мерседес,....} выглядит таким образом:
Слайд 11
Нечеткая переменная характеризуется тройкой , где
α
- наименование переменной,
X - универсальное множество (область определения α),
A
- нечеткое множество на X, описывающее ограничения (т.е. μ A(x)) на значения нечеткой переменной α.
Слайд 12
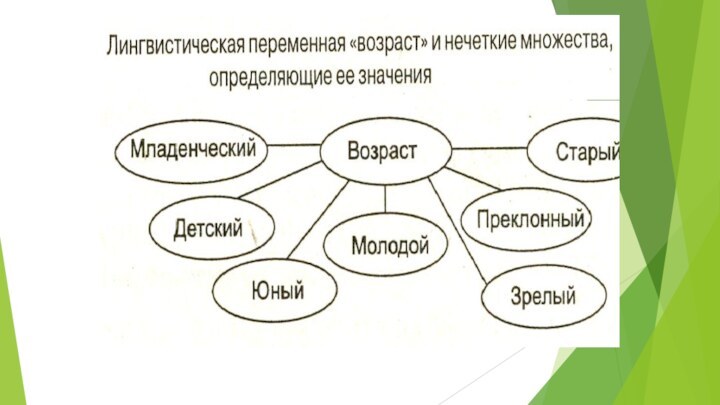
Лингвистической переменной называется набор , где
β -
наименование лингвистической переменной;
Т - множество ее значений (терм-множество), представляющих
собой наименования нечетких переменных, областью определения каждой из которых является множество X.Множество T называется базовым терм-множеством лингвистической переменной;
G - синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности, генерировать новые термы (значения). Множество TÈ G(T), где G(T) - множество сгенерированных термов, называется расширенным терм-множеством лингвистической переменной;
М - семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество.
Слайд 16 Пример: Пусть эксперт определяет толщину выпускаемого изделия с
помощью понятий "малая толщина", "средняя толщина" и "большая толщина",
при этом минимальная толщина равна 10 мм, а максимальная - 80 мм.Формализация такого описания может быть проведена с помощью следующей лингвистической переменной < β, T, X, G, M>, где
β - толщина изделия;
T - {"малая толщина", "средняя толщина", "большая толщина"};
X - [10, 80];
G - процедура образования новых термов с помощью связок "и", "или" и модификаторов типа "очень", "не", "слегка" и др. Например: "малая или средняя толщина", "очень малая толщина" и др.;
М - процедура задания на X = [10, 80] нечетких подмножеств А1="малая толщина", А2 = "средняя толщина", А3="большая толщина", а также нечетких множеств для термов из G(T) в соответствии с правилами трансляции нечетких связок и модификаторов "и", "или", "не", "очень", "слегка" и др. операции над нечеткими множествами вида: А Ç В, АÈ В, , CON А = А2 , DIL А = А0,5 и др.
Слайд 18
Преимущества нечетких систем
возможность оперировать нечеткими входными данными: например,
непрерывно изменяющиеся во времени значения (динамические задачи), значения, которые
невозможно задать однозначно (результаты статистических опросов, рекламные компании и т.д.);возможность нечеткой формализации критериев оценки и сравнения: оперирование критериями "большинство", "возможно", преимущественно" и т.д.;
возможность проведения качественных оценок как входных данных, так и выходных результатов: вы оперируете не только значениями данных, но и их степенью достоверности (не путать с вероятностью!) и ее распределением;
возможность проведения быстрого моделирования сложных динамических систем и их сравнительный анализ с заданной степенью точности: оперируя принципами поведения системы, описанными fuzzy-методами, вы во-первых, не тратите много времени на выяснение точных значений переменных и составление описывающих уравнений, во-вторых, можете оценить разные варианты выходных значений.
Слайд 19
Применение нечетких систем
CubiCalc 2.0 RTC - одна из
мощных коммерческих экспертных систем на основе нечеткой логики, позволяющая
создавать собственные прикладные экспертные системы ;CubiQuick - дешевая "университетская" версия пакета CubiCalc ;
RuleMaker - программа автоматического извлечения нечетких правил из входных данных ;
FuziCalc - электронная таблица с нечеткими полями, позволяющая делать быстрые оценки при неточных данных без накопления погрешности;
OWL - пакет, содержащий исходные тексты всех известных видов нейронных сетей, нечеткой ассоциативной памяти и т.д.
Слайд 20
Использование нечеткого управления рекомендуется...
для очень сложных процессов,
когда не существует простой математической модели
для нелинейных процессов
высоких порядков если должна производиться обработка (лингвистически сформулированных) экспертных знаний
Использование нечеткого управления не рекомендуется, если...
приемлемый результат может быть получен с помощью общей теории управления
уже существует формализованная и адекватная математическая модель
проблема не разрешима
Слайд 22 Фотоаппараты и видеокамеры используют нечеткую логику, чтобы реализовать
опыт фотографа в управлении этими устройствами. Например, компании Fisherи
Sanyo производят нечеткие логические видеокамеры, в которых применяется нечеткая фокусировка и стабилизация изображения.Компания Matsushita выпускает стиральную машину, в которой используются датчики и микропроцессоры с нечеткими алгоритмами управления. Датчики определяют цвет и вид одежды, степень загрязнения, а нечеткий микропроцессор выбирает наиболее подходящую программу стирки из 600 доступных комбинаций температуры воды, количества стирального порошка и времени стирки.
Компания Mitsubishi выпустила первый в мире автомобиль, где управление каждой системой основано на нечеткой логике. Эта же компания производит «нечеткий» кондиционер, который управляет изменением температуры и влажности в помещении согласно человеческому восприятию степени комфорта.
Компания Nissan разработала «нечеткую» автоматическую трансмиссию и «нечеткую» противоскользящую тормозную систему и реализовала их в одном из своих автомобилей повышенной комфортности.
Слайд 23 Японский город Сендай имеет метрополитен с 16 станциями,
который управляется нечетким компьютером. При этом нечеткий компьютер регулирует
процессы ускорения и торможения поездов метро, делая на 70 % меньше ошибок, чем соответствующий человек-оператор.На фондовом рынке Токио используется несколько трейдерных систем, основанных на нечеткой логике, которые превосходят по скоростным и динамическим характеристикам традиционные информационные системы.
В Японии имеются также «нечеткие» системы управления уличным движением, «нечеткие» тостеры, «нечеткие» рисовые печи, «нечеткие» пылесосы и многие другие бытовые технические устройства.
Слайд 24 Автоматическое управление воротами плотины на гидроэлектростанциях (Tokio Electric
Pow.)
Упрощенное управление роботами
(Hirota, Fuji Electric, Toshiba, Omron)
Наведение телекамер при трансляции спортивных событий (Omron)
Замена экспертов при анализе работы биржи (Yamaichi, Hitachi)
Предотвращение нежелательных температурных флуктуаций в системах кондиционирования воздуха (Mitsubishi, Sharp)
Эффективное и стабильное управление автомобильными двигателями (Nissan)
Управление экономичной скоростью автомобилей (Nissan, Subaru)
Слайд 25 Улучшение эффективности и оптимизация промышленных систем управления (Aptronix,
Omron, Meiden, Sha, Micom, Mitsubishi, Nisshin-Denki, Oku-Electronics)
Позиционирование приводов
в производстве полупроводников wafer-steppers
(Canon) Оптимизированное планирование автобусных расписаний (Toshiba, Nippon-System, Keihan-Express)
Системы архивации документов (Mitsubishi Elec.)
Системы прогнозирования землетрясений (Inst. of Seismology Bureau of Metrology, Japan)
Медицина: диагностика рака (Kawasaki Medical School)
Сочетание методов нечеткой логики и нейронных сетей (Matsushita)
Распознавание рукописных символов в карманных компьютерах (записных книжках) (Sony)
Слайд 26
Распознавание движения изображения в видеокамерах
(Canon, Minolta)
Автоматическое
управление двигателем пылесосов с автоматическим определением типа поверхности и
степени засоренности (Matsushita)Управление освещенностью в камкодерах (Sanyo)
Компенсация вибраций в камкодерах (Matsushita)
Однокнопочное управление стиральными машинами (Matsushita, Hitatchi)
Распознавание рукописных текстов, объектов, голоса (CSK, Hitachi, Hosai Univ., Ricoh)
Вспомагательные средства полета вертолетов (Sugeno)
Моделирование судебных процессов (Meihi Gakuin Univ, Nagoy Univ.)
Слайд 27
САПР производственных процессов
(Aptronix, Harima, Ishikawajima-OC Engeneering)
Управление
скоростью линий и температурой при производстве стали (Kawasaki Steel,
New-Nippon Steel, NKK)Управление метрополитенами для повышения удобства вождения, точности остановки и экономии энергии (Hitachi)
Оптимизация потребления бензина в автомобилях (NOK, Nippon Denki Tools)
Повышение чувствительности и эффективности управления лифтами (Fujitec, Hitachi, Toshiba)
Повышение безопасности ядерных реакторов (Hitachi, Bernard, Nuclear Fuel div.)
Слайд 29 Пусть M = [0,1] и A - нечеткое
множество с элементами из универсального множества E и множеством
принадлежностей M.Величина µA(x) называется высотой нечеткого множества A. Нечеткое множество A нормально, если его высота равна 1, т.е. верхняя граница его функции принадлежности равна 1 (µA(x)=1). При µA(x) <1 нечеткое множество называется субнормальным.
Нечеткое множество пусто, если µ A(x)=0.
Нечеткое множество унимодально, если µ A(x)=1 только на одном x из E.
Элементы xE, для которых µA(x)=0,5 называются точками перехода множества A.
Слайд 30
μС(х)=max{μA(х), μB(х)}, х
1. Объединением нечетких множеств A и
B называется нечеткое множество C с функцией принадлежности вида
X
Объединение соответствует логической связке «ИЛИ»
Обозначается символом
Слайд 33
4. Пересечение
Пересечением нечетких множеств А и В в
Х называется нечеткое множество С с функцией принадлежности вида
μС(х)=min{μA(х), μB(х)}, х
X
Пересечение соответствует логической связке «И»
Обозначается символом
Слайд 36
3. Дополнение
Нечеткое множество В является дополнением нечеткого множества
А, если для любого х
Х выполняется условие
Обозначается
илиДополнение А = {(х1|1), (х2|0,8), (х3|0,2),(х4|0),(х5|0,4)}





























