- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Парадчетырех-угольников
Содержание
- 2. Проверка домашнего задания
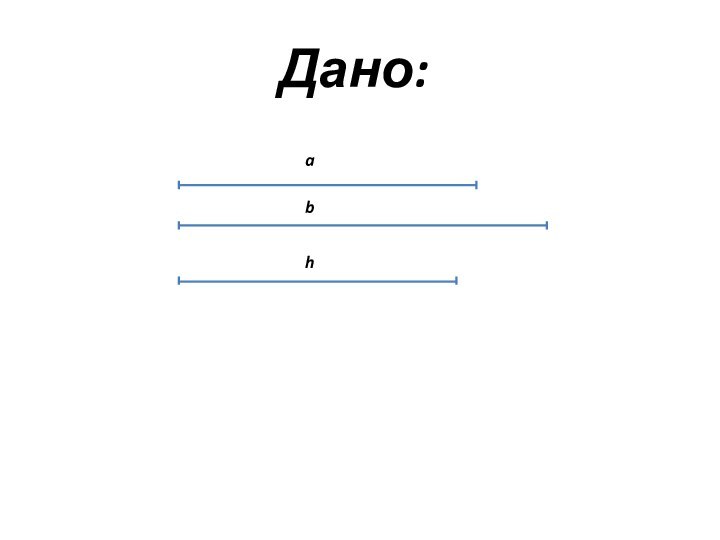
- 3. № 139Построить равнобедренную трапецию по боковой стороне a, большему основанию b и высоте h трапеции
- 4. Дано:
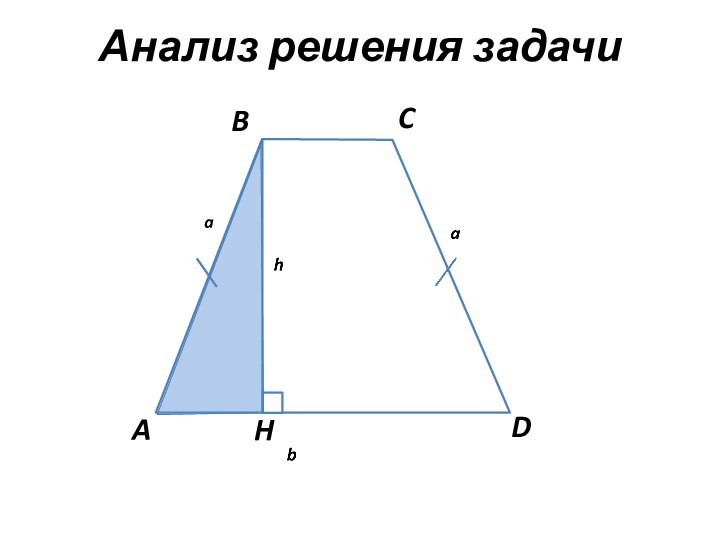
- 5. Анализ решения задачиaADBCH
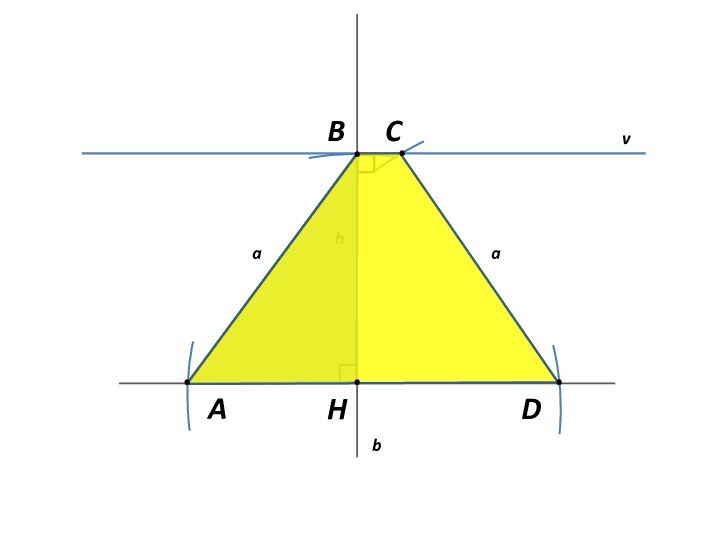
- 6. HBhAaDabCv.....
- 7. Построение
- 8. Доказательство
- 9. Задача имеет единственное решение, если a>h Исследование
- 10. ЧетырехугольникПараллелограммПрямоугольникРомбКвадратТрапецияРавнобедреннаяПрямоугольная
- 11. Свойства четырехугольниковПротивоположные стороны равны
- 12. Свойства четырехугольниковДиагонали взаимно перпендикулярны
- 13. Свойства четырехугольниковДиагонали равны
- 14. Свойства четырехугольниковДиагонали равныи взаимно перпендикулярны
- 15. Свойства четырехугольниковДиагонали являются биссектрисами углов
- 16. Тренинг в парах «Признаки четырехугольников»
- 17. Структура теоремыУсловиеЗаключениеЕслиТо
- 18. ЧетырехугольникПараллелограммПрямоугольникРомбКвадрат
- 19. Проверочный тест
- 20. № 1Один из углов параллелограмма на 20°
- 21. № 2Периметр ромба равен 20 см. Если
- 22. № 3Одна из диагоналей прямоугольника равна 6
- 23. №4Если в равнобедренной трапеции острый угол равен
- 24. № 5Если в прямоугольной трапеции ее основания
- 25. № 1Один из углов параллелограмма на 20°
- 26. № 2Периметр ромба равен 20 см. Если
- 27. № 3Одна из диагоналей прямоугольника равна 6
- 28. №4Если в равнобедренной трапеции острый угол равен
- 29. № 5Если в прямоугольной трапеции ее основания
- 30. Интересные и полезные дополнительные сведения о четырехугольниках
- 31. Свойства параллелограмма
- 32. Биссектрисы противоположных углов параллелограмма лежат на параллельных прямыхABCDHO12345
- 33. Биссектрисы соседних углов параллелограмма пересекаются под прямым углом
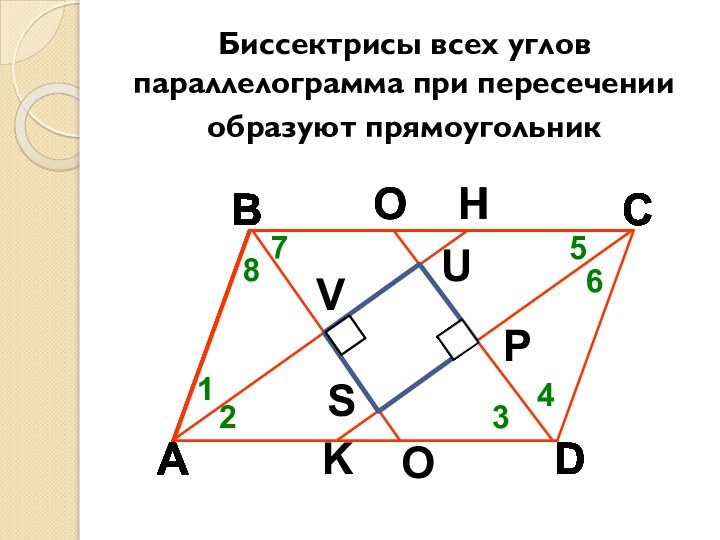
- 34. Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник
- 35. Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны
- 36. Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм
- 37. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольникBCDH123
- 38. Интересные и полезные дополнительные сведения о четырехугольниках
- 39. Интересные и полезные дополнительные сведения о прямоугольниках
- 40. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон ABCDabc
- 41. Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности (радиус равен полудиагонали)ABCDO
- 42. Интересные и полезные дополнительные сведения о четырехугольниках
- 43. Фигура ромб в белорусском орнаменте
- 45. Ромб в славянской культуре
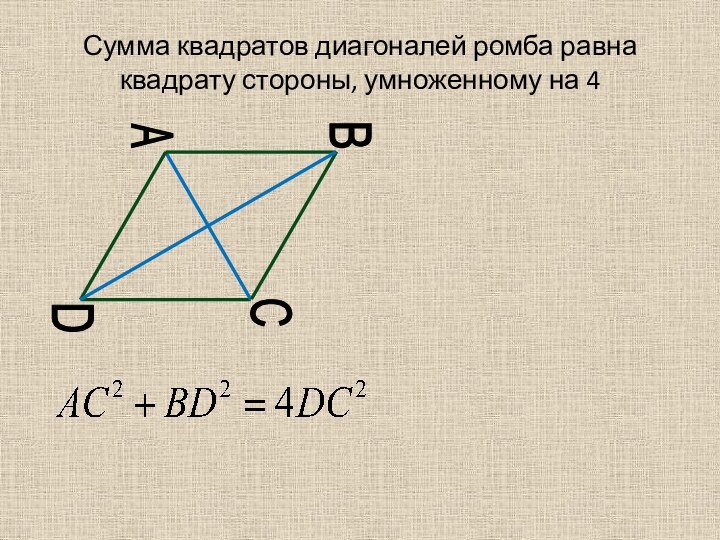
- 47. Сумма квадратов диагоналей ромба равна квадрату стороны, умноженному на 4ABCD
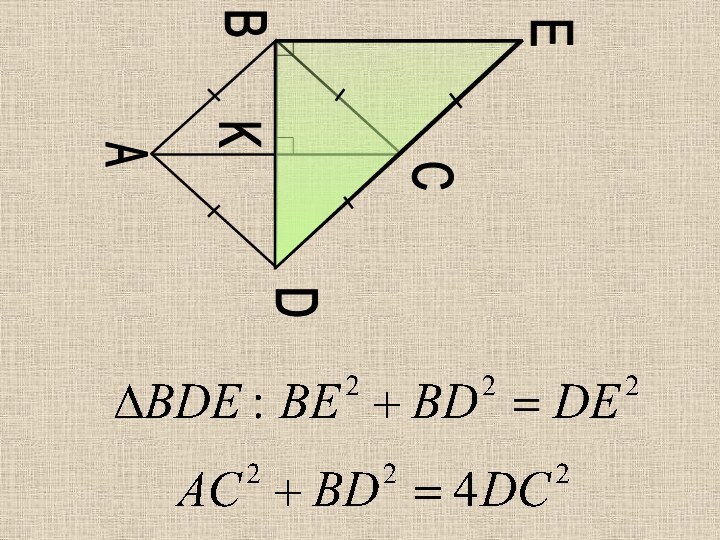
- 48. ABCDEK
- 49. Интересные и полезные дополнительные сведения о четырехугольниках
- 50. Cвойства трапеции
- 51. ABCDEAE= 0,5(AD-BC)ED=0,5(BC+AD)В равнобедренной трапеции высота, опущенная из
- 52. ДоказательствоABCDETПусть AE=TD=x, ET=BC=aXaaXТогда AE= 0,5(AD-BC)= 0,5(2x+a-a)=x
- 53. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме основанийBH=0,5(AD+BC)ABCD
- 54. Формула БураковаВ трапеции отрезок, параллельный основаниям и
- 55. Решение задач на построение четырехугольников с помощью циркуля и линейки
- 56. Этапы решения задач на построение
- 57. Группа №1Постройте трапециюпо двум диагоналямm и n
- 58. № 149Постройте ромб по стороне и сумме
- 59. Скачать презентацию
- 60. Похожие презентации
Проверка домашнего задания














































Слайд 20
№ 1
Один из углов параллелограмма на 20° больше
другого. Тогда больший угол параллелограмма равен:
1)80°; 2)100°;
3)130°; 4)120°.
Слайд 21
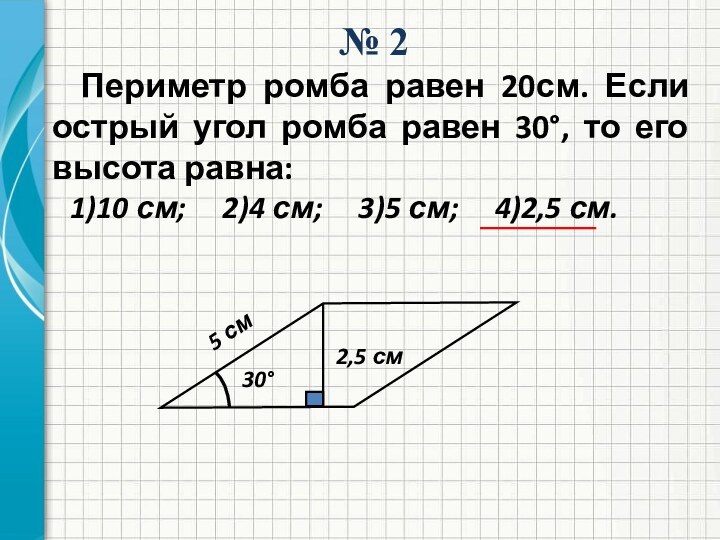
№ 2
Периметр ромба равен 20 см. Если острый
угол ромба равен 30°, то его высота равна:
1)10 см;
2)4 см; 3)5 см; 4)2,5 см.
Слайд 22
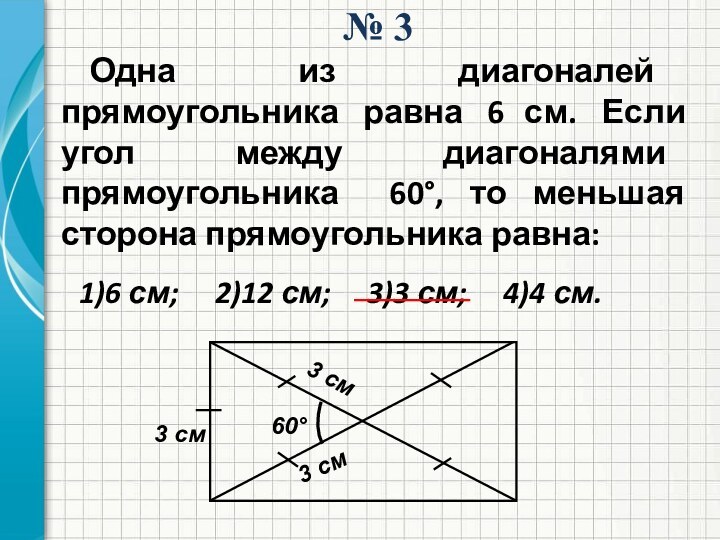
№ 3
Одна из диагоналей прямоугольника равна 6 см.
Если угол между диагоналями прямоугольника 60°, то меньшая сторона
прямоугольника равна:1)6 см; 2)12 см; 3)3 см; 4)4 см.
Слайд 23
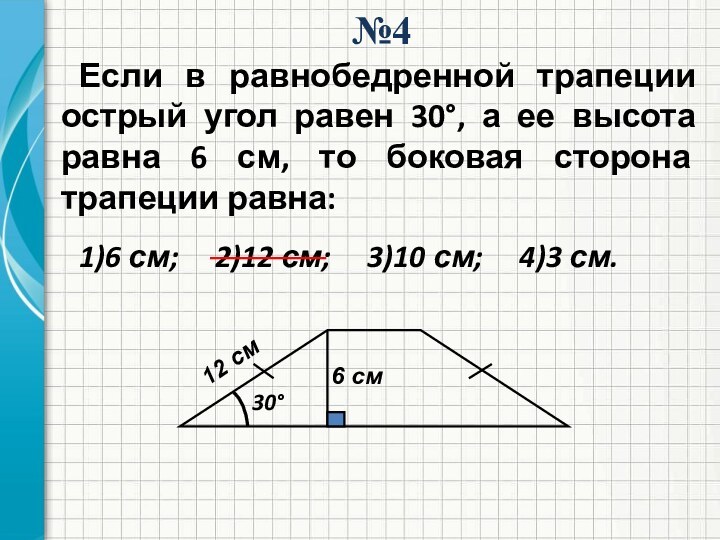
№4
Если в равнобедренной трапеции острый угол равен 30°,
а ее высота равна 6 см, то боковая сторона
трапеции равна:1)6 см; 2)12 см; 3)10 см; 4)3 см.
Слайд 24
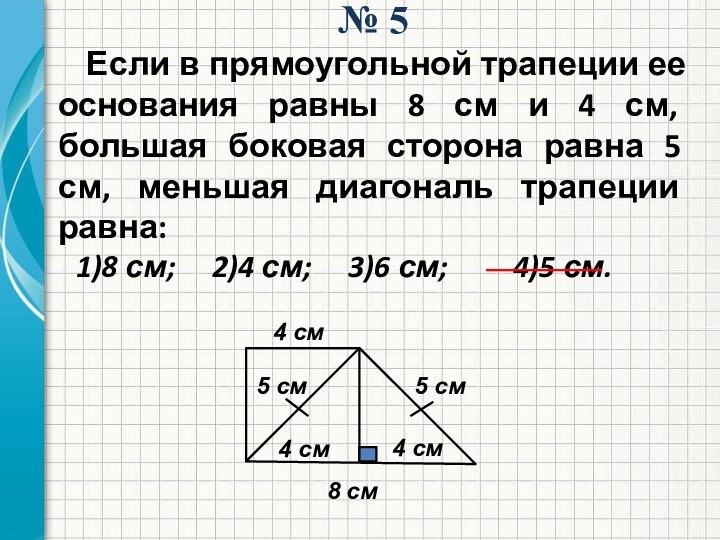
№ 5
Если в прямоугольной трапеции ее основания равны
8 см и 4 см, большая боковая сторона равна
5 см, меньшая диагональ трапеции равна:1)8 см; 2)4 см; 3)6 см; 4)5 см.
Слайд 25
№ 1
Один из углов параллелограмма на 20° больше
другого. Тогда больший угол параллелограмма равен:
1)80°; 2)100°;
3)130°; 4)120°.х
х+20°
х+ х+20°=180°, х=80°
Слайд 26
№ 2
Периметр ромба равен 20 см. Если острый
угол ромба равен 30°, то его высота равна:
1)10 см;
2)4 см; 3)5 см; 4)2,5 см.30°
5 см
2,5 см
Слайд 27
№ 3
Одна из диагоналей прямоугольника равна 6 см.
Если угол между диагоналями прямоугольника 60°, то меньшая сторона
прямоугольника равна:1)6 см; 2)12 см; 3)3 см; 4)4 см.
60°
3 см
3 см
3 см
Слайд 28
№4
Если в равнобедренной трапеции острый угол равен 30°,
а ее высота равна 6 см, то боковая сторона
трапеции равна:1)6 см; 2)12 см; 3)10 см; 4)3 см.
6 см
30°
12 см
Слайд 29
№ 5
Если в прямоугольной трапеции ее основания равны
8 см и 4 см, большая боковая сторона равна
5 см, меньшая диагональ трапеции равна:1)8 см; 2)4 см; 3)6 см; 4)5 см.
4 см
8 см
5 см
4 см
4 см
5 см
Слайд 36 Если в параллелограмме соединить противоположные вершины с серединами
противоположных сторон, то получится еще один параллелограмм
Слайд 41 Около любого прямоугольника можно описать окружность, причем диагональ
прямоугольника равна диаметру описанной окружности (радиус равен полудиагонали)
A
B
C
D
O
Слайд 51
A
B
C
D
E
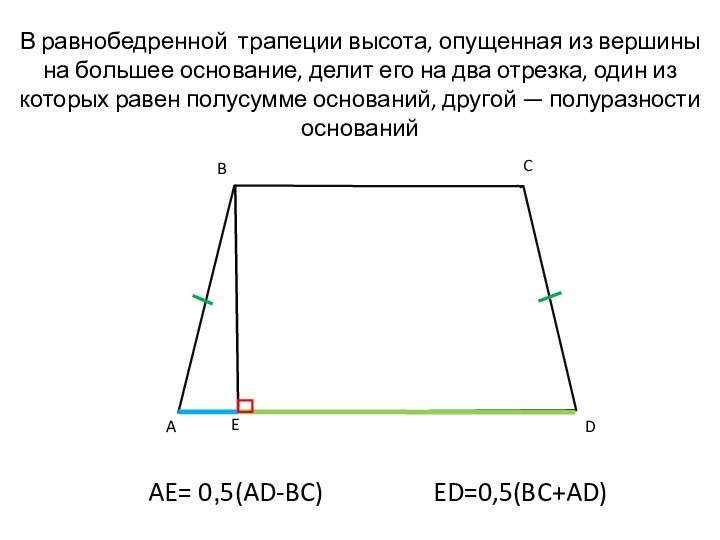
AE= 0,5(AD-BC)
ED=0,5(BC+AD)
В равнобедренной трапеции высота, опущенная из вершины
на большее основание, делит его на два отрезка, один
из которых равен полусумме оснований, другой — полуразности оснований
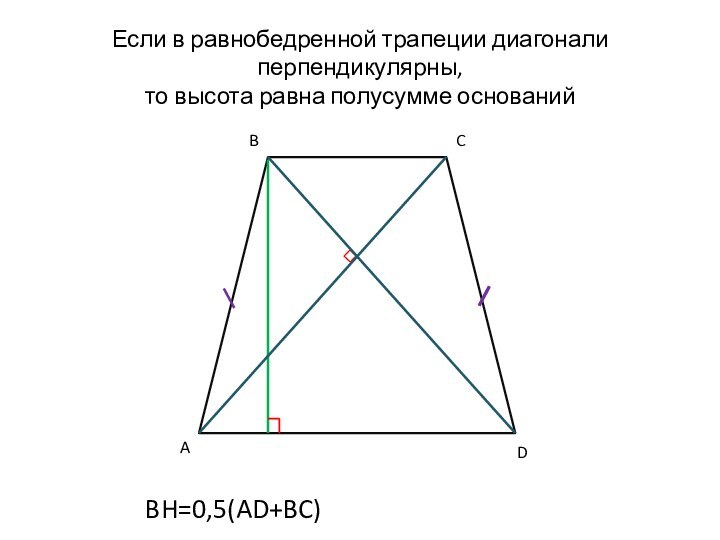
Слайд 53
Если в равнобедренной трапеции диагонали перпендикулярны,
то высота
равна полусумме оснований
BH=0,5(AD+BC)
A
B
C
D
Слайд 54
Формула Буракова
В трапеции отрезок, параллельный основаниям и проходящий
через точку пересечения диагоналей, равен удвоенному произведению его оснований
на сумму оснований и точкой пересечения делится пополамA
B
C
D
F
H
O
FH=2ab(a+b),
a
b
FO=OH
Слайд 57
Группа №1
Постройте трапецию
по двум диагоналям
m и n
и
основаниям
a и b
Группа №2
Постройте трапецию
по боковым сторонам
х и
уи основаниям
a и b





























