- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Параметрический тест Гольдфельда-Квондта
Содержание
- 2. 1-й шаг Ранжируем наблюдения в порядке возрастания значений независимой переменной .
- 3. 2-й шаг Выбираем C центральных наблюдений переменной
- 4. 3-й шаг Строим две эконометрические модели на основе
- 5. 4-й шаг Рассчитываем суммы квадратов отклонений
- 6. 5-й шаг Рассчитываем значение критерия (соответствует F-распределению с
- 7. Если
- 8. Проранжируем выборку по возрастанию численности проживающих
- 10. Выберем число
- 12. Строим уравнения регрессии, находим отклонения, рассчитываем их суммы квадратов
- 15. Вывод: имеет место гомоскедастичность отклонений модели
- 16. Непараметрический тест Гольдфельда-Квондта В основе теста лежит
- 18. Тест Глейсера 1-й шаг Рассчитываются параметры уравнения регрессии и находятся величины отклонений
- 19. 2-й шаг Строятся уравнения регрессии, увязывающие модули остатков и фактор пропорциональности
- 20. Выбирается та модель, которая наиболее точно описывает
- 21. Тест Бреуша-Пэйгана Осуществляет попытку определить гетероскедастичность путем
- 22. 1-й шаг Находим отклонения на основе построенного уравнения регрессии
- 23. 2-й шаг Строим вторичное уравнение регрессии. Зависимая переменная
- 24. 3-й шаг Проверяем статистическую значимость уравнения, формулируя гипотезы Рассчитываем статистику
- 25. Для больших по размеру выборок
- 26. Если
- 27. Тест Уайта В качестве независимых переменных (факторов
- 28. 1-й шаг Находим отклонения наблюдаемых значений зависимой переменной от расчетных
- 29. 2-й шаг Строим вторичное уравнение регрессии
- 30. 3-й шаг Проверяем общую значимость уравнения с помощью
- 31. Если , то гипотеза об отсутствии гетероскедастичности остатков отвергается
- 32. Обобщенный метод наименьших квадратов (метод Эйткена) Пусть модель описывается уравнением и имеет дисперсию остатков, которая описывается выражением
- 33. Фактор пропорциональности представлен в
- 34. Если и ,то
- 35. Если и ,то
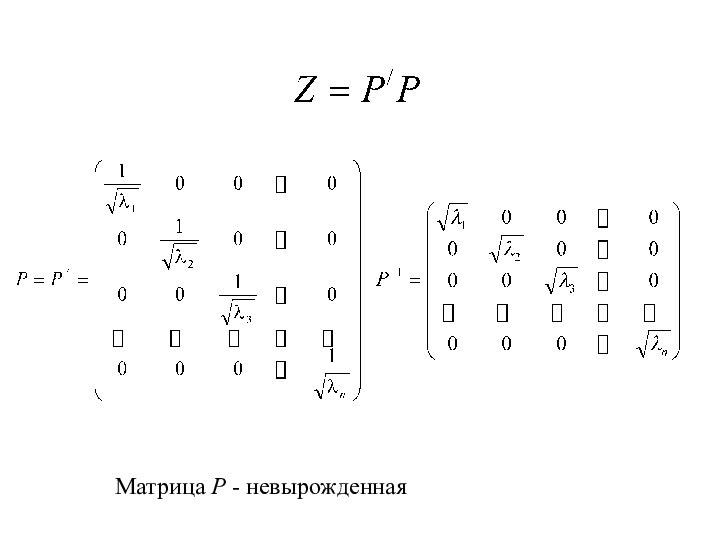
- 36. Матрица Р - невырожденная
- 37. Используя соотношение
- 39. Используя выражение
- 40. Дисперсионно-ковариационная матрица Вектор оценок модели рассчитывается так:
- 41. Несмещенная оценка дисперсии остатков
- 42. Разложим общую сумму квадратов на сумму квадратов
- 43. и дисперсию остатковЕсли имеет место система соотношений
- 44. где
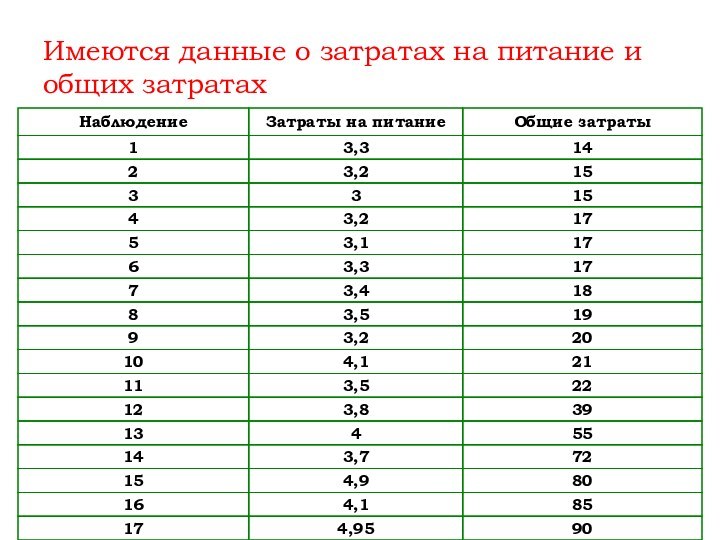
- 45. Имеются данные о затратах на питание и общих затратах
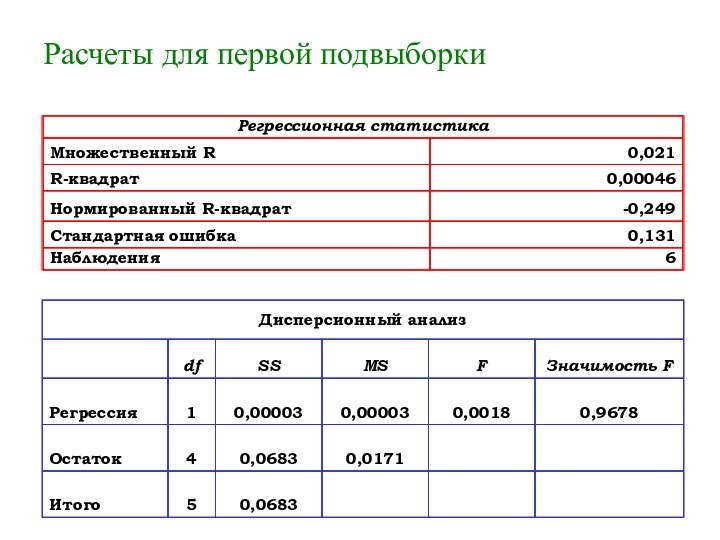
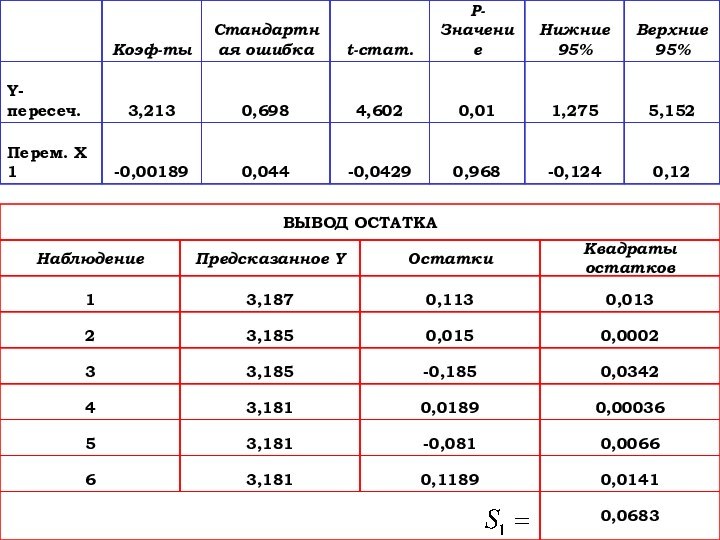
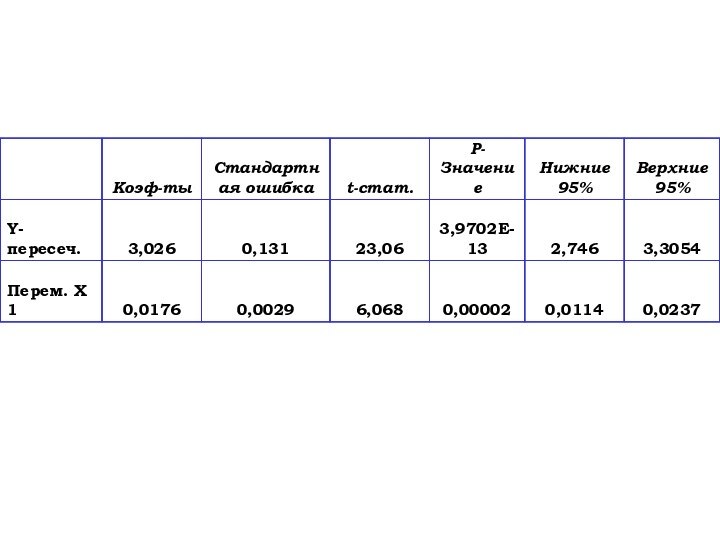
- 47. Расчеты для первой подвыборки
- 48.
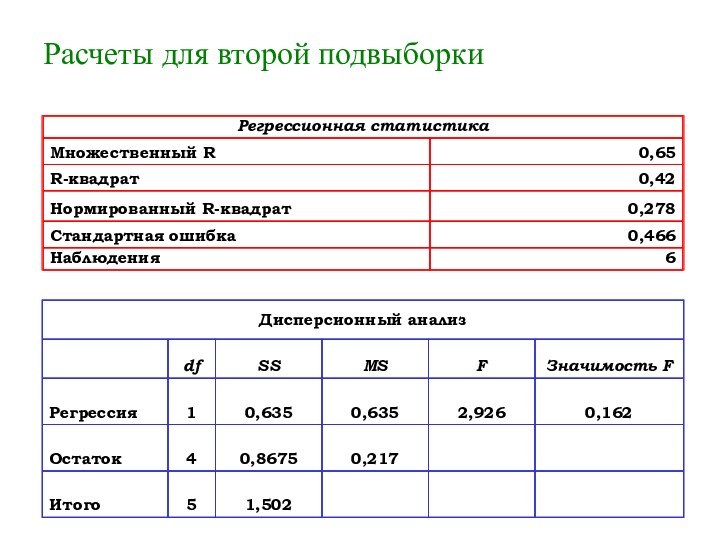
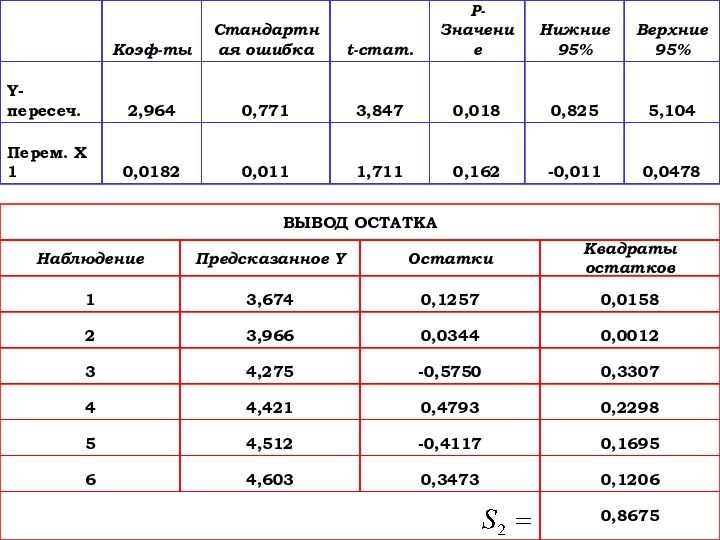
- 49. Расчеты для второй подвыборки
- 50.
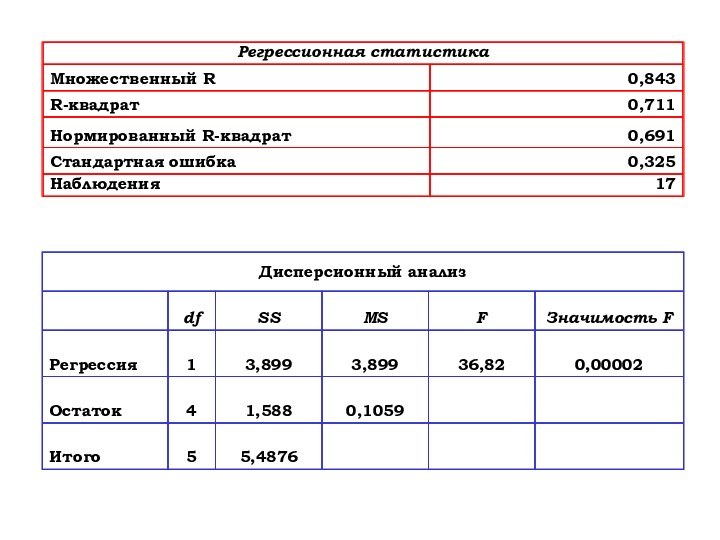
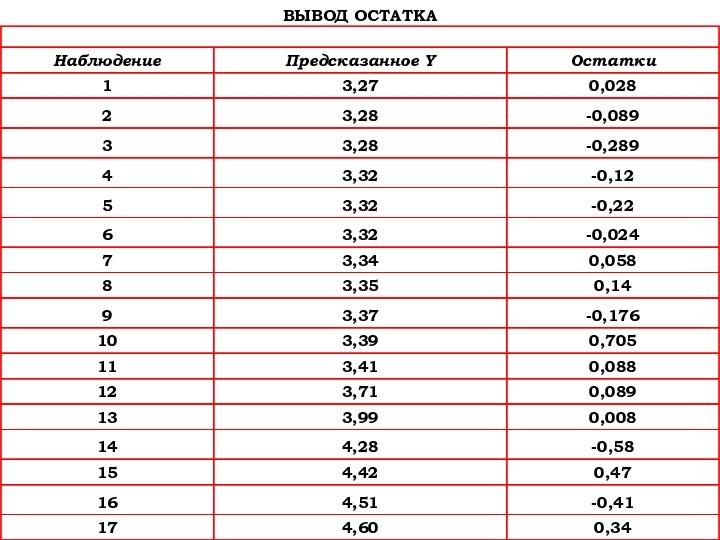
- 51. Имеет место гетероскедастичностьПрименим метод 1МНК
- 56. Найдем произведение Рассчитаем произведение Обратим полученное выражение
- 57. Скачать презентацию
- 58. Похожие презентации
1-й шаг Ранжируем наблюдения в порядке возрастания значений независимой переменной .








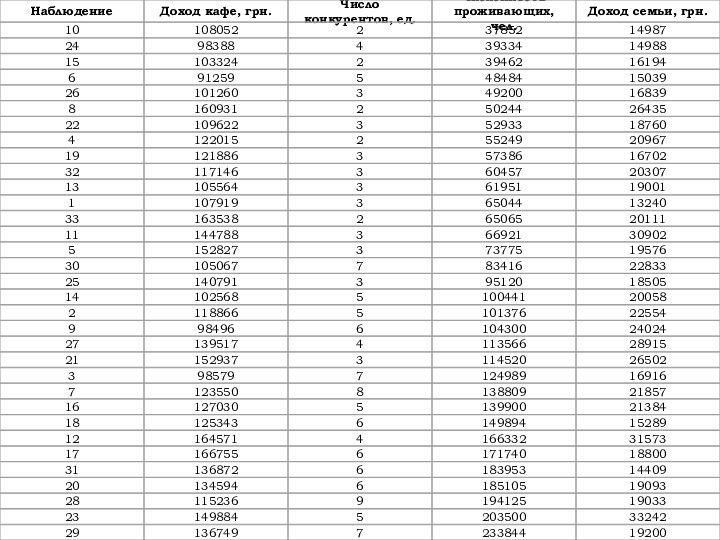




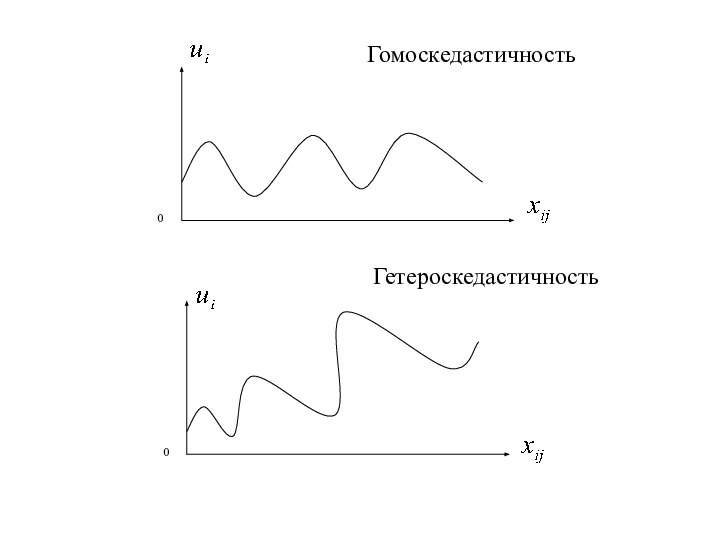
















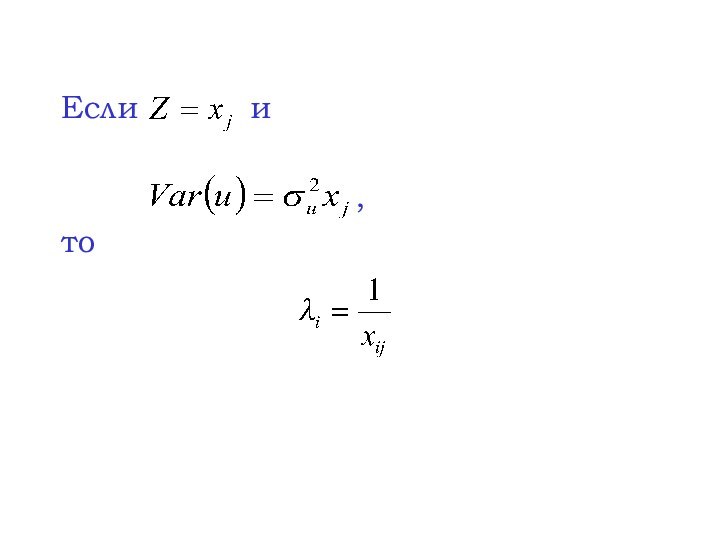
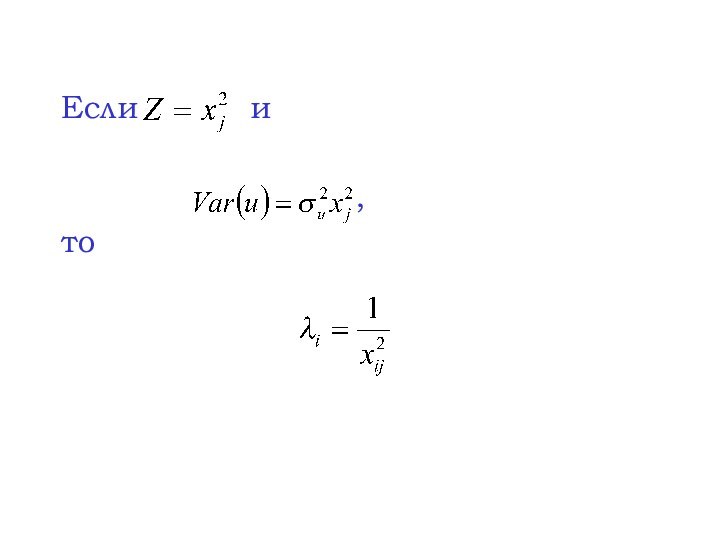

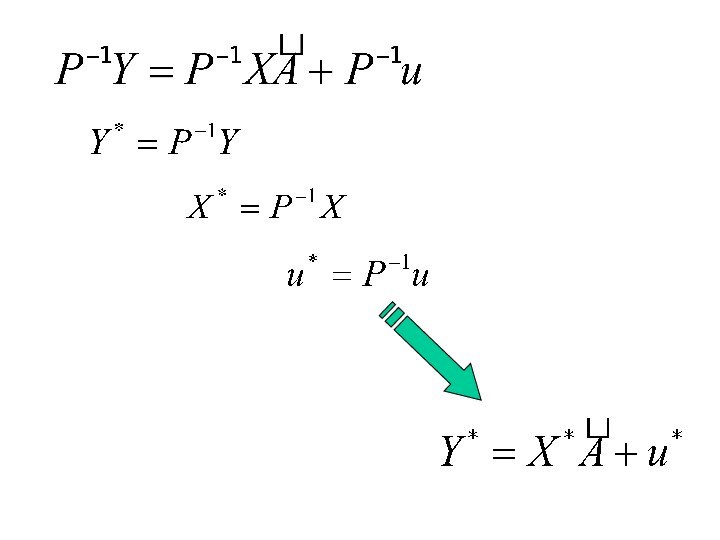









Слайд 3
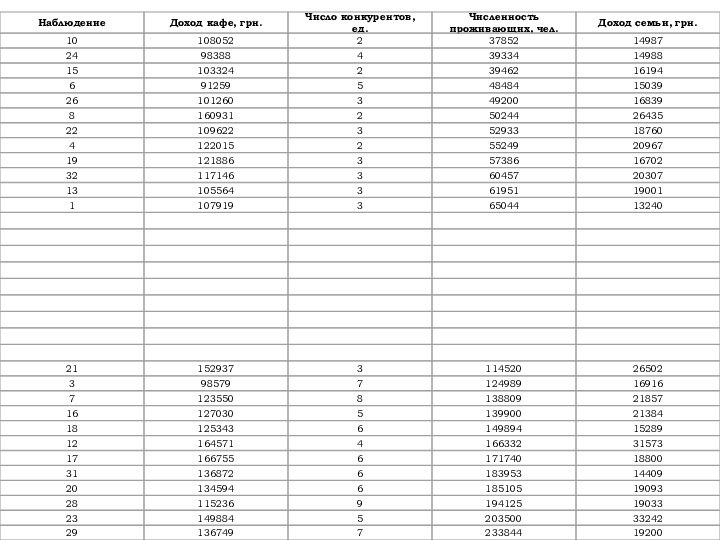
2-й шаг
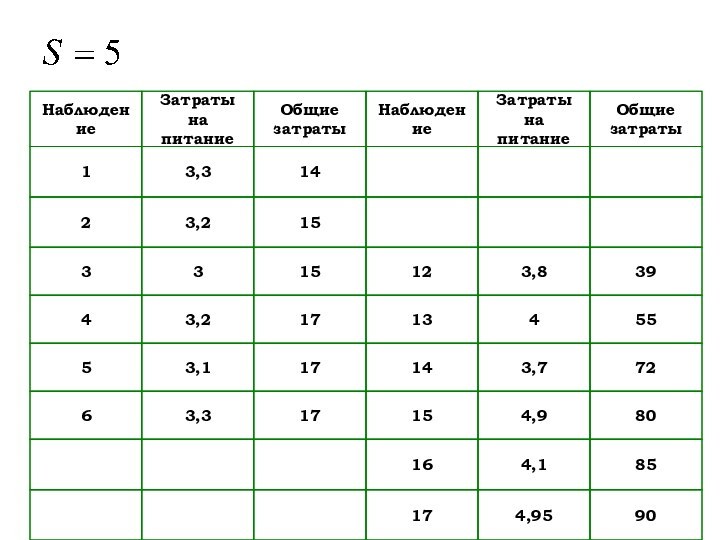
Выбираем C центральных наблюдений переменной и
исключаем их из выборки. Число C обычно принимают равным
от одной четвертой до одной трети общего числа наблюдений. Остаток наблюдений делится на две подвыборки, первая из которых состоит из наименьших значений переменной, вторая – из наибольших.
Слайд 4
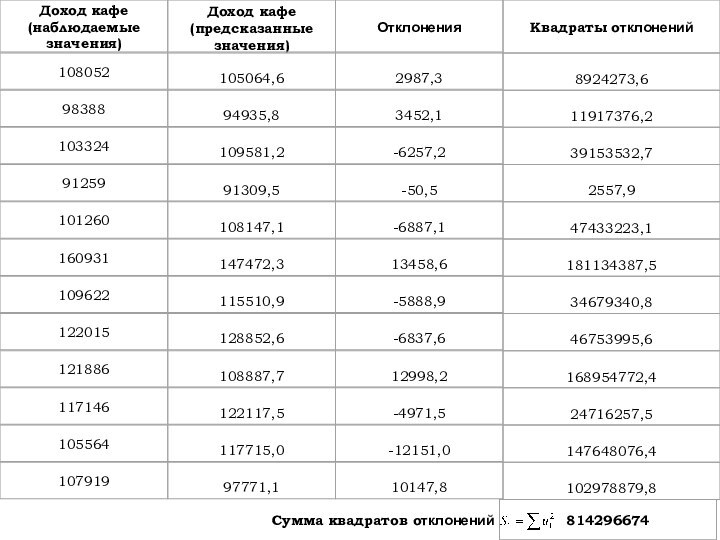
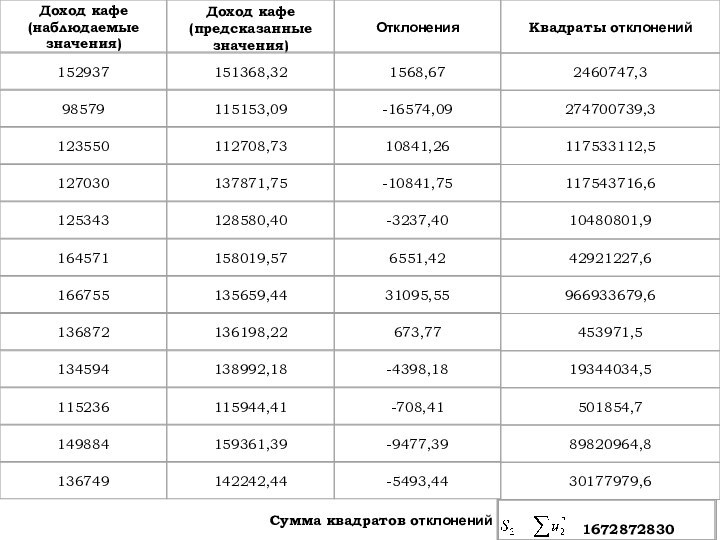
3-й шаг
Строим две эконометрические модели на основе каждой
из подвыборок, содержащих по
наблюдений
Слайд 6
5-й шаг
Рассчитываем значение критерия
(соответствует F-распределению с числом
степеней свободы
и уровнем значимости )
Слайд 16
Непараметрический тест Гольдфельда-Квондта
В основе теста лежит оценка
числа вершин величины остатков, получаемых после упорядочения наблюдений переменной
. Оценка осуществляется визуально путем анализа графика изменения остатков при изменении значений переменной .
Слайд 18
Тест Глейсера
1-й шаг
Рассчитываются параметры уравнения регрессии
и находятся величины отклонений
Слайд 19
2-й шаг
Строятся уравнения регрессии, увязывающие модули остатков
и фактор пропорциональности
Слайд 20 Выбирается та модель, которая наиболее точно описывает связь
между рассматриваемыми величинами
Если оба параметра и
являются значимыми (т.е. и ), то имеет место смешанная гетероскедастичность. Если , а , то – чистая
Слайд 21
Тест Бреуша-Пэйгана
Осуществляет попытку определить гетероскедастичность путем оценки
общей значимости вторичного уравнения регрессии, построенного на основе квадратов
отклонений зависимой переменной и сразу нескольких факторов пропорциональности
Слайд 23
2-й шаг
Строим вторичное уравнение регрессии.
Зависимая переменная –
квадраты отклонений. Независимые переменные – те из основной модели,
которые влияют на вариацию отклонений число факторов, определяющих вариацию отклонений
Слайд 24
3-й шаг
Проверяем статистическую значимость уравнения, формулируя гипотезы
Рассчитываем
статистику
Слайд 25 Для больших по размеру выборок
имеет -распределение с числом степеней свободы, равным
и уровнем значимости .
Слайд 26
Если
,
то нулевая гипотеза отвергается и уравнение считается значимым.
Т.о. делается вывод о наличии гетероскедастичности
Слайд 27
Тест Уайта
В качестве независимых переменных (факторов пропорциональности)
выступают все исходные независимые переменные, их квадраты и попарные
произведения
Слайд 30
3-й шаг
Проверяем общую значимость уравнения с помощью критерия
Рассчитываем
статистику , где
нескорректированный коэффициент детерминации, которая имеет -распределение с числом степеней свободы, равным числу угловых коэффициентов модели, и уровнем значимости
Слайд 32
Обобщенный метод наименьших квадратов (метод Эйткена)
Пусть модель
описывается уравнением
и имеет дисперсию остатков, которая описывается выражением
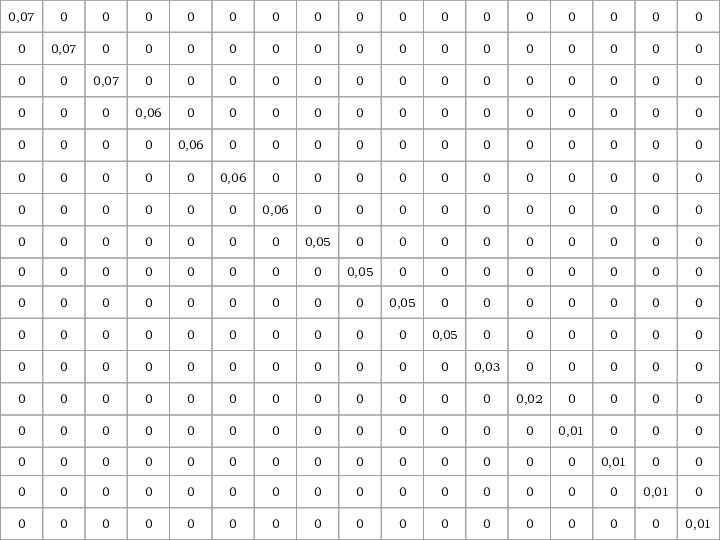
Слайд 33 Фактор пропорциональности представлен в виде
симметричной, положительно определенной матрицы
Диагональные элементы определяют пропорции изменения дисперсий
в зависимости от наблюдения объясняющей переменной Слайд 42 Разложим общую сумму квадратов на сумму квадратов регрессии
и остатков
Рассчитаем общую дисперсию
,дисперсию, объясняемую регрессией
Слайд 44 где известная
симметричная положительно определенная матрица, то вектор
рассчитывается как,
а дисперсионно-ковариационная матрица определяется из выражения





























