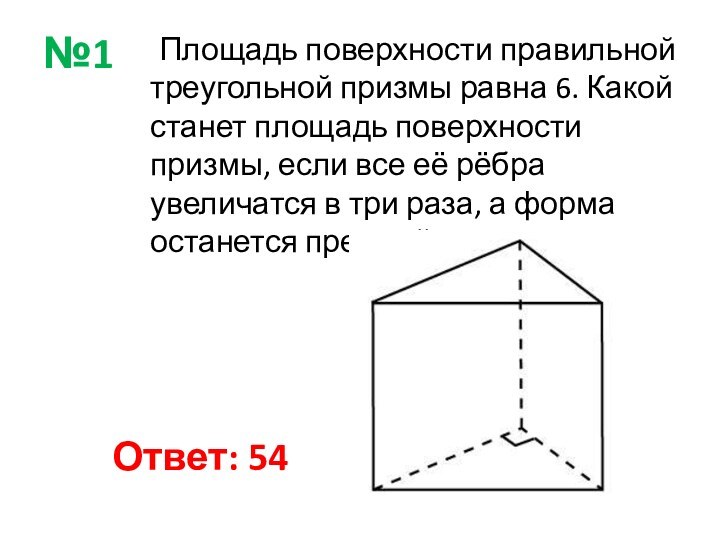
станет площадь поверхности призмы, если все её рёбра увеличатся
в три раза, а форма останется прежней?Ответ: 54
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

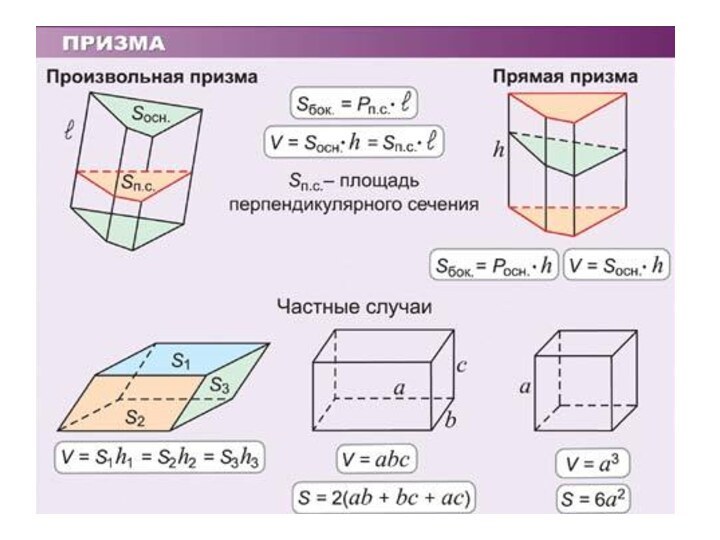
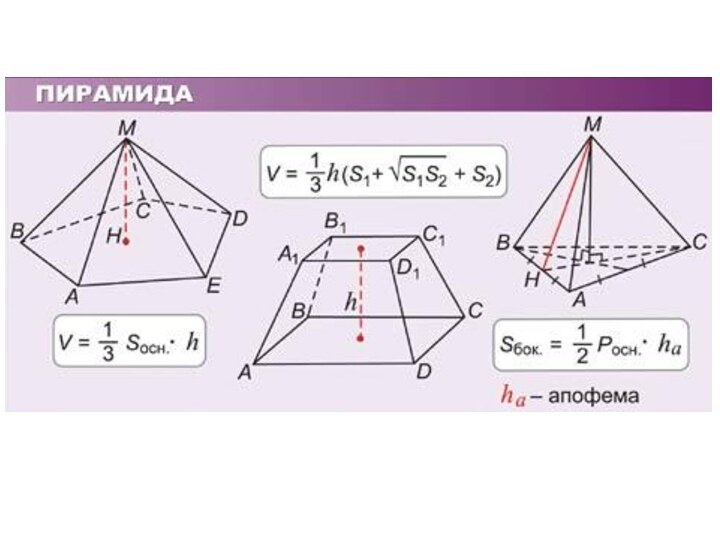
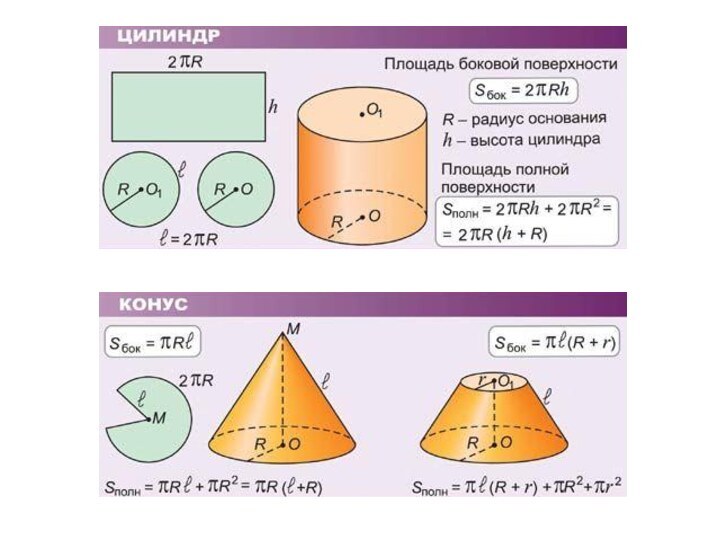
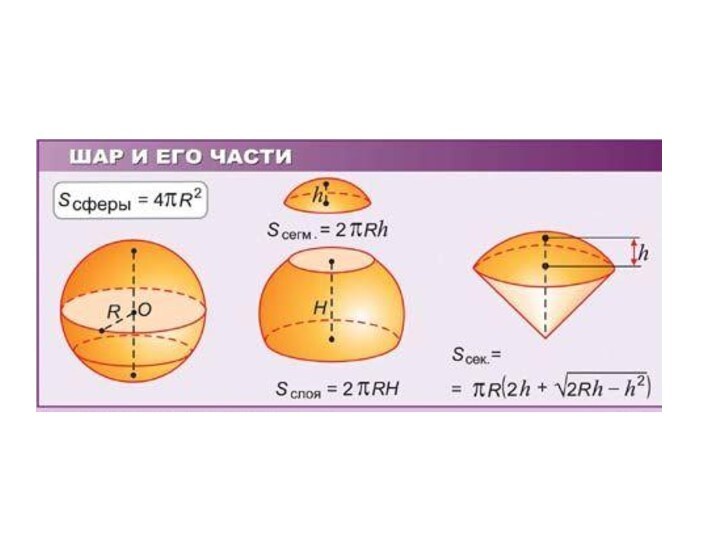

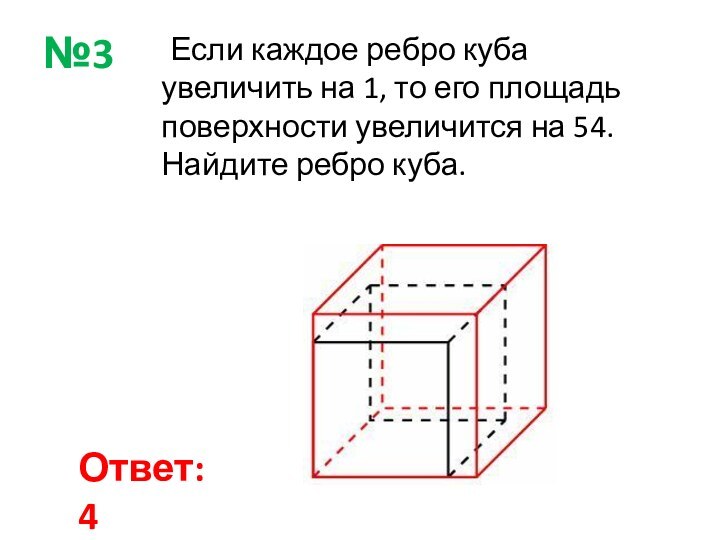

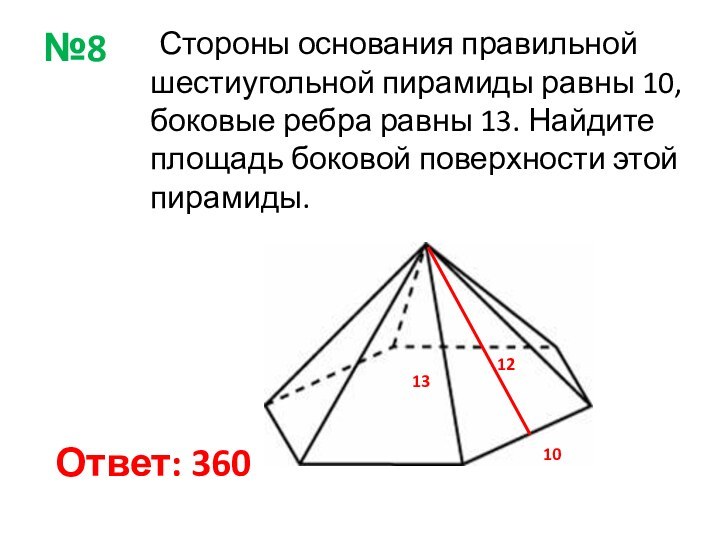
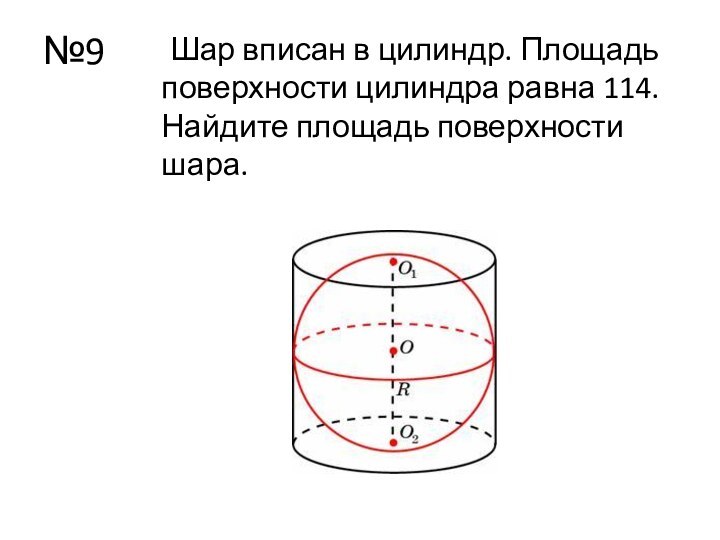


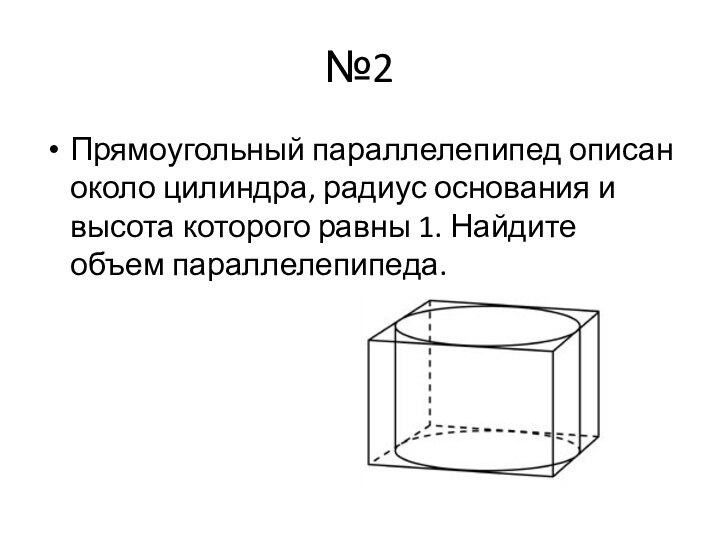
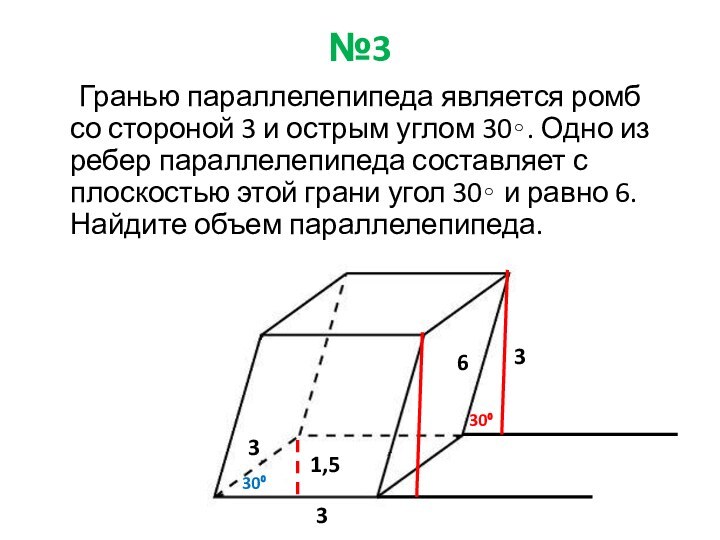
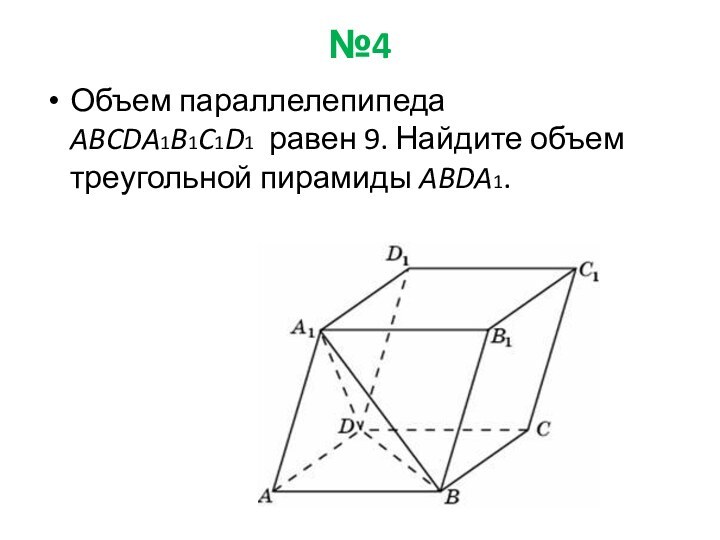


Ответ: 54
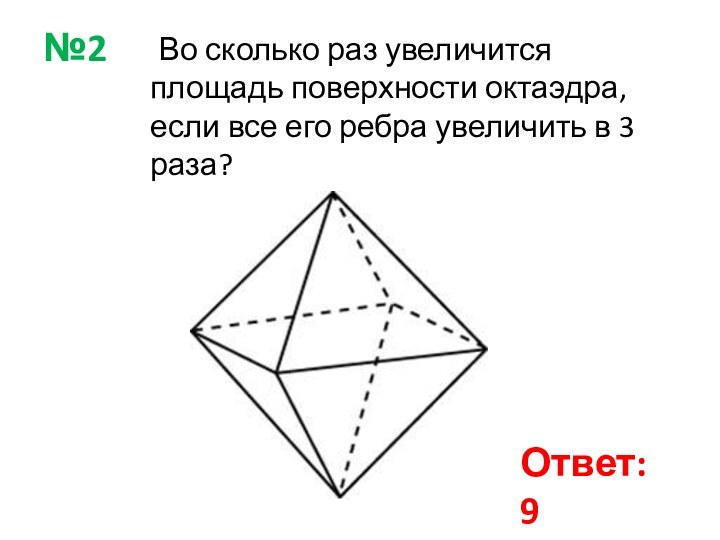
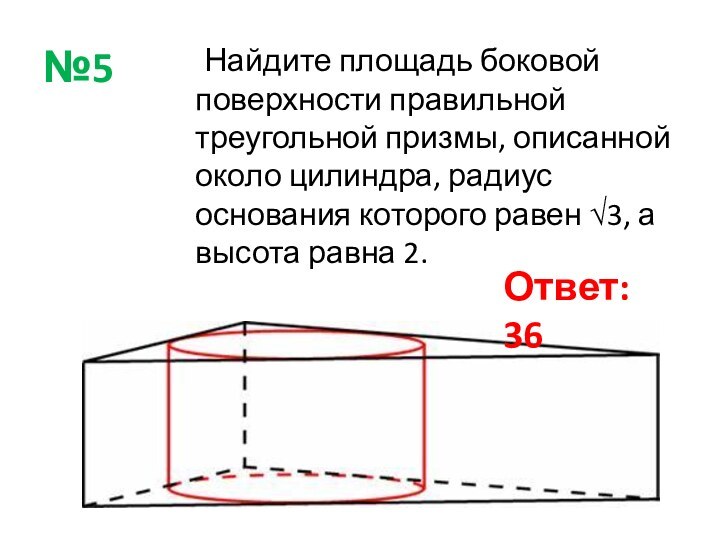
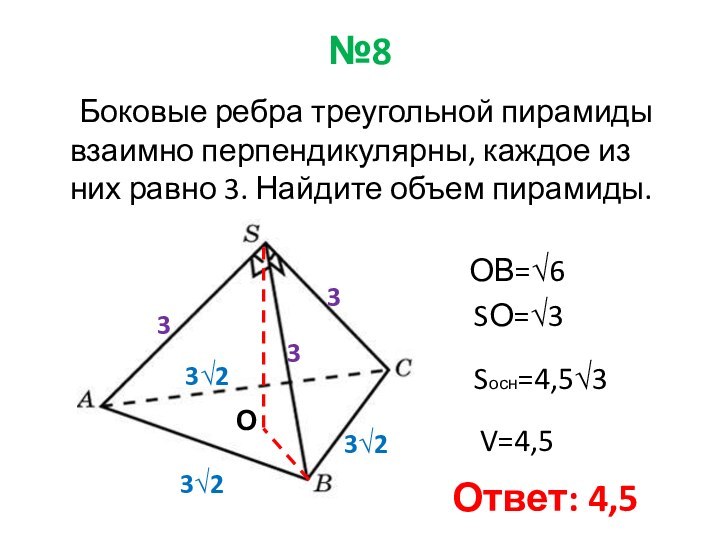
Ответ: 36
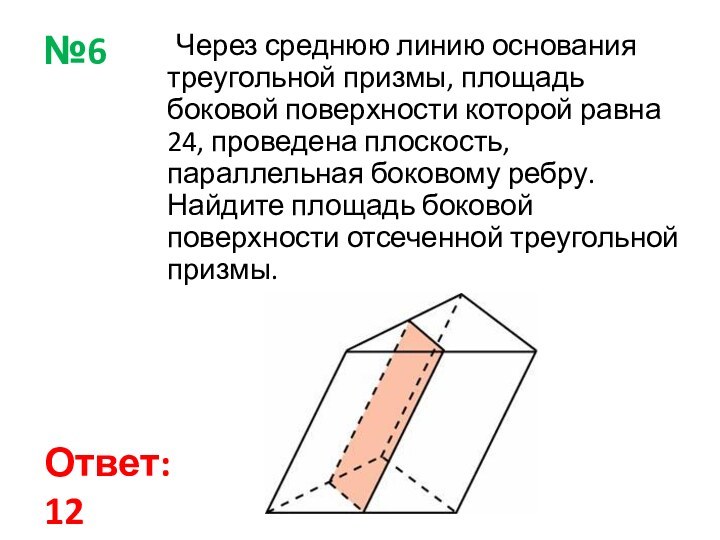
Ответ: 12
30⁰
30⁰
3
3
6
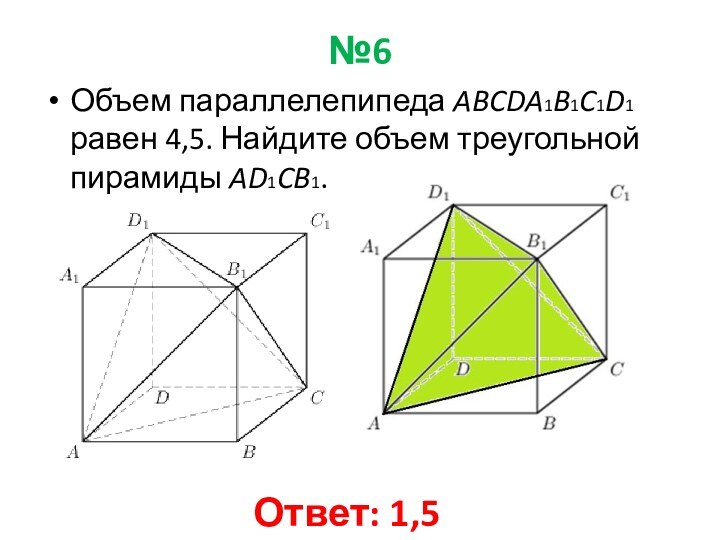
1,5
3
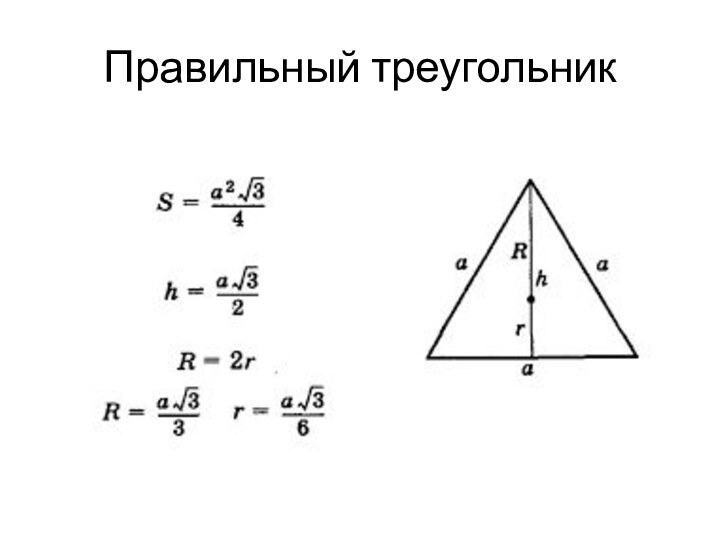
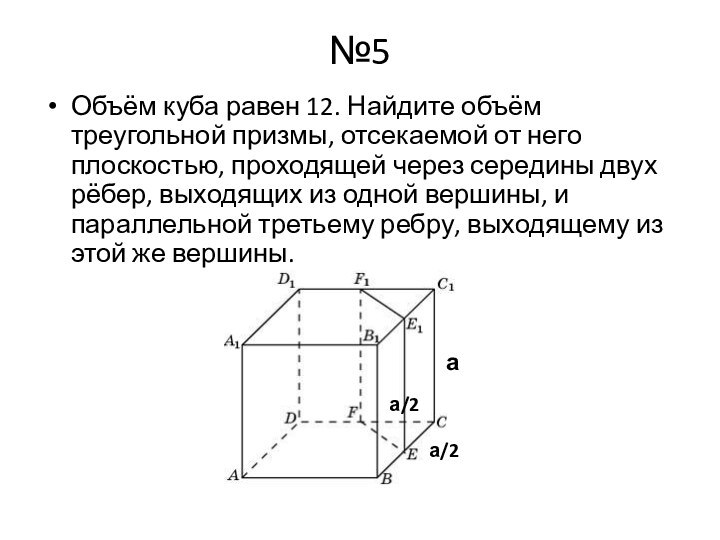
а
а/2
а/2
Ответ: 5
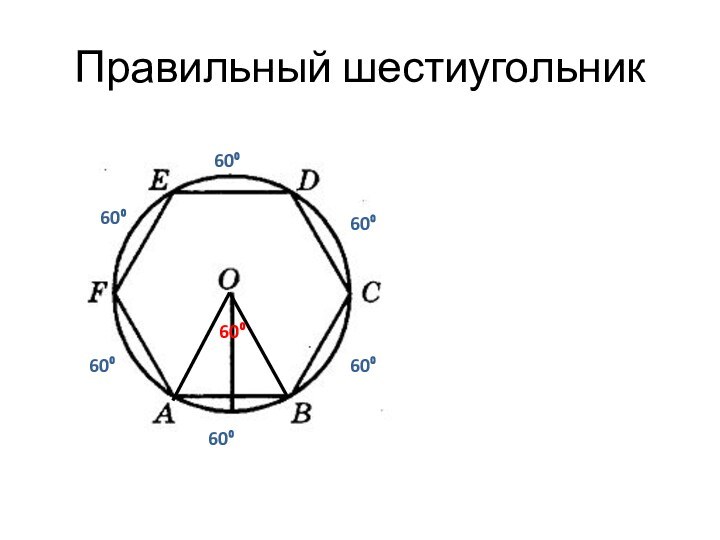
60⁰
60⁰
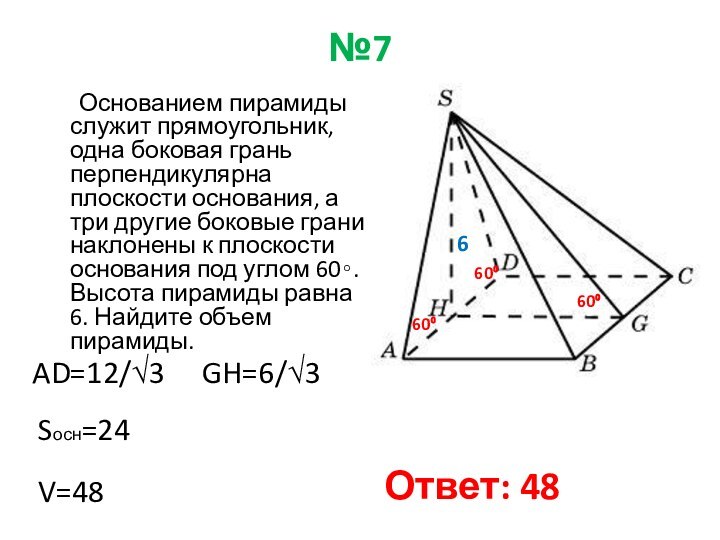
6
AD=12/√3
60⁰
GH=6/√3
Sосн=24
V=48
Ответ: 48
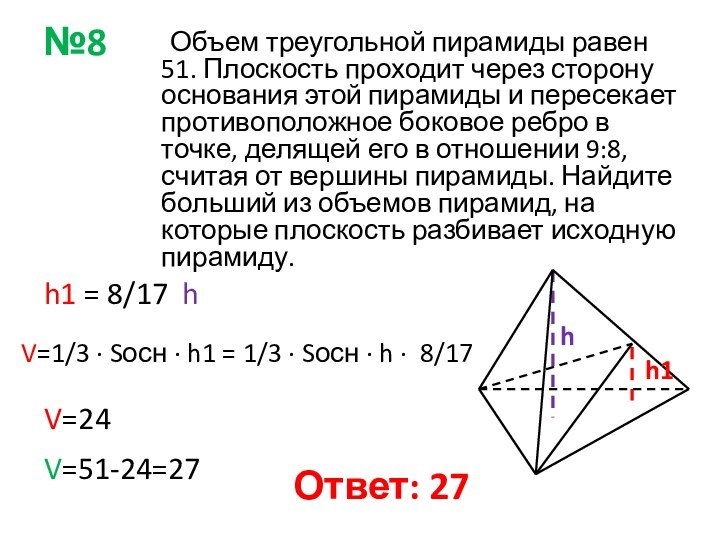
h1 = 8/17 h
V=1/3 ∙ Sосн ∙ h1 = 1/3 ∙ Sосн ∙ h ∙ 8/17
V=51-24=27
V=24
Ответ: 27
h
h1
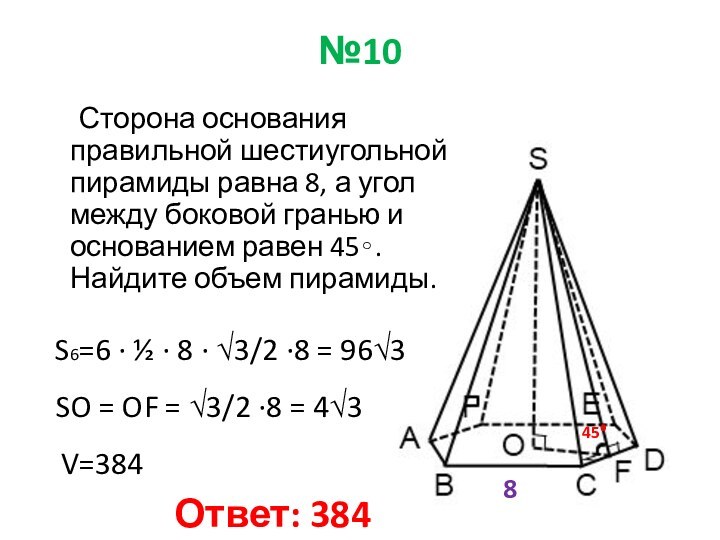
8
45⁰
S6=6 ∙ ½ ∙ 8 ∙ √3/2 ∙8 = 96√3
SO = OF = √3/2 ∙8 = 4√3
V=384
Ответ: 384