Презентация на тему Понятие эконометрики как науки

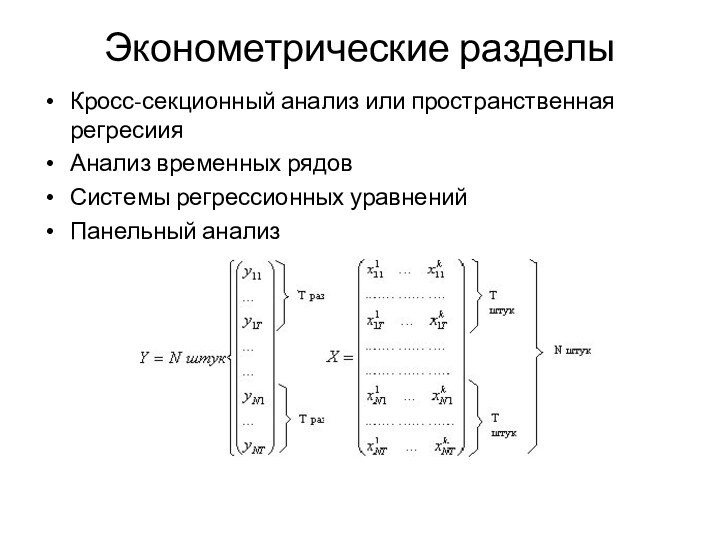
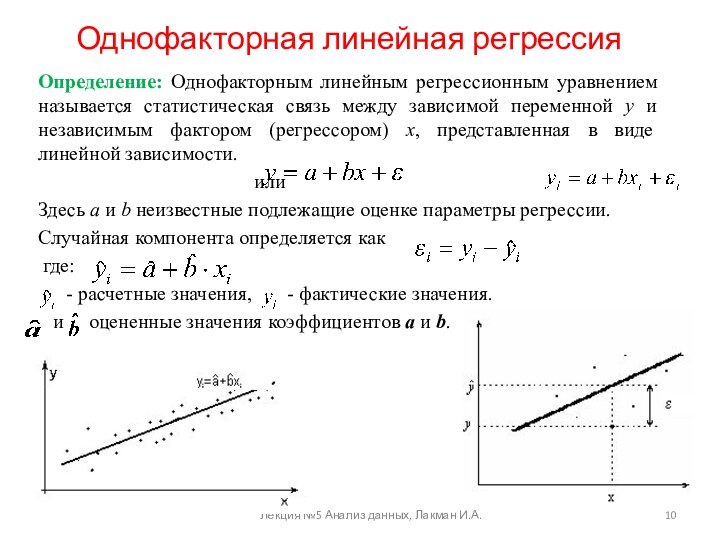
(Анализ или Прогноз, имитационное моделирование)
По иерархии анализируемой информации (макроуровень,

мезоуровень, микроуровень)
По профилю анализируемой экономической системы (теория рисков, инвестиционная политика, анализ спроса и предложения, маркетинговые /геомаркетинговые исследования, налоговая политика, демография, социальная психология, экономическая социология и др.)

регрессионных уравнений
Панельный анализ

(Петти, Кинг)
Конец 19 в. – парная корреляция между брачностью

и благосостоянием в Англии.
1900 г. первые исследования временных рядов (Пирсон, Эрджворт, Гальтон)
1911 исследования по экономической статистике (Р.Мур)
30-ые гг. 20 в. Применение множественной регресии
29.12.1930 И.Фишер, Р.Фриш и Я. Тинберген на заседании Амереканской ассоциации развития науки создали Эконометрическое общество, новая наука –Эконометрика
1933 г. журнал «Эконометрика
1969 первая Нобелевская премия по экономике «досталась» эконометристам Я.Тинбергену, Р. Фришу.

рядов. Модели Бокса и Дженкинса
Производтственые функции –модели экономического роста

Тинберген (Н/П 1969), К. Эрроу (Н/П 1972), Ж.Дебре (Н/П 1972), Р.Солоу (Н/П 1983)
Модели дискретного выбора - Нобелевская премия 2000 г. Хэкман и Макфадден.
Модели условной дисперсии (ARCH-модели) Н/П 2003 (1986) Р. Ингл
Модели коинтеграции временных рядов Н/П 2003 К. Гренджер
Цензурированные модели Н/П 1982 Д.Тобин
2011 г. Н/П Т.Сарджент и К. Симс –макроэконометрические системы регрессионных уравнений.

признака, Х1, Х2,…, Хn, полученные в результате n наблюдений.

Для того чтобы найти статистическую оценку θ неизвестного параметра теоретического распределения через эти данные необходимо найти функцию от наблюдаемых случайных величин, которые дают приближенное значение оцениваемого параметра.
Статистическую оценку, которая определяется одним числом, называют точечной.

Лекция № 5, Анализ данных, Лакман И.А.

свойствами несмещенности, эффективности и состоятельности.
Несмешанной называют статистическую оценку θ*,

математическое ожидание которой равно оценивающему параметру θ при любом объеме выборки, т.е. М(θ*)= θ .
Эффективной оценкой называют статистическую оценку θ*, которая при заданном объеме выборки n имеет наименьшую возможную дисперсию.
Состоятельной называют статистическую оценку, которая при n→ ∞ и стремится по вероятности к оцениваемому параметру, т.е.:
.

Лекция №5, Анализ данных, Лакман И.А.

переменными: между одной зависимой (эндогенной, объясняемой) и одной или

же несколькими независимыми (экзогенными, объясняющими) переменными (факторами, регрессорами). Зависимая переменная обозначается как y, а независимые объясняющие переменные как x1, x2, … , xn.
Различают пространственную регрессию и регрессию временных рядов!!!
Пространственная (spatial) (кросс-секционная,) регрессия проверяет связь между переменными в определенный период времени.
При анализе регрессии во временных рядах (time series) данные по каждой из переменных собираются в течении следующих друг за другом равных периодах времени в одном и том же пространственном субъекте. Регрессионный анализ временных рядов позволяет установить взаимосвязь в среднем в течении того периода времени, по которому имеются данные. Однако за счет возможного влияния показателя времени на временные переменные можно получить ложную регрессию.

Лекция №5,Анализ данных, Лакман И.А.

(условного распределения) одной переменной и соответствующими значениями другой переменной,

называется регрессионным уравнением.
Таким образом, регрессионное уравнение может быть записано в виде
где М(у/х) — условное математическое ожидание случайной переменной у при заданном значении х. В частности, для i-го заданного значения уравнение регрессии записывается в виде.
Регрессионное уравнение есть некая регулярная часть зависимости между у и х, фактически наблюдаемое значение , состоит из этой регулярной части и случайной компоненты :
Наличие случайной компоненты обусловлено двумя причинами:
любая регрессионная модель является упрощением действительности. (на самом деле существуют другие факторы, от которых также зависит переменная Yi);
присутствуют ошибки измерения показателей.

Лекция №5, Анализ данных, Лакман И.А.

статистическая связь между зависимой переменной y и независимым фактором

(регрессором) х, представленная в виде линейной зависимости.
или
Здесь a и b неизвестные подлежащие оценке параметры регрессии.
Случайная компонента определяется как
где:
- расчетные значения, - фактические значения.
и оцененные значения коэффициентов a и b.

Лекция №5 Анализ данных, Лакман И.А.

лежала в

непосредственной близости от фактических наблюдений Yi необходимо минимизировать сумму квадратов отклонений между фактическими и расчетными значениями :

Запишем необходимое условие экстремума:


или


Раскрывая скобки, получим стандартную форму нормальных уравнений:



Разрешая систему относительно

Лекция №5, Анализ данных, Лакман И.А.