Слайд 2
Шкалы измерений (классификация Стивенсона)
Шкала наименований
Шкала порядка
Шкала отношений
Слайд 3
Точность измерений
Абсолютная погрешность измерения (цена деления прибора)
∆А=| А-А0
|, где А – показание измерительного прибора,
А0 -
истинное значение измеряемой величины.
Относительная погрешность измерения
∆А
δА= --------- • 100%
|A|
Слайд 4
Табличное и графическое представление экспериментальных данных
Выборка – ряд
результатов измерений
Объём выборки – количество результатов измерений
Первичная обработка выборки:
а)
данные ранжируются;
б) данные разбиваются на интервалы;
в) составляется вариационный ряд;
г) строятся полигон и гистограмма распределения
Слайд 5
Результаты сдачи ЕГЭ по математике (в баллах), группы
школьников 11 класса (20 человек)
24, 42, 37, 27, 47,
32, 50, 34, 49, 37,
26, 40, 26, 45, 45, 52, 36, 50, 34, 32
а) ранжирование – расстановка результатов измерений в порядке возрастания или убывания
24, 26, 26, 27, 32, 32, 34, 34, 36, 37,
37, 40, 42, 45, 45, 47, 49, 50, 50, 52
Слайд 6
б) разбиение на интервалы
Рекомендуемое число интервалов для выборок
разного объёма
Шаг интервала Xmax
- Xmin
h=
k (Шаг округляется в большую сторону)
h= (52-24):4=7
Слайд 9
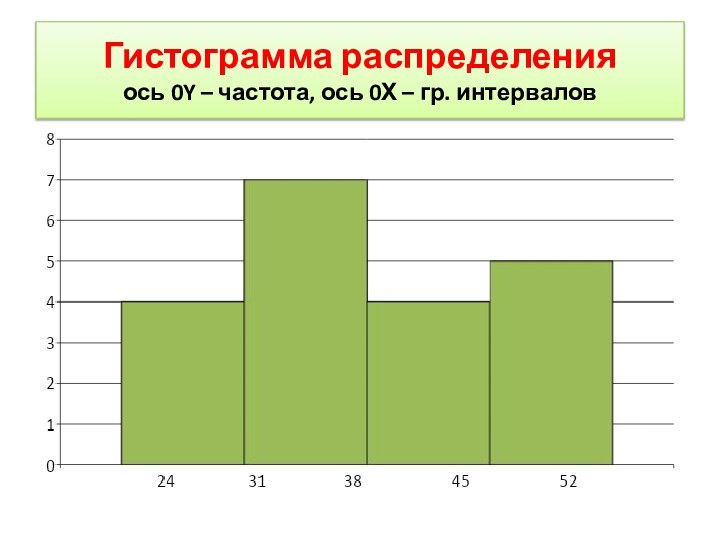
Гистограмма распределения
ось 0Y – частота, ось 0Х –
гр. интервалов
Слайд 10
Характеристики положения
1. Среднее арифметическое значение X для ряда
измерений X1, X2, …,Хn вычисляется по формуле:
n1 •X1 + n2 •X2 + ... + nk •Xk
X = ,
n1 + n2 + ... + nk
где n1, n2, ..., nk - частоты соответствующих интервалов,
X1, Х2, ... Хк - среднее арифметическое значение интервалов.
Слайд 11
Характеристики положения
2. Мода (Мо) – значение в множестве
наблюдений, которое встречается наиболее часто (наиболее представительное значение выборки).
Примеры:
2,
3, 4, 5, 5, 5 Мо = 5
5, 5, 1, 1, 2, 2 Мо - не определяется
1, 2, 2, 2, 3, 3, 3, 4 Мо = 2,5
10,11,11,11,13,14,15,15,15,20 Мо = 11, Мо = 15
Модальный интервал – интервал группировки с наибольшей частотой
Слайд 12
Характеристики положения
Для вычисления моды используется следующая формула:
K-L
Мо = Хнижняя гр.мод.инт.+ h •
(K-L)+(K-P) , где
К - частота модального интервала,
L - частота интервала, ему предшествующего,
Р - частота интервала, следующего за модальным.
Слайд 13
Характеристики положения
Медиана (Ме) – значение в множестве наблюдений,
когда одна половина значений экспериментальных данных меньше её, а
вторая половина – больше.
Примеры:
2, 2, 3, 4, 5, 5, 6 Ме=4
2, 2, 3, 4, 5, 5 Ме=(3+4)/2=3,5
Медианный интервал – интервал, в котором накопленная частота впервые больше N/2 (или накопленная частотность больше 0,5).
N/2 – (накопл.част.инт.,предш.медианному)
Ме=Хн.гр.мед.инт.+ h •
частота медианного интервала
Слайд 14
Характеристики рассеяния
(меры изменчивости)
Колеблемость признака характеризуется величинами: размах
варьирования, дисперсия, среднее квадратическое отклонение и коэффициент вариации.
Размах варирования
R = X max – X min
Дисперсия – средний квадрат отклонения значений признака от среднего арифметического
(X1-X)2 + (Х2-Х)2 + ... + (Хn-Х)2
б2 =
n
(Если n < 30, то в знаменателе дроби – (n-1)).
Слайд 15
Характеристики рассеяния
(меры изменчивости)
Если данные сгруппированы в интервальный
вариационный ряд, то б2 вычисляется по формуле:
n1 (X1-X)2+n2(X2-X)2+. . .+nk(Xk-X)2
б2 =
n
где к - число интервалов, ni - частота i-го интервала,
Xi-серединное значение i-го интервала.
(Если n < 30, то в знаменателе дроби – (n-1)).
Слайд 16
Характеристики рассеяния
(меры изменчивости)
Стандартное отклонение (среднее квадратическое отклонение)
– корень квадратный из дисперсии
б = √ б2
Коэффициент вариации
- отношение среднего квадратического отклонения к среднему арифметическому (выражается в процентах):
б
V = • 100 %
X
Если V≤10% , то выборка считается однородной.
Слайд 17
Нормальный закон распределения результатов эксперимента
Слайд 18
Нормальный закон распределения результатов эксперимента
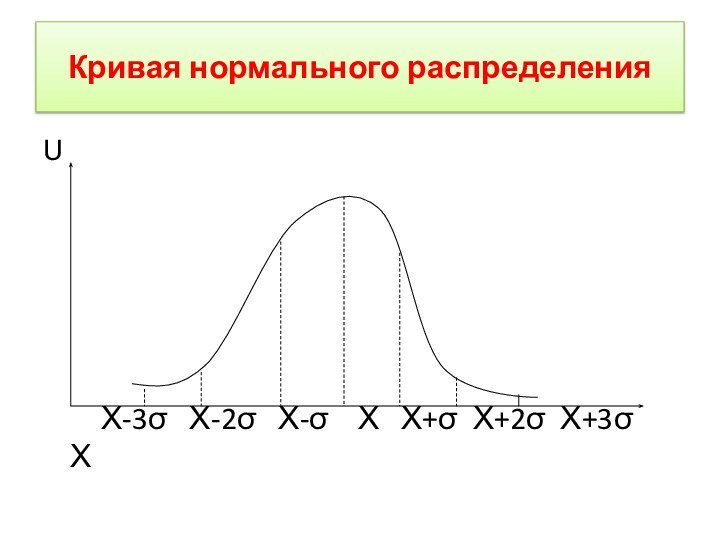
Кривая нормального распределения
– графическая интерпретация формулы нормального распределения, колоколообразная кривая, симметричная
относительно центра группировки (Х).
Для оценки варирования результатов измерений используют соотношения:
Х±σ - включает 68,27% всех результатов;
Х±2σ - включает 95,45% всех результатов;
Х±3σ - включает 99,73% всех результатов
Слайд 19
Кривая нормального распределения
U
Х-3σ
Х-2σ Х-σ Х Х+σ Х+2σ Х+3σ
Х
Слайд 20
Корреляционный анализ
Функциональная зависимость – зависимость, при которой
каждому значению одного показателя строго соответствует определённое значение другого.
Статистическая
взаимосвязь – зависимость, при которой одному значению показателя соответствует несколько значений другого.
Корреляционный анализ – определение связи между двумя случайными величинами и направления этой связи.
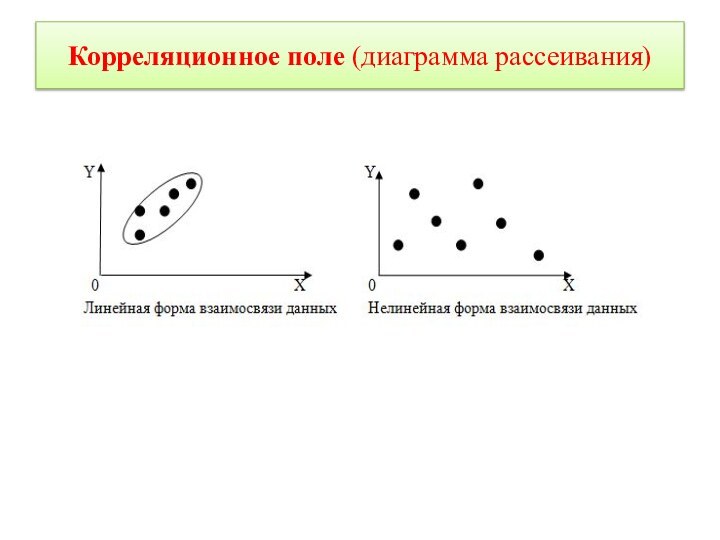
Корреляционное поле (диаграмма рассеивания) - графическое представление измерений в системе координат, когда каждая пара результатов Хi , Yi будет отображаться точкой (Хi ,Yi).
Слайд 21
Корреляционное поле (диаграмма рассеивания)
Слайд 22
Оценка тесноты взаимосвязи
r – коэффициент корреляции (абсолютная величина
тесноты взаимосвязи). 0 ≤ r ≤ 1
Если r
= 1, то взаимосвязь функциональная.
Если 0,7 ≤ r ≤ 0,99 , взаимосвязь сильная статистическая.
Если 0,5 ≤ r ≤ 0,69, то взаимосвязь средняя статистическая.
Если 0,2 ≤ r ≤ 0,49, то слабая статистической связи.
Если 0,09 ≤ r ≤ 0,19, то очень слабая статистическая связь.
Если r=0, то корреляции нет.
Если знак значения r «+», то связь положительная, если знак «-», то связь отрицательная.
Слайд 23
Корреляционное поле
(некоторых значений коэффициента корреляции)
Слайд 24
Парный коэффициент корреляции Браве-Пирсона
Слайд 25
Парный коэффициент корреляции Браве-Пирсона
Пример: экспериментальные данные представляют собой
результаты в запоминании основных формул характеристики рассеяния (меры изменчивости)
(в мин.), показанные группой студентов (20 человек).
Эти же студенты участвовали в соревнованиях по прыжкам в высоту. Данные этих испытаний представлены в таблице:
Данные для расчёта: n=20, Xср.=16,7; Yср.=97,7; σх = 0,637 и σу = 8,03
r = 0,391
Слайд 26
Коэффициент корреляции Спирмена
Слайд 27
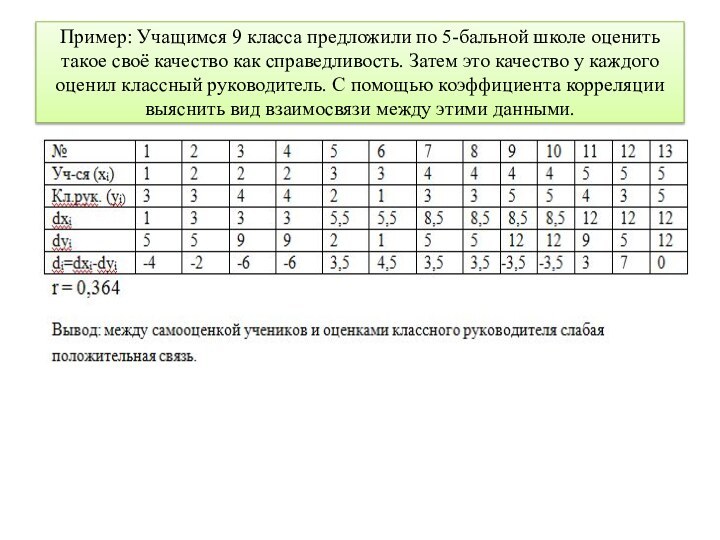
Пример: Учащимся 9 класса предложили по 5-бальной школе
оценить такое своё качество как справедливость. Затем это качество
у каждого оценил классный руководитель. С помощью коэффициента корреляции выяснить вид взаимосвязи между этими данными.
Слайд 28
Тетрахорический коэффициент корреляции Пирсона rA
Пример: Группа испытуемых
решала две математические задачи: одну по теории вероятностей, другую
по математической статистике. Задачу по математической статистике верно решили испытуемые, записаны в списке под номерами: 1, 2, 4, 5, 7, 8, 9, 10. А задачу по математической статистике: 2, 3, 4, 9, 10. Определить степень эквивалентности этих значений.
Слайд 29
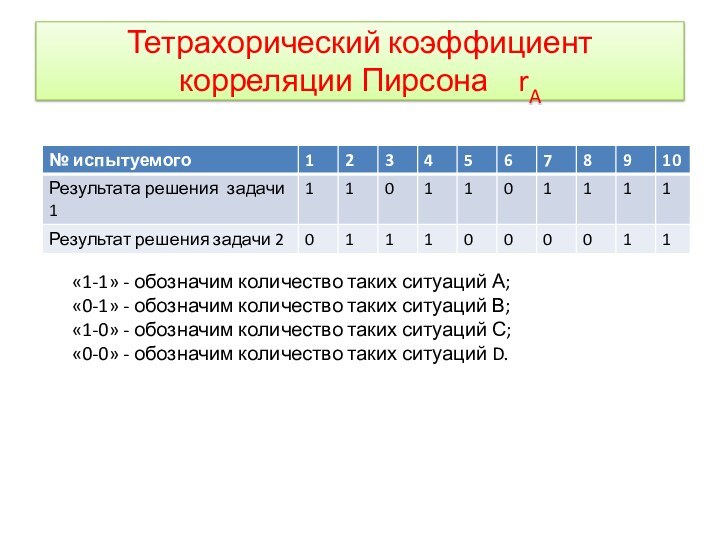
Тетрахорический коэффициент корреляции Пирсона rA
«1-1» - обозначим
количество таких ситуаций А;
«0-1» - обозначим количество таких ситуаций
В;
«1-0» - обозначим количество таких ситуаций С;
«0-0» - обозначим количество таких ситуаций D.
Слайд 30
Тетрахорический коэффициент корреляции Пирсона rA
Слайд 31
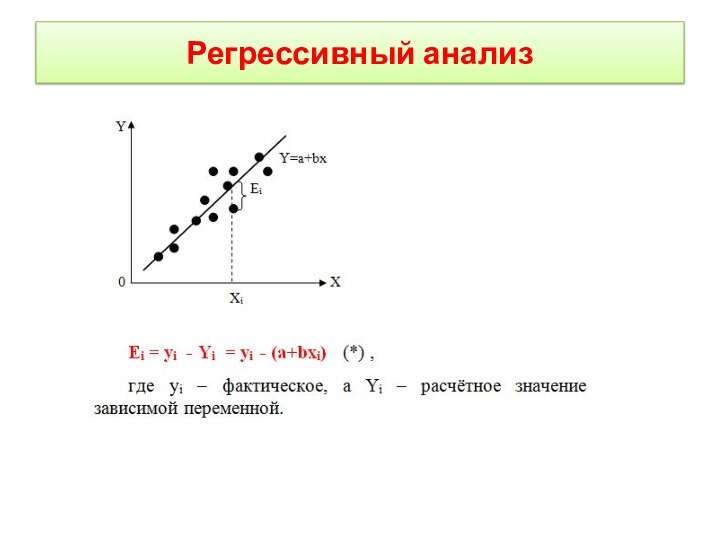
Регрессивный анализ
это установление зависимости между случайной величиной Y
и значением одной или нескольких переменных величин. Зависимость описывается
уравнением регрессии.
Y = а ∙ Х + b
a - ? b - ?
Слайд 34
Пример. В таблице приведены результаты, показанные группой школьников
(10 человек) в беге на дистанции 30м (хi,) и
100м (yi) в секундах.