Презентация на тему по статистике.Методы распределения.

характеристики, в частности, определяются мо­менты распределения.
Моментом k-го порядка называется средняя

из k-x степеней от­клонений вариантов х от некоторой постоянной величины А:

частостей моменты называются эмпирически­ми, а при использовании вероятностей — теоретическими.
Эмпирический мо­мент k-го порядка:

= О):

не нулю, а некоторой производной величине Х0 (начало отсчета):

ряда распределения. При подстановке различных зна­чений k получаем начальные моменты относительно Хо. Так,

напри­мер, если k = 1, то:                                       

равна началу отсчета плюс начальный момент первого поряд­ка. Если

отклонения (хi- х0) имеют общий множитель С, то на него можно разделить отклонения, а по окончании вычислить полученный момент, умножив на этот множитель в соответствующей степени, т.е.:




Отсюда следует, что при k = 1 x=x0+m1*C.

арифметическую (А=х):

закономерность, выражением которой является кривая распределения, представляющая собой функцию распределения.

Можно выделить определенную зависимость между изменением частот и изменением значений признаков: частоты изменяются закономерно с изменением варьирующего признака, т. е. с увеличением значения варьирующего признака частоты первоначально увеличиваются, затем, достигнув  какой-то максимальной величины в середине ряда, уменьшаются. Такие закономерности изменения частот в вариационных рядах называются закономерностями распределения. Эмпирическим распределением называют распределение частот (относительных частот), соответствующих отдельным значениям признака, функционально связанных с изменением вариант.

не частоты (f), а вероятности (p), то получим теоретические

моменты распределения. Отсюда –теоретическим называют распределение вероятностей. Если имеется эмпирический ряд распределения, то необходимо найти функцию распределения, т. е. подобрать такую теоретическую кривую распределения, которая бы наиболее полно отражала закономерность распределения. Под кривой распределения понимается графическое изображение в виде непрерывной линии изменения частот (вероятностей), функционально связанных с изменением вариант. Закон распределения случайной величины может быть задан в виде таблицы, функции распределения либо плотности распределения.

теоретических распределений: распределение Стьюдента, Пуассона, нормальное распределение, хи-квадрат распределение,

распределение Фишера, биномиальное (распределение Бернулли), равномерное распределение. Каждое из теоретических распределений имеет специфику и свою область применения в различных отраслях знаний. Первым фундаментальным по значимости является нормальный закон распределения (ЗНР).

действует вместе. Часто возникают распределения, хотя и не отвечающие

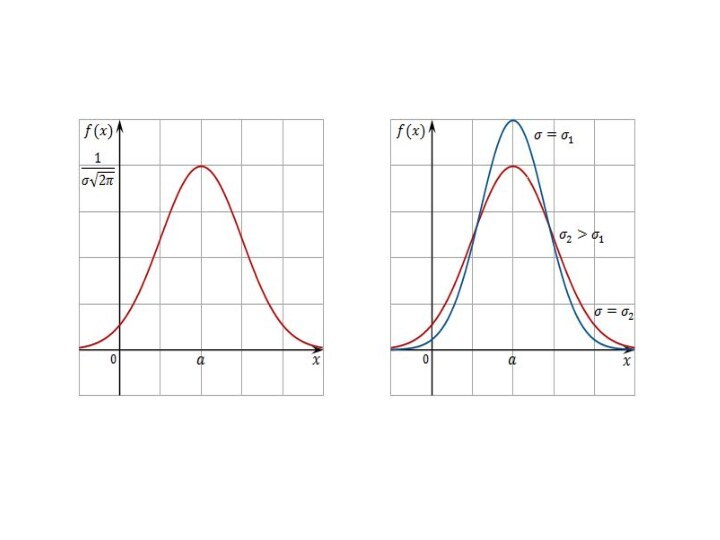
строго нормальному распределению, но имеющие с ним сходство, а именно: вероятность min и max значений тем меньше, чем больше отклонение отдельных вариант от общей средней. Иными словами: минимальные и максимальные варианты встречаются много реже, чем серединные. Нормальное распределение полностью определяется двумя входными параметрами: средней арифметической и среднеквадратическим отклонением (Ϭ).

учесть величину среднеквадратического отклонения Ϭ, то окажется, что при

больших значениях Ϭ значение плотности вероятности f(x) мало и наоборот – при малых значениях Ϭ плотность вероятности (ордината точки максимума) неограниченно возрастает. Отсюда: среднеквадратическое отклонение нормально распределенной СВ существенно влияет на форму нормальной кривой. Максимальная ордината кривой обратно пропорциональна среднеквадратическому отклонению Ϭ. Вся площадь, ограниченная кривой распределения и осью абсцисс, равна 1.

константы:  

 
Это распределение характерно тем, что в соответствующих пределах заключено

соответствующее количество всех частот:   

единице (0,9973), случайная величина, подчиняющаяся закону нормального  распределения, не выйдет

за пределы заданного интервала. Это утверждение называют правилом трёх сигм. Вероятность того, что СВ примет значение за пределами заданного интервала, крайне мала: (1- 0,9973=0,0027)   

предполагает оценку его однородности, а также расчет показателей асимметрии

и эксцесса.
При сравнительном изучении асимметрии нескольких распределений с разными единицами измерениявычисляется относительный показатель асимметрии:



Его величина может быть положительной (для правосторонней асимметрии) и отрицательной (для левосторонней асимметрии).

только величину асимметрии, но и проверить ее наличие в генеральной

совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной. Если асимметрия меньше 0,25, она считается незначительной.
Наличие асимметрии в генеральной совокупности проверяется с помощью определения оценки существенности на основе средней квадратической ошибки:

, асимметрия считается

существенной
и
распределение признака в генеральной совокупности несимметрично и неслучайно, а закономерно.
Для симметричных распределений может быть рассчитан показатель эксцесса, который показывает, насколько резкий скачок имеет изучаемое явление. Показатель эксцесса определяется на основе центрального момента четвертого порядка по формуле:

распределение островершинное и скачок считается значительным, если коэффициент эксцесса

меньше нуля, то распределение считается плосковершинным и скачок считается незначительным. Среднеквадратическая ошибка эксцесса показывает, насколько существенен скачок в явлении и рассчитывается по формуле: