- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Production management
Содержание
- 2. EOQ ModelEconomic Order Quantity is the order
- 3. OverviewEconomic order quantity is the order quantity
- 4. Underlying assumptions The ordering cost is constant. The rate
- 5. Variablesc : purchase price, unit production costQ
- 6. The total cost functionTo obtain the optimal value of Q*, we compute…
- 7. Optimal value of QAt optimal value of
- 8. Price of the item based on the
- 9. Order cost dependent of quantityIt is often
- 10. Degressive prices based on quantityIt is often
- 11. Periodic replenishment The idea is to replenish
- 12. Model based on the service rateThe criterion
- 13. Stock with zero rotation: the newsagentExample 1We
- 14. Stock with zero rotation: the newsagentModelLet px
- 15. Stock with zero rotation: the newsagentWith the
- 16. Stock with zero rotation: the newsagentExerciseThe newsagent
- 17. Replenishment with CP, CR based on time
- 18. Since T is a given, the overall
- 19. With the cumulative probability function F(S), the
- 20. L(S) is a positive function, So, we
- 21. ExerciseA workpiece is supplied every 15 days.
- 22. ExerciseS* = 23 unitésReplenishment with CP, CR
- 23. Replenishment with CR based on number of
- 24. H(S) is a positive functionIfIfReplenishment with CR
- 25. ExerciseA shop sells every week between 20
- 26. Скачать презентацию
- 27. Похожие презентации























Слайд 3
Overview
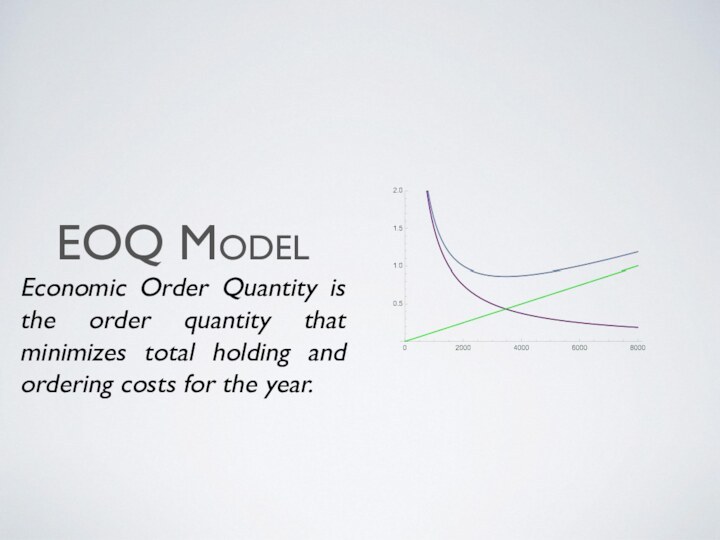
Economic order quantity is the order quantity that
minimizes total inventory holding costs and ordering costs. It
is one of the oldest classical production scheduling models.EOQ applies only when demand for a product is constant over the year and each new order is delivered in full when inventory reaches zero. There is a fixed cost for each order placed, regardless of the number of units ordered. There is also a cost for each unit held in storage, commonly known as holding cost, sometimes expressed as a percentage of the purchase cost of the item.
EOQ search to determine the optimal number of units to order to minimize the total cost associated with the purchase, delivery and storage of the product.
The required parameters to the solution are the total demand for the year, the purchase cost for each item, the fixed cost to place the order and the storage cost for each item per year. Note that the number of times an order is placed will also affect the total cost, though this number can be determined from the other parameters.
Слайд 4
Underlying assumptions
The ordering cost is constant.
The rate of
demand is known, and spread evenly throughout the year.
The
lead time is fixed.The purchase price of the item is constant i.e. no discount is available
The replenishment is made instantaneously, the whole batch is delivered at once.
Only one product is involved.
Слайд 5
Variables
c : purchase price, unit production cost
Q :
order quantity
Q* : optimal order quantity
D : annual demand
quantityK : fixed cost per order, setup cost (not per unit, typically cost of ordering and shipping and handling. This is not the cost of goods)
H : annual holding cost per unit, also known as carrying cost or storage cost (capital cost, warehouse space, refrigeration, insurance, etc. usually not related to the unit production cost)
Слайд 7
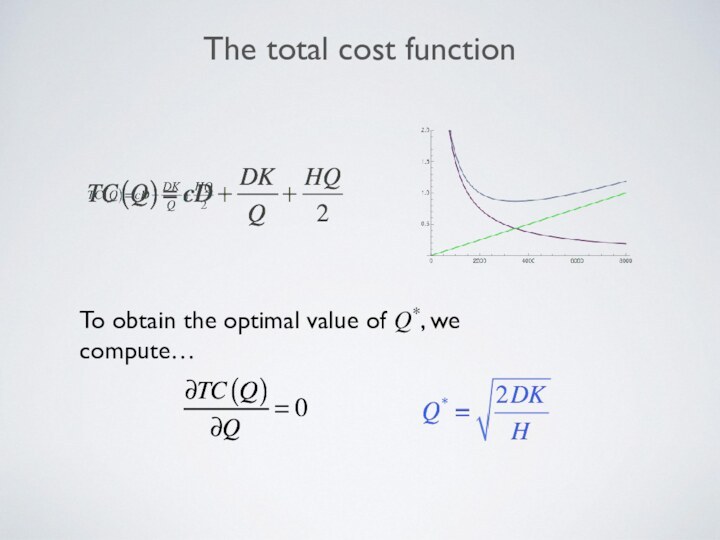
Optimal value of Q
At optimal value of Q*,
we have the same holding cost and order cost…
Q*
C(Q*)
Слайд 8 Price of the item based on the quantity
ordered
It is often possible to obtain price discounts when
quantities ordered are below certain thresholds10 € per item when the order quantity is in interval ]0 ; 400[.
9,5 € per item when the order quantity is in interval [400 ; 600[.
9 € per item when the order quantity is in interval [600 ; inf[.
Formally, order are partitioned to intervals [ai, bi] based on the price of the item
Algorithm
Compute Q*
For each interval :
Determine Qopt
Compute R(Qopt)
Keep Qopt giving min(R(Qopt))
Слайд 9
Order cost dependent of quantity
It is often possible
to obtain price discounts when quantities ordered are below
certain thresholdsK = 1000 €, if Q ≤ 400 (road transport)
For each intervals [ai, bi], order cost is different…
Algorithm
For each interval :
Compute Q* based on K
Determine Qopt
Compute C(Qopt)
Keep Qopt giving min(C(Qopt))
K = 1500 €, if Q > 400 (rail transport)
D =1000 item / day
H =1 € / item / day
?
?
?
?
?
?
Слайд 10
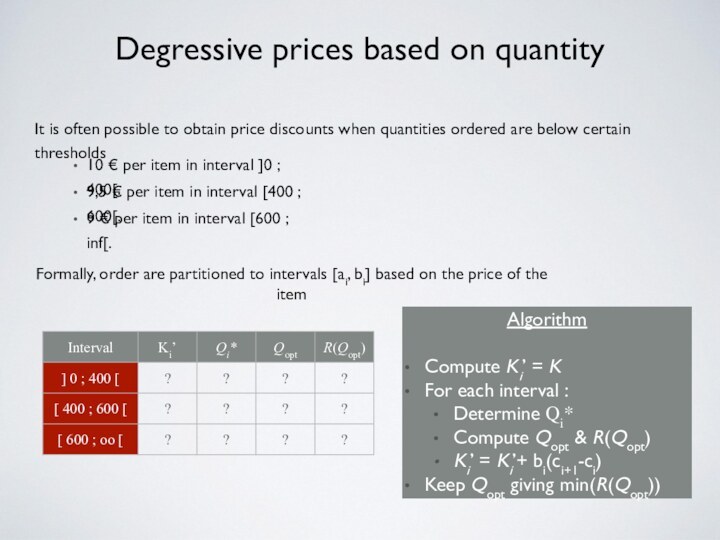
Degressive prices based on quantity
It is often possible
to obtain price discounts when quantities ordered are below
certain thresholds10 € per item in interval ]0 ; 400[.
9,5 € per item in interval [400 ; 600[.
9 € per item in interval [600 ; inf[.
Formally, order are partitioned to intervals [ai, bi] based on the price of the item
Algorithm
Compute Ki’ = K
For each interval :
Determine Qi*
Compute Qopt & R(Qopt)
Ki’ = Ki’+ bi(ci+1-ci)
Keep Qopt giving min(R(Qopt))
Слайд 11
Periodic replenishment
The idea is to replenish the
stock level up to the maximum quantity at fixed
period
Слайд 12
Model based on the service rate
The criterion is
to supply the demand. There are two indicators:
α: Probability
to meet demand without breakingβ: Ratio between the number of items supplied and demand
Exemple
A pharmacist sells every day 6-9 boxes of some infant vaccine. The vaccine should be kept refrigerated. Space is limited and replenishment is daily. The pharmacist decides to fix the reorder point 7 boxes.
Слайд 13
Stock with zero rotation: the newsagent
Example 1
We consider
that the cost of holding CP is equal to
the cost of unsold for an article.The cost of shortage CR is proportional to the number of missing items.
A newsagent buys every day a fixed amount of a magazine. It pays each copy 2 € and sold 3 €, representing a margin of 1 €.
If demand exceeds its stock, it finds a shortfall of 1 €, so CR = 1. Any unsold magazine was bought 1.5 € per press group which causes a loss of 0.5 €, so CP = 0,5.
Слайд 14
Stock with zero rotation: the newsagent
Model
Let px the
probability that the demand X is equal to x
items on period T and S is the desired level of stock.if x ≤ S there is (S-x) unsold, representing a cost of CP(S-x)
Si x > S, (x-S) items are missing, representing a cost of CR(x-S)
A request of x articles having a probability px of occurring, the average total cost is given by:
Warning : it is for x ≤ S and x > S. If we have x < S et x ≥ S, we obtain:
Eq. 1
Eq. 2
Слайд 15
Stock with zero rotation: the newsagent
With the cumulative
density function F(S), we obtain
Let
S* is the only optimal
solution(S*-1) and S* are the two optimal solutions
If
If
Слайд 16
Stock with zero rotation: the newsagent
Exercise
The newsagent observed
over 10 weeks the number of newspapers sold.
Every
day, he sold between 20 and 60 magazinesWhat is the optimal level of inventory?
CP = 3
CR = 2
Слайд 17 Replenishment with CP, CR based on time and
number of articles
Model
1. If x ≤ S, there is
no out of stockBy approximating the demand with a line, we obtain:
Let CP and CR holding cost and shortage cost for one item for a period.
Let x the observed demand during the period T.
1. if x ≥ S, after a time T1, there is out of short
Holding costs amounted to
Shortage costs amounted to
Thanks to Chasles relation a :
Given a total cost
Слайд 18 Since T is a given, the overall cost
will be used per unit of time:
With probability….
And, if
we consider instead x < S et x ≥S, we obtain:Replenishment with CP, CR based on time and number of articles
Слайд 19 With the cumulative probability function F(S), the relation
can be expressed by:
Let
Replenishment with CP, CR based on
time and number of articlesСлайд 20 L(S) is a positive function, So, we obtain
a similar result to the previous problem...
Moreover, L(S) is
strictly increasing, so:If
If
S* is the only optimal solution
(S*-1) and S* are the two optimal solutions
Replenishment with CP, CR based on time and number of articles
Слайд 21
Exercise
A workpiece is supplied every 15 days. It
is estimated that the shortage cost for a period
is equivalent to 20 holding cost (over the same period).Over 15 days, the demand varie from 20 to 27.
Replenishment with CP, CR based on time and number of articles
Слайд 22
Exercise
S* = 23 unités
Replenishment with CP, CR based
on time and number of articles
A workpiece is supplied
every 15 days. It is estimated that the shortage cost for a period is equivalent to 20 holding cost (over the same period).Over 15 days, the demand varie from 20 to 27.
Слайд 23
Replenishment with CR based on number of articles
Model
This
model differs from the previous by the computation of
the shortage costWhen x ≥ S, after a period T1, ther is out of stock
Shortage cost:
In terms of probability, total cost will be:
Let
Слайд 24
H(S) is a positive function
If
If
Replenishment with CR based
on number of articles
S* is the only optimal solution
(S*-1)
and S* are the two optimal solutions
Слайд 25
Exercise
A shop sells every week between 20 and
25 computers. Replenishment is done every Thursday night. With
competition strong, anyone who can not take his product will buy directly from a competitor. In this case, the distributor estimates its loss to 200 €. On the other hand, the shop buys a computer 2000 € and estimates the annual holding cost to 25% of the purchase price.Replenishment with CR based on number of articles