- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Производственные функции
Содержание
- 2. Определение производственной функцииОпределение. Производственная функция n независимых
- 3. Производственную функцию называют многоресурсный, или многофакторный. Пример.
- 4. Типы производственных функцийОпределение 1. Производственная функция называется
- 5. Основные свойства производственной функцииПри отсутствии одного из
- 6. При неограниченном увеличении одного из ресурсов
- 7. Свойства функции Кобба-ДугласаПри 2. Первые частные производные положительные:Функция Кобба - Дугласа возрастающая.
- 8. 3. Вторые частные производные отрицательные:
- 9. С ростом ресурсов скорость роста выпуска замедляется.4. При
- 10. Вывод. Показатель
- 11. При
- 12. Производственная функция характеризуется следующими понятиями:
- 13. Изокванты. Изоклинали. Изоквантой называется линия уровня в системе
- 14. LЭта степенная гипербола,
- 15. Так какдифференциалы
- 16. Аналогично определяется предельная норма замены капитала трудом
- 17. Определение. Изоклиналью называется линия наибольшего роста производственной
- 18. При прохождении изоклинали через точку с координатами
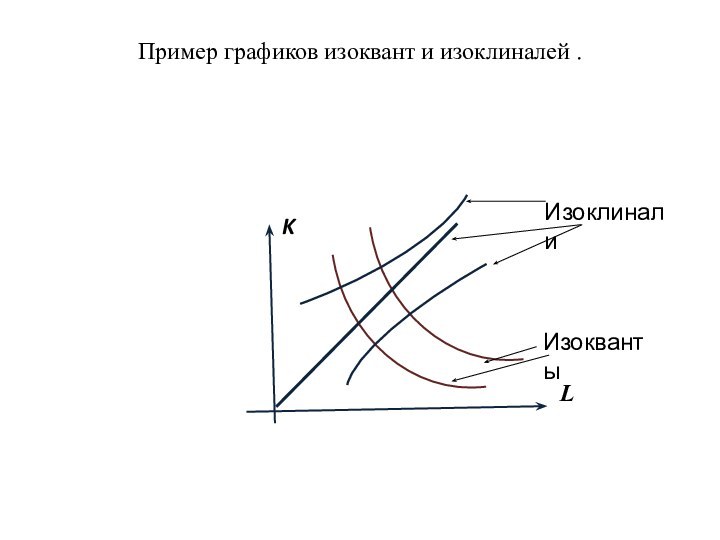
- 19. Пример графиков изоквант и изоклиналей .LИзоклиналиИзокванты
- 20. З а д а ч а .
- 21. Р е ш е н и е.
- 22. Запишем функцию Кобба –Дугласа через приращения:где
- 23. Получим коэффициенты эластичности:
- 24. 2) Средняя производительность труда:Предельная производительность труда:3) Средняя
- 25. Если стоимость основных фондов увеличить в 100
- 26. Скачать презентацию
- 27. Похожие презентации
Определение производственной функцииОпределение. Производственная функция n независимых переменных – это функция, независимые переменные которой принимают значения объемов затрачиваемых или используемых ресурсов, а зависимая переменная – значения объемов выпускаемой продукции.





















Слайд 2
Определение производственной функции
Определение. Производственная функция n независимых переменных
Слайд 3
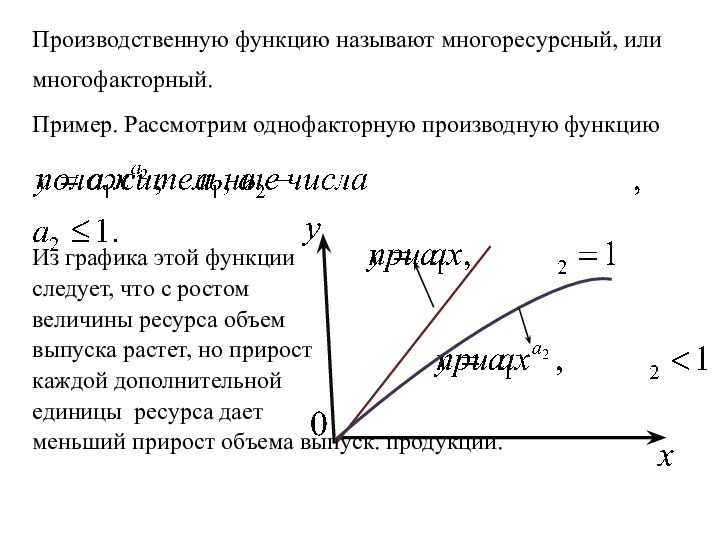
Производственную функцию называют многоресурсный, или многофакторный.
Пример. Рассмотрим
однофакторную производную функцию
Из графика этой функции
следует, что с ростом
величины ресурса объем
выпуска растет, но прирост
каждой дополнительной
единицы ресурса дает
меньший прирост объема выпуск. продукции.
Слайд 4
Типы производственных функций
Определение 1. Производственная функция называется статической,
если ее переменные относятся к определенному моменту времени или
природу времени, без учета временных изменений этих параметров.Определение 2. Производственная функция называется динамической, если ее переменные зависят от времени, а также взаимосвязаны во времени.
Слайд 5
Основные свойства производственной функции
При отсутствии одного из ресурсов
производство невозможно:
С ростом ресурсов выпуск растет:
С ростом ресурсов
скорость роста выпуска замедляется:Слайд 6 При неограниченном увеличении одного из ресурсов выпуск
неограниченно растет:
Для решения и анализа задач экономики часто
используют мультипликативную производственную функцию вида:Частным случаем мультипликативной производственной функции является функция Кобба-Дугласа, у которой
Функцию Кобба-Дугласа представляется
Слайд 7
Свойства функции Кобба-Дугласа
При
2. Первые частные
производные положительные:
Функция Кобба - Дугласа возрастающая.
Слайд 9
С ростом ресурсов скорость роста выпуска замедляется.
4. При неограниченном
увеличении одного из ресурсов выпуск неограниченно растет:
Функция Кобба –
Дугласа не имеет экстремумов.Линии уровня производственной функции Кобба – Дугласа гиперболы.
Найдем эластичности мультипликативной производственной функции. Эластичность выпуска по основным фондам определяется формулами:
Слайд 10
Вывод.
Показатель является
эластичностью выпуска по основным фондам.
Аналогично доказывается, что эластичность
выпуска по труду равна .Для мультипликативной производственной функции
показатель степени является эластичностью выпуска по основным фондам, а эластичность выпуска по труду равна .
При имеет место трудосберегающий (интенсивный) рост, а при -фондосберегающий (экстенсивный).
Слайд 11 При
мультипликативная производственная функция
описывает растующую экономику. Действительно, темп роста выпуска определяется соотношениемВозведем обе части выражения в степень .
Получим
Слайд 13
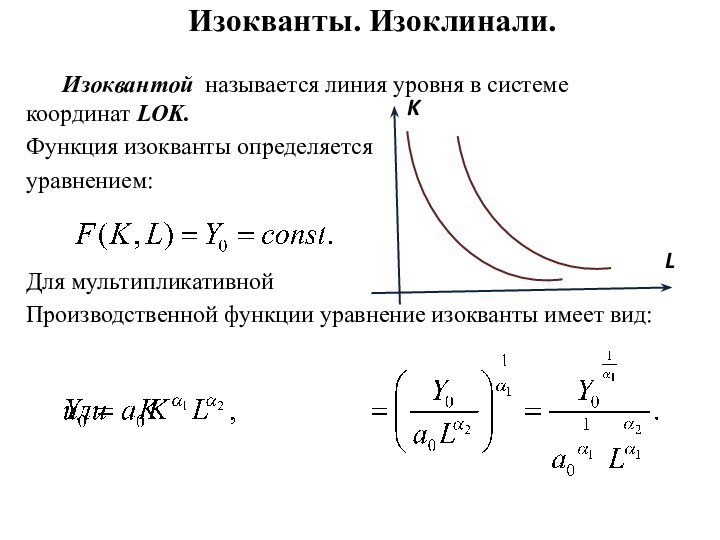
Изокванты. Изоклинали.
Изоквантой называется линия уровня в системе координат
LOK.
Функция изокванты определяется
уравнением:
Для мультипликативной
Производственной функции уравнение
изокванты имеет вид: L
Слайд 14
L
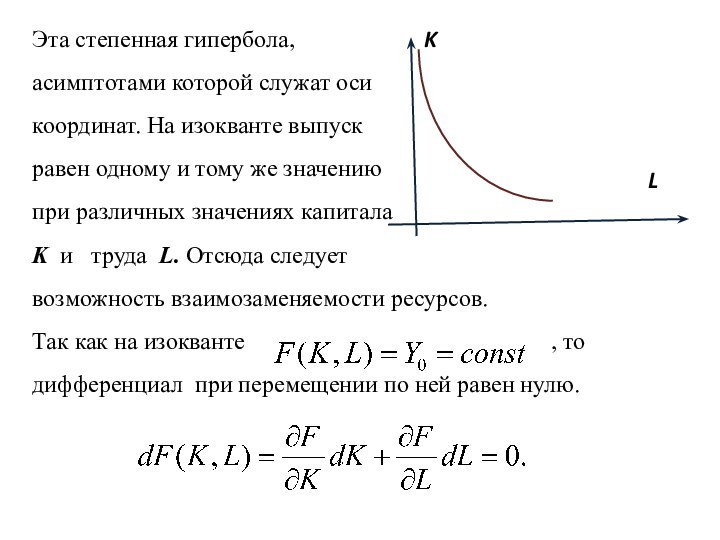
Эта степенная гипербола,
асимптотами
которой служат оси
координат. На изокванте выпуск
равен одному и тому
же значениюпри различных значениях капитала
K и труда L. Отсюда следует
возможность взаимозаменяемости ресурсов.
Так как на изокванте , то дифференциал при перемещении по ней равен нулю.
Слайд 15
Так как
дифференциалы
имеют
разные знаки.Определение. Предельной нормой замены труда капиталом (фондами) называется отношение модулей дифференциалов капитала и труда:
Слайд 16 Аналогично определяется предельная норма замены капитала трудом
:
Их двух формул видно, что
Для
мультипликативной производственной функции имеем
Слайд 17
Определение. Изоклиналью называется линия наибольшего роста производственной функции.
Изоклинали
ортогональны изаквантам. Уравнение изоклинали имеет вид:
Для мультипликативной
производственной функции имеемРешение этого дифференциального уравнения имеет вид:
С- произвольная постоянная.
Слайд 18
При прохождении изоклинали через точку с координатами
постоянная
интегрирования определяется формулой:Подставляя полученное значение в выражение ,
получим сл.
Изоклиналь, проходящая через начало координат, определяется формулой: т.е. является прямой линией.
Слайд 20 З а д а ч а . Пусть
некоторое производство можно описать с помощью функции Кобба –
Дугласа. В настоящее время один работник производит в месяц продукции на 1 млн. руб. Общая численность работников 1000 человек. Основные фонды оцениваются в 10 млрд.руб. Известно, что для увеличения выпуска продукции на 3 % следует увеличить или стоимость фондов на 6 %, или численность работников на 9%.Составить для данного предприятия производственную функцию, определив коэффициенты эластичности.
Определить среднюю и предельную производительность труда.
Определить среднюю и предельную фондоотдачу.
Найти нормы замещения ресурсов, предельные нормы замещения ресурсов.
Определить численность работников, если стоимость основных фондов увеличить в 100 раз, уменьшить в 100 раз.
Слайд 21
Р е ш е н и е.
1.
Производственная функция Кобба –Дугласа имеет вид:
,где - затраченный труд, - капитал. Найдем коэффициенты эластичности. По условию имеем человек, руб.
Тогда объем продукции в стоимостном соотношении можно определить как произведение общая численность работников на производительность одного работника в месяц:
руб.
Слайд 22
Запишем функцию Кобба –Дугласа через приращения:
где
- прирост объема продукции;
- прирост трудовых ресурсов;
- прирост фондов.
По условию известно, что для увеличения выпуска продукции на 3 % (т.е. ) следует увеличить стоимость фондов на 6 % (т.е.
или численность работников увеличить на 9 %
(т.е. ). Имеем следующую систему:
Слайд 23
Получим коэффициенты эластичности:
.
Тогда производственная функция
имеетвид: ,
Итак, производственная функция имеет вид:
Слайд 24
2) Средняя производительность труда:
Предельная производительность труда:
3) Средняя фондоотдача:
Предельная фондоотдача:
4) Норма замещения первого ресурса
вторым:Норма замещения второго ресурса первым:
Предельная норма замещения второго ресурса первым:
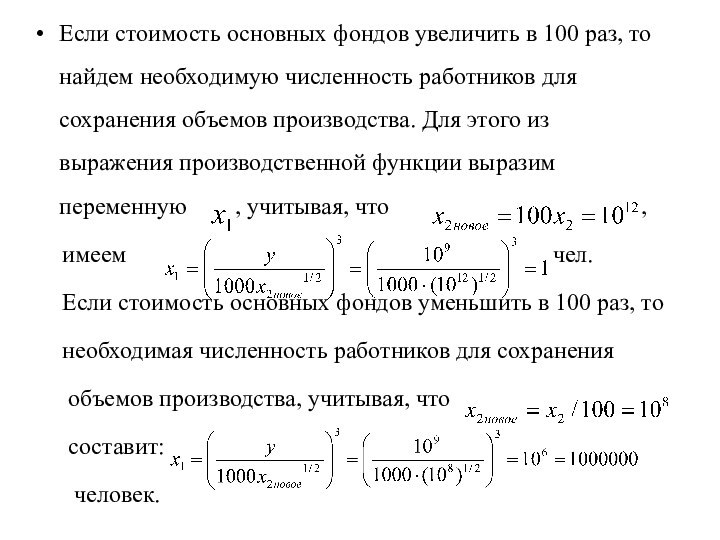
Слайд 25 Если стоимость основных фондов увеличить в 100 раз,
то найдем необходимую численность работников для сохранения объемов производства.
Для этого из выражения производственной функции выразим переменную , учитывая, что ,имеем чел.
Если стоимость основных фондов уменьшить в 100 раз, то
необходимая численность работников для сохранения
объемов производства, учитывая, что
составит:
человек.





























