Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Прямая

Содержание

ПРЯМАЯПрямая на чертеже может быть задана проекциями двух точек этой прямой (проекциями отрезка прямой)xk2k1A1A2В1В2
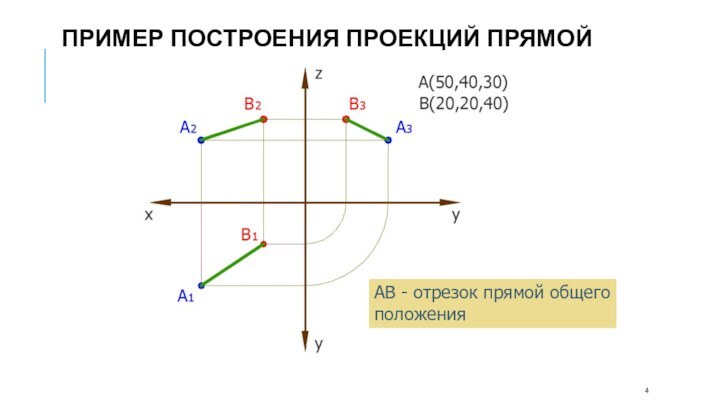
ПрямаяЛекция 2 ПРЯМАЯПрямая на чертеже может быть задана проекциями двух точек этой прямой (проекциями отрезка прямой)xk2k1A1A2В1В2 ПРЯМЫЕ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯПрямая общего положения не имеет проекций, параллельных или АВ - отрезок прямой общего положенияПример построения проекций прямой Вопрос 1Назовите способы задания отрезка прямой Прямая параллельная одной плоскости проекцийГоризонтальная прямая – параллельна горизонтальной плоскости проекцийФронтальная прямая АВ параллельна горизонтальной плоскости проекцийZ = constψ- угол между АВ и П2Горизонтальная прямая АВ параллельна фронтальной плоскости проекцийy = constφ – угол между АВ и П1Фронтальная прямая АВ параллельна профильной плоскости проекцийx = constПрофильная прямая Вопрос 2Какая из проекций фронтальной прямой дает её натуральную величину? Прямая параллельна двум плоскостям проекцийПрямая параллельна плоскостям П1и П2 , т.е. перпендикулярна АВ - горизонтально-проецирующая прямаяАВ перпендикулярна горизонтальной плоскости проекцийГоризонтально-проецирующая прямая АВ - фронтально-проецирующая прямаяАВ перпендикулярна фронтальной плоскости проекцийФронтально-проецирующая прямая АВ - профильно-проецирующая прямаяАВ перпендикулярна профильной плоскости проекцийПрофильно-проецирующая прямая ВОПРОС 3Какая из проекций горизонтальной прямой параллельна оси Х? Точки пересечения прямой линии с плоскостями проекции называются следами прямой Точка пересечения М - горизонтальный след прямой АВN - фронтальный след прямой АВСледы прямой N - фронтальный след прямой АВМ - горизонтальный след прямой АВСледы прямой ВОПРОС 4Задание: Построить следы прямой АВ Способы задания прямой1. По координатам точек концов отрезка прямой (проекциям отрезка прямой).2. 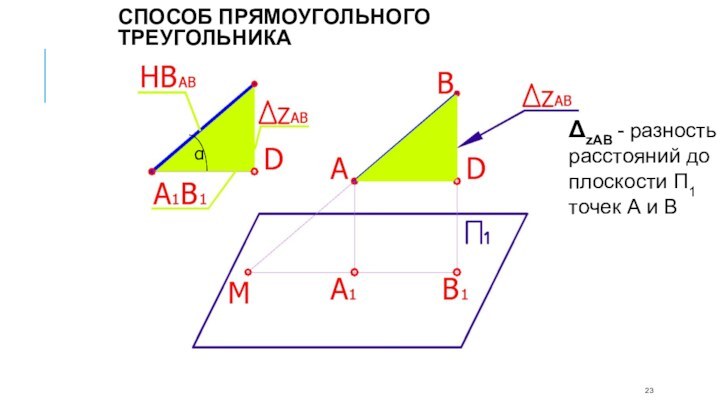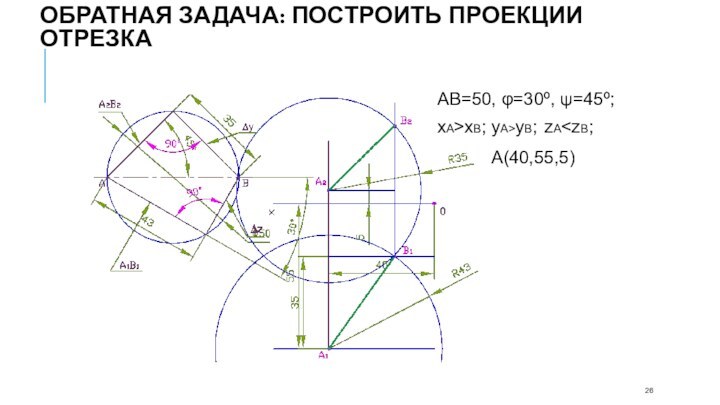Способ прямоугольного треугольникаНатуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, АВ - разность расстояний до плоскости  точек А и ВСпособ прямоугольного треугольника Способ прямоугольного треугольникаzАВ - разность расстояний до плоскости П1 точек А и В Дано: А₁В₁ и А₂В₂.Определить: НВАВ и углы наклона отрезка АВ к П₁ Способ прямоугольного треугольника. Обратная задачаЛекция 3 АВ=50, φ=30º, ψ=45º; xA>xB; yA>yB; zA Вопрос 5Для чего служит способ прямоугольного треугольника? По расположению относительно друг друга прямые могут:быть параллельнымипересекатьсяскрещиваться У скрещивающихся прямых k2k15251m и n - скрещивающиеся прямые1 и 2, 3 и 4 - По положению относительно плоскостей проекций различают:прямые общего положения (непараллельные и неперпендикулярные плоскостям ВЫВОДЫПрямые частного положения и их отрезки на соответствующих проекциях дают натуральные величины
Слайды презентации

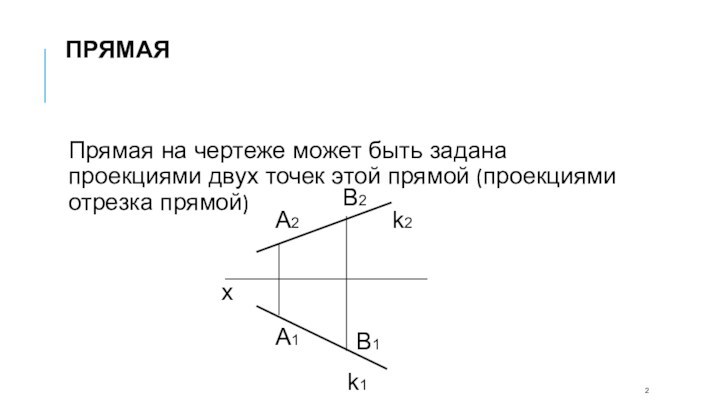
Слайд 2 ПРЯМАЯ
Прямая на чертеже может быть задана проекциями двух

ПРЯМАЯПрямая на чертеже может быть задана проекциями двух точек этой прямой (проекциями отрезка прямой)xk2k1A1A2В1В2

точек этой прямой (проекциями отрезка прямой)

x
k2
k1
A1
A2
В1
В2

Слайд 3 ПРЯМЫЕ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ
Прямая общего положения не

ПРЯМЫЕ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯПрямая общего положения не имеет проекций, параллельных

имеет проекций, параллельных или перпендикулярных осям координат
Прямые частного положения


Прямая параллельна одной плоскости проекций*
Прямая параллельна двум плоскостям проекций*
*В первом случае одна проекция отрезка прямой равна самому отрезку. Во втором случае две проекции отрезка равны ему

Слайд 4 АВ - отрезок прямой общего положения
Пример построения проекций

АВ - отрезок прямой общего положенияПример построения проекций прямой

прямой

Слайд 5 Вопрос 1
Назовите способы задания отрезка прямой

Вопрос 1Назовите способы задания отрезка прямой

Слайд 6 Прямая параллельная одной плоскости проекций
Горизонтальная прямая – параллельна

Прямая параллельная одной плоскости проекцийГоризонтальная прямая – параллельна горизонтальной плоскости проекцийФронтальная

горизонтальной плоскости проекций
Фронтальная прямая – параллельна фронтальной плоскости проекций
Профильная

прямая – параллельна профильной плоскости проекций
Перечисленные прямые также называют прямыми уровня

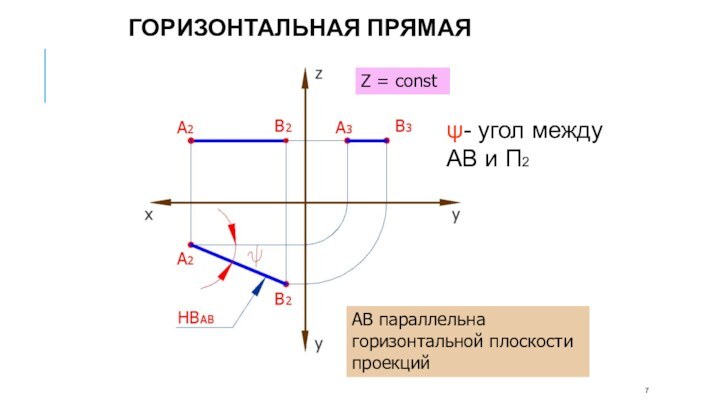
Слайд 7 АВ параллельна горизонтальной плоскости проекций
Z = const
ψ- угол

АВ параллельна горизонтальной плоскости проекцийZ = constψ- угол между АВ и П2Горизонтальная прямая

между АВ и П2
Горизонтальная прямая

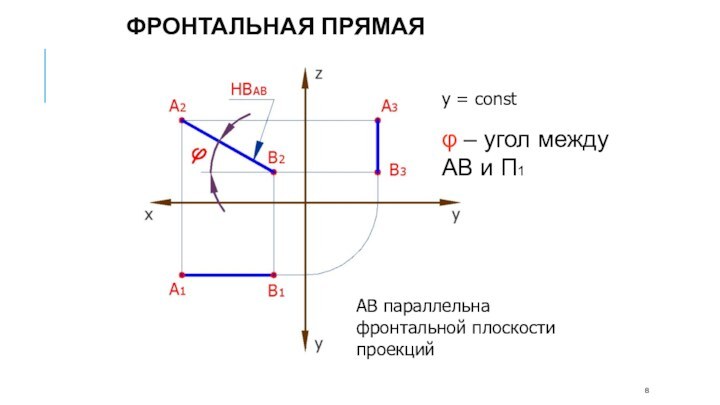
Слайд 8 АВ параллельна фронтальной плоскости проекций
y = const
φ –

АВ параллельна фронтальной плоскости проекцийy = constφ – угол между АВ и П1Фронтальная прямая

угол между АВ и П1
Фронтальная прямая

Слайд 9 АВ параллельна профильной плоскости проекций
x = const
Профильная прямая

АВ параллельна профильной плоскости проекцийx = constПрофильная прямая

Слайд 10 Вопрос 2
Какая из проекций фронтальной прямой дает её

Вопрос 2Какая из проекций фронтальной прямой дает её натуральную величину?

натуральную величину?

Слайд 11 Прямая параллельна двум плоскостям проекций
Прямая параллельна плоскостям П1и

Прямая параллельна двум плоскостям проекцийПрямая параллельна плоскостям П1и П2 , т.е.

П2 , т.е. перпендикулярна плоскости П3 – профильно-проецирующая прямая
Прямая

параллельна плоскостям П1 и П3 , т.е. перпендикулярна плоскости П2 – фронтально-проецирующая прямая
Прямая параллельна плоскостям П2 и П3 , т.е. перпендикулярна плоскости П1 – горизонтально-проецирующая прямая

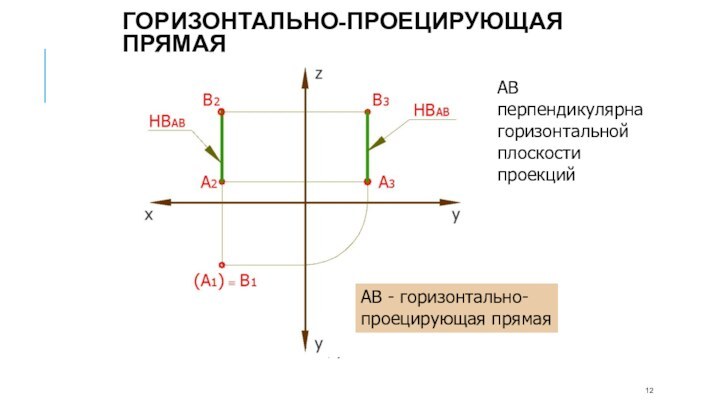
Слайд 12 АВ - горизонтально-проецирующая прямая
АВ перпендикулярна горизонтальной плоскости проекций
Горизонтально-проецирующая

АВ - горизонтально-проецирующая прямаяАВ перпендикулярна горизонтальной плоскости проекцийГоризонтально-проецирующая прямая

прямая

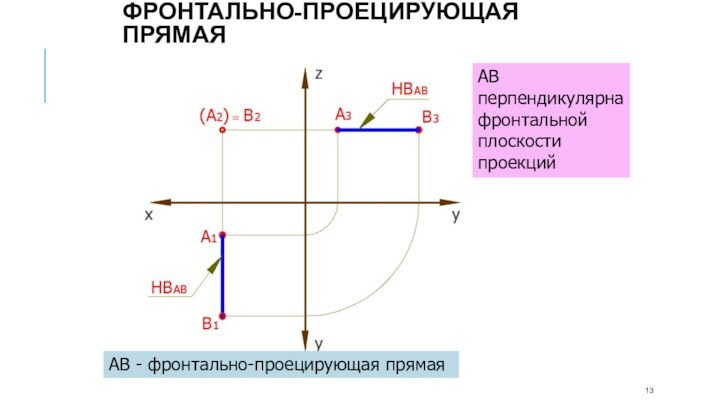
Слайд 13 АВ - фронтально-проецирующая прямая
АВ перпендикулярна фронтальной плоскости проекций
Фронтально-проецирующая

АВ - фронтально-проецирующая прямаяАВ перпендикулярна фронтальной плоскости проекцийФронтально-проецирующая прямая

прямая

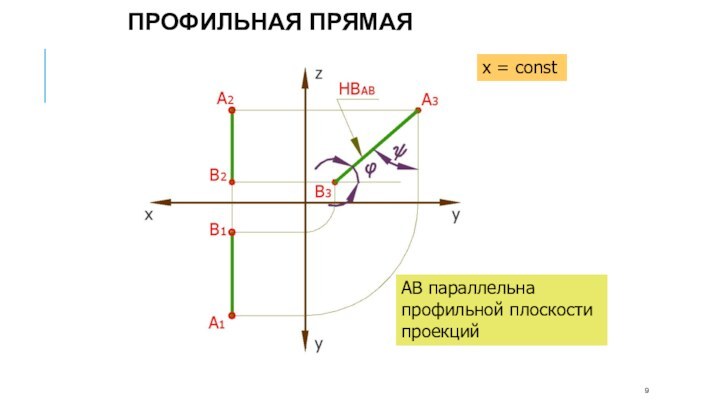
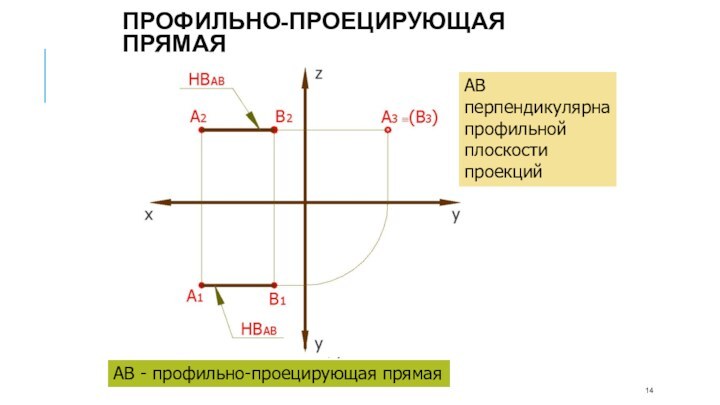
Слайд 14 АВ - профильно-проецирующая прямая
АВ перпендикулярна профильной плоскости проекций
Профильно-проецирующая

АВ - профильно-проецирующая прямаяАВ перпендикулярна профильной плоскости проекцийПрофильно-проецирующая прямая

прямая

Слайд 15 ВОПРОС 3
Какая из проекций горизонтальной прямой параллельна оси

ВОПРОС 3Какая из проекций горизонтальной прямой параллельна оси Х?

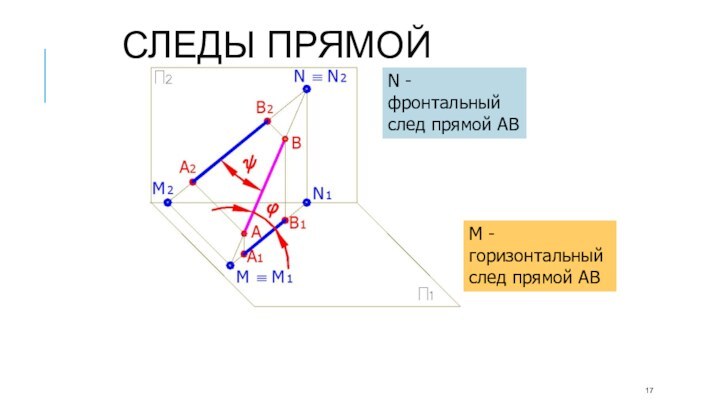
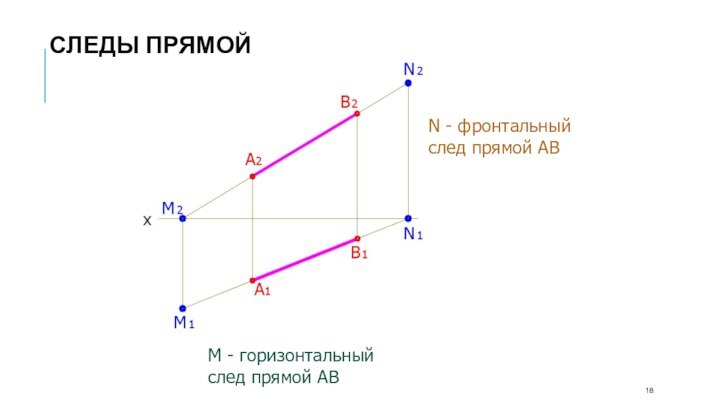
Слайд 16 Точки пересечения прямой линии с плоскостями проекции называются

Точки пересечения прямой линии с плоскостями проекции называются следами прямой Точка

следами прямой
Точка пересечения прямой с горизонтальной плоскостью проекций

называется горизонтальным следом прямой
Точка пересечения прямой с фронтальной плоскостью проекций называется фронтальным следом прямой

Следы прямой

Слайд 17 М - горизонтальный след прямой АВ
N - фронтальный

М - горизонтальный след прямой АВN - фронтальный след прямой АВСледы прямой

след прямой АВ
Следы прямой

Слайд 18 N - фронтальный след прямой АВ
М - горизонтальный

N - фронтальный след прямой АВМ - горизонтальный след прямой АВСледы прямой

след прямой АВ
Следы прямой

Слайд 19 ВОПРОС 4
Задание: Построить следы прямой АВ

ВОПРОС 4Задание: Построить следы прямой АВ

Слайд 20 Способы задания прямой
1. По координатам точек концов отрезка

Способы задания прямой1. По координатам точек концов отрезка прямой (проекциям отрезка

прямой (проекциям отрезка прямой).
2. Параметрами отрезка прямой линии:
-

натуральной величиной отрезка (НВ);
- углами наклона к плоскостям проекций -  (П₁) и  (П₂);
- угол между линией отрезка и горизонтальной плоскостью (П₁);
- угол между линией отрезка и фронтальной плоскостью (П₂).

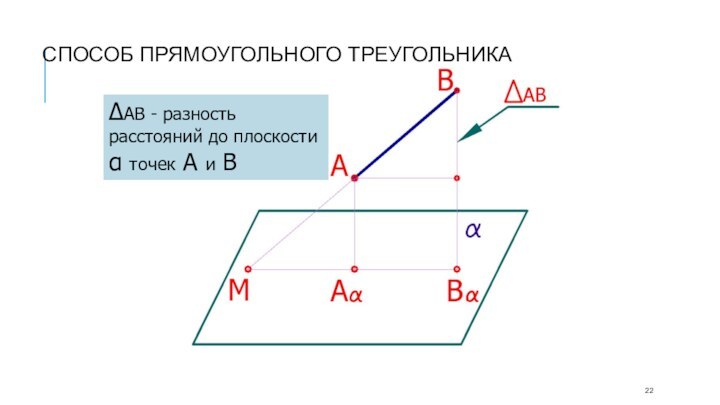
Слайд 21 Способ прямоугольного треугольника
Натуральная величина отрезка прямой общего положения

Способ прямоугольного треугольникаНатуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного

равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция

отрезка на любую плоскость проекций, другим – разность расстояний концов отрезка до той же плоскости проекций

Слайд 22 АВ - разность расстояний до плоскости  точек

АВ - разность расстояний до плоскости  точек А и ВСпособ прямоугольного треугольника

А и В
Способ прямоугольного треугольника

Слайд 23
Способ прямоугольного треугольника
zАВ - разность расстояний до плоскости

Способ прямоугольного треугольникаzАВ - разность расстояний до плоскости П1 точек А и В

П1 точек А и В

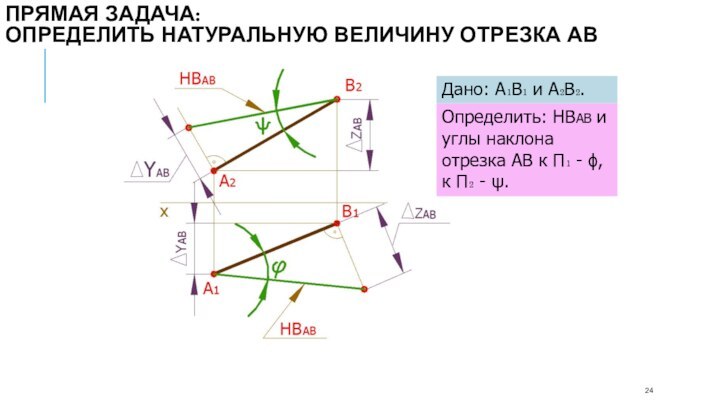
Слайд 24 Дано: А₁В₁ и А₂В₂.
Определить: НВАВ и углы наклона

Дано: А₁В₁ и А₂В₂.Определить: НВАВ и углы наклона отрезка АВ к

отрезка АВ к П₁ - , к П₂ -

.

Прямая задача: определить натуральную величину отрезка АВ

Слайд 25 Способ прямоугольного треугольника. Обратная задача
Лекция 3

Способ прямоугольного треугольника. Обратная задачаЛекция 3

Слайд 26 АВ=50, φ=30º, ψ=45º; xA>xB; yA>yB; zA

АВ=50, φ=30º, ψ=45º; xA>xB; yA>yB; zA

построить проекции отрезка

Слайд 27 Вопрос 5
Для чего служит способ прямоугольного треугольника?

Вопрос 5Для чего служит способ прямоугольного треугольника?

Слайд 28 По расположению относительно друг друга прямые могут:
быть параллельными
пересекаться
скрещиваться

По расположению относительно друг друга прямые могут:быть параллельнымипересекатьсяскрещиваться У скрещивающихся прямых

У скрещивающихся прямых одноименные проекции прямых пересекаются, но

точки пересечения не лежат на одной линии связи

Относительное положение прямых

Слайд 29 k2
k1
52
51
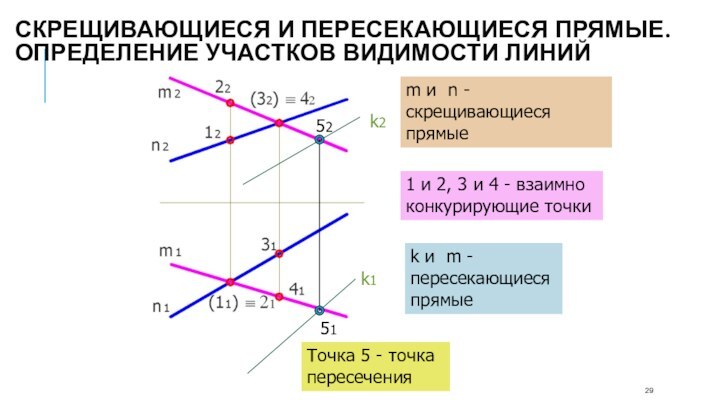
m и n - скрещивающиеся прямые
1 и 2,

k2k15251m и n - скрещивающиеся прямые1 и 2, 3 и 4

3 и 4 - взаимно конкурирующие точки
k и m

- пересекающиеся прямые

Точка 5 - точка пересечения

Скрещивающиеся и пересекающиеся прямые. Определение участков видимости линий

Слайд 30 По положению относительно плоскостей проекций различают:
прямые общего положения

По положению относительно плоскостей проекций различают:прямые общего положения (непараллельные и неперпендикулярные

(непараллельные и неперпендикулярные плоскостям проекций)
прямые частного положения: параллельные

или перпендикулярные плоскостям проекций
Способ прямоугольного треугольника позволяет решать метрические и позиционные задачи в отношении отрезков прямой общего положения

ВЫВОДЫ

  • Имя файла: pryamaya.pptx
  • Количество просмотров: 76
  • Количество скачиваний: 0
- Предыдущая Дефицит йода
Следующая - Собаки-спасатели

Похожие презентации

Макраме в современной жизни Макраме в современной жизни 172
Презентация День матери в детском саду презентация к уроку (средняя группа) Презентация День матери в детском саду презентация к уроку (средняя группа) 219
angel iz azhurnyh salfetok angel iz azhurnyh salfetok 57
Пошаговая инструкция Пошаговая инструкция 82
Кукольный театр своими руками презентация Кукольный театр своими руками презентация 108
Чарльз Бэббидж Чарльз Бэббидж 126
кіріспе кіріспе 120
Повышение качества железорудных окатышей с применением комплексных ферритных добавок Повышение качества железорудных окатышей с применением комплексных ферритных добавок 97
9 maya 9 maya 104
ПК 4.2. Предметно-развивающая среда учебного кабинета начальных классов материал по теме ПК 4.2. Предметно-развивающая среда учебного кабинета начальных классов материал по теме 88
Изменение предметно-пространственной среды по теме недели Дикие животные материал (средняя группа) Изменение предметно-пространственной среды по теме недели Дикие животные материал (средняя группа) 123
Презентация к проекту Экскурсия по посёлку Хор Презентация к проекту Экскурсия по посёлку Хор 197
prezentatsiya prezentatsiya 153
презентация снеговики к НОД Мама для снеговика презентация к занятию по конструированию, ручному труду (младшая группа) по теме презентация снеговики к НОД Мама для снеговика презентация к занятию по конструированию, ручному труду (младшая группа) по теме 36
Педагогические технологии на основе эффективности управления и организации учебного процесса методическая разработка Педагогические технологии на основе эффективности управления и организации учебного процесса методическая разработка 125
Уроки и презентации по православию план-конспект урока Уроки и презентации по православию план-конспект урока 99
Информационно -творческий проект Полетели в космос презентация к занятию (средняя группа) по теме Информационно -творческий проект Полетели в космос презентация к занятию (средняя группа) по теме 95
Консультация для родителей будущих первоклассников. Скоро в школу! консультация (1 класс) Консультация для родителей будущих первоклассников. Скоро в школу! консультация (1 класс) 110
Презентация Декоративное творчество презентация к занятию (средняя группа) Презентация Декоративное творчество презентация к занятию (средняя группа) 93
Целеполагание урока по УД ОГСЭ цикла в соответствии с ФГОС СПО Целеполагание урока по УД ОГСЭ цикла в соответствии с ФГОС СПО 118
ПАРНИКОВЫЙ ЭФФЕКТ ПАРНИКОВЫЙ ЭФФЕКТ 147
Презентация по черчению Правила оформления чертежей Презентация по черчению Правила оформления чертежей 102
От пятилетнего ребенка до меня только шаг презентация к занятию (младшая группа) по теме От пятилетнего ребенка до меня только шаг презентация к занятию (младшая группа) по теме 109
sobr sobr 104
Презентация Чьи пельмени лучше? по ПМ.02 Презентация Чьи пельмени лучше? по ПМ.02 143
Методическое портфолио презентация Методическое портфолио презентация 308
правила о ПДД правила о ПДД 40
Экскурсия Экскурсия 122
Надання першої долікарськоїдопомоги. Надання першої долікарськоїдопомоги. 91
Витамин В₂(Рибофлавин)-vitaminumВ₂(riboflavinum) Витамин В₂(Рибофлавин)-vitaminumВ₂(riboflavinum) 93