Слайд 2
В традиционной школе считается, что ученики должны сначала
выучить (запомнить) то, что предлагают учитель и учебник, затем
понять, а потом научиться применять полученные знания. Основной смысл учения детей состоит в усвоении этого знания.
Дидактическая система, применяемая в учебниках Петерсон,позволяет учителю на уроках по разным учебным предметам системно включать учащихся в учебную деятельность, где протекают процессы мотивации, построения и коррекции способов действий, реализации нормы и рефлексии, самоконтроля и самооценки, коммуникативного взаимодействия и др.
Слайд 6
Обучение по учебнику Л.Г. Петерсон строится на основе
деятельностного метода, который включает этапы урока:
постановка учебной задачи;
открытие детьми нового знания;
первичное закрепление (с комментированием);
самостоятельная работа с проверкой в классе (решение задач на повторение);
решение тренировочных упражнений;
контроль.
Слайд 8
Одной из важнейших целей в процессе обучения решению
текстовых задач является развитие умения моделировать задачу
с помощью
схем. Использование
схем особенно
удобно для задач с большими
числами, когда непосредственный
рисунок сделать трудно или даже невозможно.. Составление схемы к условию задачи позволяет наглядно её представить и осознанно определить план решения, что способствует успешному решению
Слайд 9
Обращаем Ваше внимание, что одной из особенностей программы Л.Г. Петерсон
по математике является обучение учащихся решению задач именно с помощью
схем. Схема к задаче позволяет учащимся подробно разобраться в ее условии и выйти на способ решения задачи. В «Методических рекомендациях для учителя» к каждому учебнику математики подробно описана эта система работы над задачами.
Слайд 11
Алгоритм решения задачи
Прочитай задачу.
Определи , о чем говорится
в задаче.
Определи тип задачи.
Составь план решения в зависимости от
типа задачи.
Запиши решение.
Подумай, можно ли решить задачу другим способом.
Проверь решение.
Запиши ответ.
Слайд 13
Приемы работы со схемами
1) самостоятельно «одеть» схему;
2) составить
задачу по схеме;
3) выбрать схемы к задачам;
4) комментирование задачи
только по схеме (без данных);
5) соединить схемы с подходящим выражением.
Составление схемы к условию задачи позволяет наглядно её представить и осознанно определить план решения, что способствует успешному решению.
Слайд 14
Формы работы над задачей
Работа над решенной задачей. Многие
учащиеся только после повторного анализа осознают план решения задачи.
Представление ситуации, описанной в задаче (нарисовать «картинку»). Учитель обращает внимание детей на детали, которые нужно обязательно представить, а которые можно опустить. Мысленное участие в этой ситуации. Разбиение текста задачи на смысловые части. Моделирование ситуации с помощью чертежа, рисунка.
Слайд 15
Самостоятельное составление задач учащимися. Составить задачу:
1) используя слова
«больше на», «столько», «сколько», «меньше в 2, «настолько больше»,
«настолько меньше»;
2) решаемую в 1, 2, 3 действия;
3) по данному ее плану решения, действиям и опыту;
4) по выражению и т. д.
Решение задач с недостающими или лишними данными.
Изменение вопроса задачи.
Составление различных выражений по данным задачи и объяснение, что обозначает то или иное выражение. Выбрать те выражения, которые являются ответом на вопрос задачи.
Использование приема сравнения задач и их решения.
Запись двух решений на доске – одного верного и другого неверного.
Слайд 16
Какой вопрос и какое действие лишние в решении
задачи (или наоборот, восстановить пропущенный вопрос и действие в
задаче.)
Составление аналогичной задачи с измененными данными.
Решение обратных задач.
Решение задачи алгебраическим и арифметическим способом.
Систематическое использование на уроках математики и внеурочных занятиях специальных задач, направленных на развитие логического мышления, расширяет математический кругозор младших школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.
Слайд 17
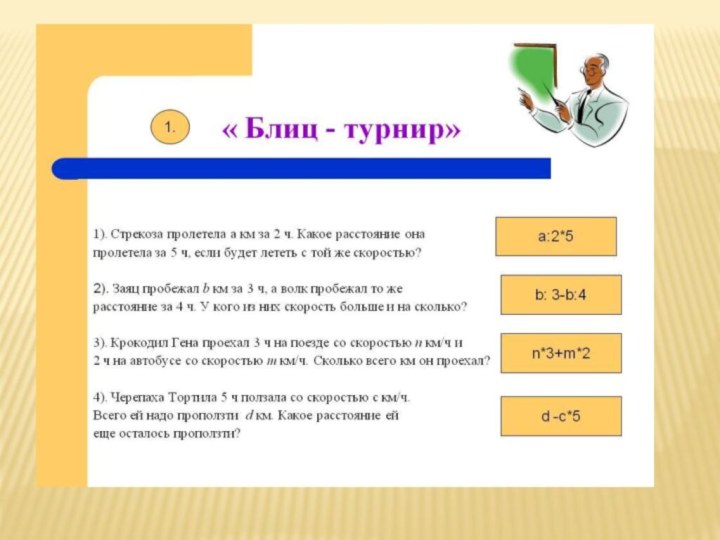
Работа с «Блиц-турнирами»
«БЛИЦ»: его значение – очень быстрый,
проводимый за короткое время.
Поэтому, действительно, здесь надо продумать вопросы
наличия у ребят черновиков, где схемы, таблицы, рисунки они смогли бы выполнить быстро, «от руки».
Далее очень важно , чтобы эти упражнения выполнялись в классе с тем, чтобы ребята смогли проконтролировать свою работу и скорректировать её, если возникли ошибки: учитель даёт возможность это сделать с помощью подробного образца выполнения задания.
Слайд 19
Если в классе ребята с низким или средним
уровнем подготовленности, то предложите выполнять не все шесть задач
на время, а первые три (они, как правило, являются стандартными), а в дальнейшем наращивайте объём. При организации работы с задачами можно обойтись без вычислений, ограничиваясь только выражением, и даже больше – только составлением схемы по условию задач. А ещё помогают такие формы работы, как работа в парах или в группах (создаются комфортные условия, когда ребята могут выразить свои затруднения вслух (вопрос обсуждается внутри группы или вопрос выносится на обсуждение с классом), а, значит, и это главное, знание усваивается осознанно).
Слайд 20
АЛГЕБРАИЧЕСКИЙ СПОСОБ РЕШЕНИЯ ЗАДАЧИ
Слайд 21
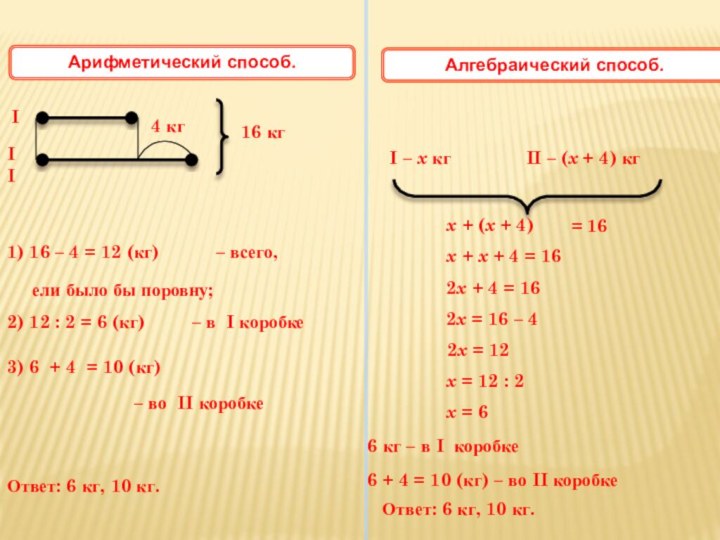
4 кг
1) 16 – 4 = 12 (кг)
I
II
16
кг
– всего,
ели было бы поровну;
2) 12 : 2 =
6 (кг)
– в I коробке
3) 6 + 4 = 10 (кг)
– во II коробке
Ответ: 6 кг, 10 кг.
Арифметический способ.
I – x кг
II – (x + 4) кг
x + (x + 4)
= 16
x + x + 4 = 16
2x + 4 = 16
2x = 16 – 4
2x = 12
x = 12 : 2
x = 6
6 кг – в I коробке
6 + 4 = 10 (кг) – во II коробке
Ответ: 6 кг, 10 кг.
Алгебраический способ.
Слайд 22
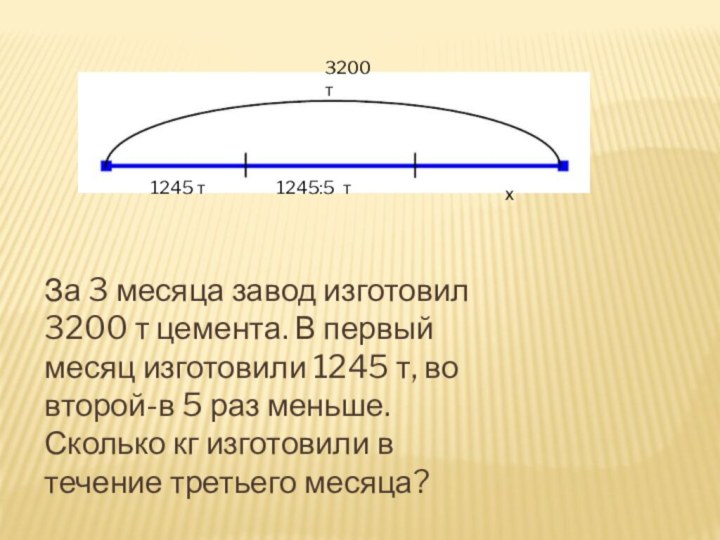
За 3 месяца завод изготовил 3200 т цемента.
В первый месяц изготовили 1245 т, во второй-в 5
раз меньше. Сколько кг изготовили в течение третьего месяца?
3200 т
1245 т
1245:5 т
х
Слайд 23
1245+1245:5+х=3200
1245+249+х=3200
1494+х=3200
х=3200-1494
х=1706
Ответ: 1706 т
8 · х = 24 (у -
4) · 3=15
« Уравнения»
х + 768 : 2
6 : В > 66
Слайд 25
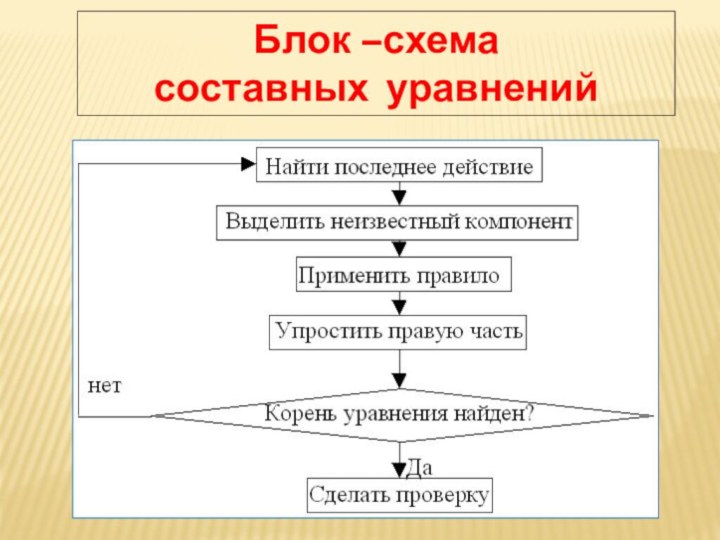
Блок –схема
составных уравнений































![Презентация по обучению грамоте на тему Согласные звуки [л], [л’]. Буквы Лл.](/img/tmb/6/599955/861409a8bbb832b417a51db7c6c49463-210x.jpg)














