Слайд 2
Литература
Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на
базе средней школы.– М.: Наука, 1989.
Красс М.С., Чупрынов
Б.П. Математика для экономистов.– СПб.: Питер, 2007
Лунгу К.Н. Линейное программирование. Руководство к решению задач. – М.:ФИЗМАТЛИТ, 2005
Математика для техникумов.
Алгебра и начала анализа. Под ред. Г.Н. Яковлева. Ч.2 – М.: Наука. 1988
Слайд 3
Матрицы
и действия над ними
Слайд 4
Матрицы и действия над ними
Определение
Матрицей называется система
m
n элементов, расположенных в прямоугольной таблице
из m
строк и n столбцов.
Элементами матрицы могут быть числа, функции, символы к которым применимы алгебраические операции
Слайд 6
Термины и обозначения
Элемент матрицы aik
i – номер
строки (от 1 до m)
k – номер столбца (от
1 до n)
Матрица называется квадратной, если количество строк равно количеству столбцов (m = n)
Слайд 7
Термины и обозначения
Строчная матрица (m = 1)
Столбцовая матрица (n = 1)
Слайд 8
Термины и обозначения
Диагональная матрица (m =
n и ненулевые элементы расположены только на главной диагонали)
Слайд 9
Термины и обозначения
Единичная матрица (диагональная матрица,
ненулевые элементы которой равны единице)
Е =
Слайд 10
Термины и обозначения
Симметричная матрица aik =
aik (элементы, симметричные относительно главной диагонали, равны)
Нулевая матрица
aik = 0
(все элементы матрицы равны нулю)
Слайд 11
Термины и обозначения
Транспонирование матрицы (поменять местами
строки
и столбцы )
Ат =
Слайд 12
Действия над матрицами
Сложение (вычитание) матриц
Действие определено только
для матриц одинакового размера
А =
В =
Слайд 13
Действия над матрицами
Сложение (вычитание) матриц
C = А
B =
=
Cik = Aik Bik
Слайд 14
Действия над матрицами
Умножение матрицы на число
В =
А =
=
Вik = Aik
На умножаются все элементы матрицы
Слайд 15
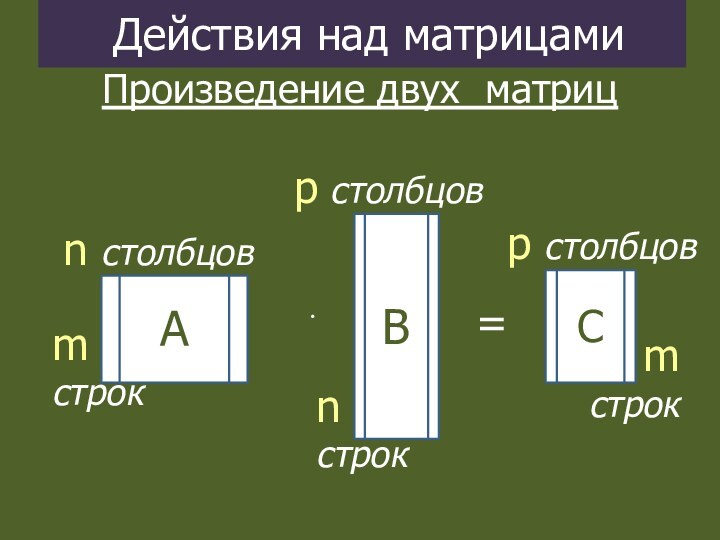
Действия над матрицами
Произведение двух матриц
Произведение имеет смысл
для квадратных матриц одинакового размера, либо для прямоугольных матриц,
где:
число столбцов матрицы А равно числу строк матрицы В
C = А B
Слайд 16
Действия над матрицами
Произведение двух матриц
p столбцов
Слайд 17
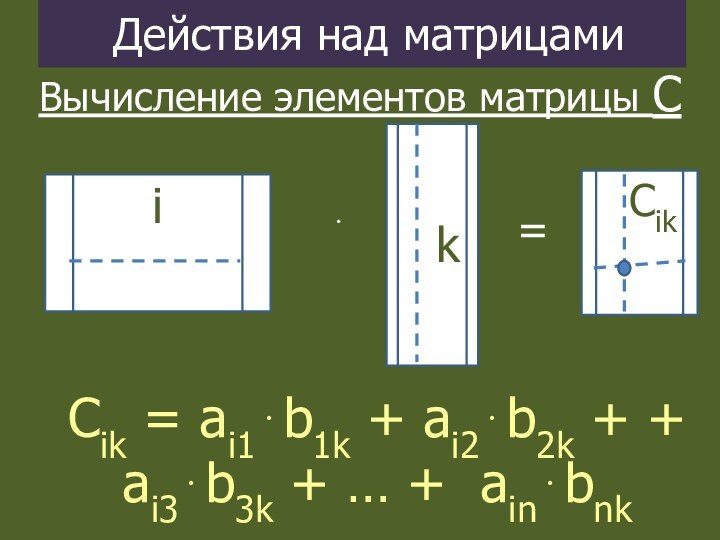
Действия над матрицами
Вычисление элементов матрицы С
Элемент Сik
равен сумме произведений элементов
i-й строки матрицы А на
k-й столбец матрицы В
Слайд 18
Действия над матрицами
Вычисление элементов матрицы С
Сik =
ai1b1k + ai2b2k + + ai3b3k + … +
ainbnk
Слайд 19
Действия над матрицами
С11 = 16 + 27
+ 38 = 44
С12 = 1(-3) + 21 +
37 = 20
С21 = 26 + (-4)7 + 58 = 24
С22 = 2(-3) + (-4)1 + 57 = 25
Слайд 20
Действия над матрицами
Частный случай:
произведение строчки на
столбец дает один элемент, при этом число столбцов матрицы
А должно равняться числу строк матрицы В
=
Слайд 21
Действия над матрицами
Частный случай:
произведение столбца на
строчку имеет смысл всегда, при этом число строк матрицы
С равно числу строк матрицы А и число столбцов матрицы С равно числу столбцов матрицы В
=
Слайд 22
Действия над матрицами
Свойство произведения матриц
В общем случае
АВ ВА
Если АВ = ВА, то такие матрицы
называются перестановочными или коммутирующими.
Для квадратных матриц
АЕ = ЕА = А
где Е – единичная матрица
Слайд 23
Действия над матрицами
Пример
А =
В =
Ответ
АВ =
ВА
=
Найти АВ и ВА
Слайд 24
Запись в матричной форме линейных уравнений
2х1 – 3х2
+ х3 = 3
4х1 + х2
= 8
3х1 + 4х2 + 2х3 = 20
=
Слайд 25
Запись в матричной форме линейных уравнений
=
А
Х
В
АХ = В
, откуда Х = А-1В
Слайд 26
Функции EXCEL для работы с матрицами
ТРАНСП() МУМНОЖ()
МОБР()
Порядок работы
Записать исходную матрицу.
Выделить область ячеек для помещения
результата.
Выбрать нужную функцию и записать аргументы.
Завершить командой матричной операции Ctrl + Shift + Enter.
Слайд 27
Домашнее задание
Выучить конспект лекции.
Учебник Красс М.С., Чупрынов
Б.П. Математика для экономистов.– СПб.: Питер, 2007
§ 1.2.1, 1.2.2,
1.2.3, 1.2.4
Подготовится к практической работе № 1
«Действия с матрицами»
Слайд 29
Определители
Определителем называется число, соответствующее квадратной матрице.
Число есть сумма
n! произведений элементов матрицы n-го порядка, взятых по одному
из каждой строчки и каждого столбца.
Знак каждого произведения определяется особым правилом.
Слайд 30
Определители
А =
|А| = = det A =
Обозначения
Слайд 31
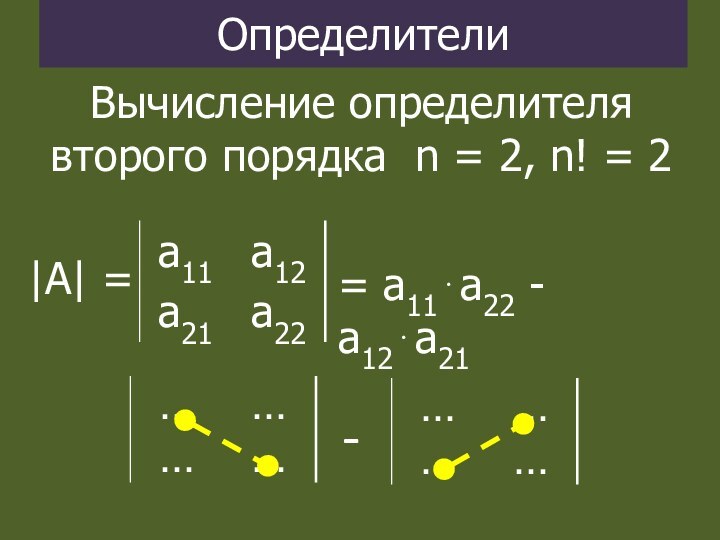
Определители
|А| =
Вычисление определителя второго порядка n = 2,
n! = 2
= a11a22 - a12a21
-
Слайд 32
Определители
|А| =
Вычисление определителя третьего порядка n = 3,
n! = 6
= a11a22 а33 + a12a23 а31
+ a13a21 а32 - a13a22 а31 - a12a21 а33 - a11a23 а32
=
Слайд 33
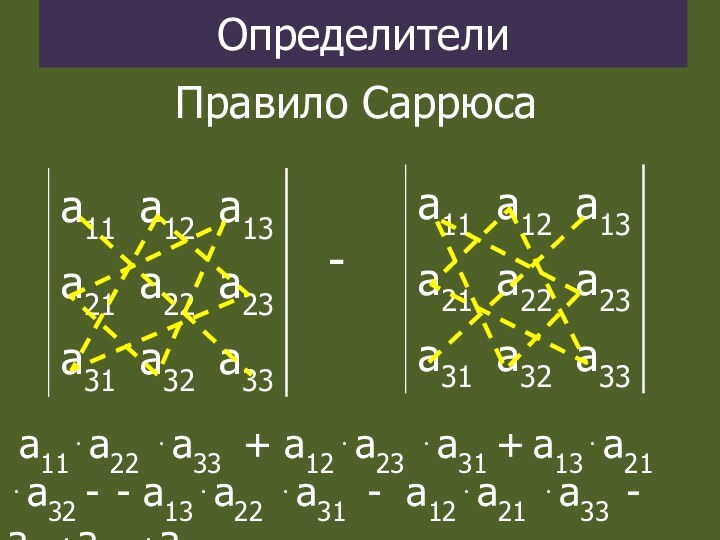
Определители
Правило Саррюса
-
a11a22 а33 + a12a23 а31 +
a13a21 а32 - - a13a22 а31 - a12a21 а33
- a11a23 а32
Слайд 34
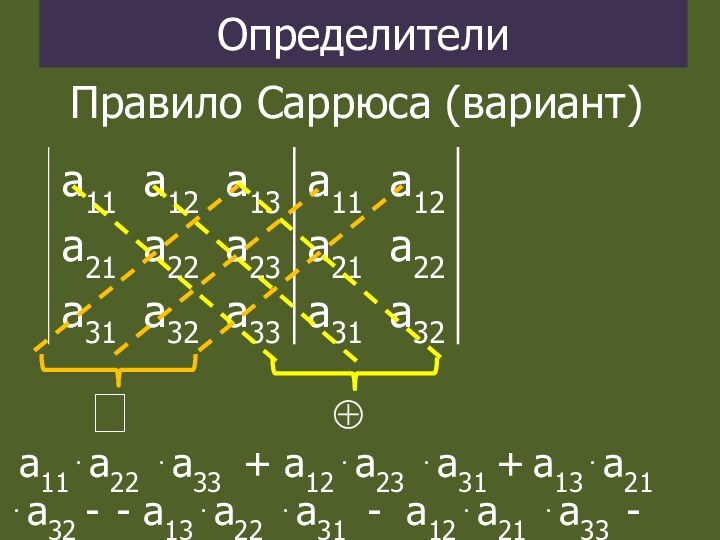
Определители
Правило Саррюса (вариант)
a11a22 а33 + a12a23 а31
+ a13a21 а32 - - a13a22 а31 - a12a21
а33 - a11a23 а32
Слайд 35
Определители
Пример
=
= 5 – 8 + 12
– (-3 + 8 +20) = -16
Слайд 36
Минор элемента определителя
Минором какого либо элемента определителя называется
определитель, полученный из данного, путем вычеркивания строки и столбца,
на пересечении которых стоит элемент.
Слайд 37
Минор элемента определителя
Пример: минор к элементу а11
=
М11
=
М22 =
Слайд 38
Алгебраическое дополнение
Алгебраическим дополнением элемента определителя называется его минор,
взятый со своим или противоположным знаком согласно правилу: если
сумма номеров столбца и строки – четная, то минор берется со своим знаком, если нечетная то с противоположным.
Слайд 39
Алгебраическое дополнение
Для выполнения этого правила перед минором записывается
множитель
(- 1)(i + k)
Теорема
Определитель любого порядка равен сумме произведений
элементов любой строки (столбца) на их алгебраические дополнения.
Слайд 40
Алгебраическое дополнение
Для определителя 3-го порядка
разложение по 1-й
строке:
= (-1)1+1 a1
+
+ (-1)1+2 b1
+
(-1)1+3 c1
Второе слагаемое берется
со знаком минус!
Слайд 41
Свойства определителей
Значение определителя при его транспонировании не изменяется.
При
перестановке двух столбцов (строк) знак определителя изменяется на противоположный.
Определитель
с двумя одинаковыми строками (столбцами) равен нулю.
Слайд 42
Множитель общий для некоторого столбца (строки) может быть
вынесен за знак определителя.
Значение определителя не изменяется, если к
элементам некоторого столбца (строки) прибавить элементы другого столбца (строки), при этом прибавляемые элементы можно умножать на один и тот же ненулевой множитель.
Слайд 43
Свойства определителей
Указанные свойства упрощают вычисление определителей.
2
-3
=
=
Раскладываем по
второму столбцу:
= (-1)1+2 (-2)
=
60
Слайд 44
Функция EXCEL для работы с определителем
МОПРЕД()
Порядок работы
Записать определитель.
Выделить
одну ячейку для помещения результата.
Выбрать функцию МОПРЕД() и записать
аргумент.
Завершить командой ОК или Enter. (Операция не матричная!)
Слайд 45
Обратная матрица
Обратная матрица А-1 к квадратной матрице А
существует только тогда, когда определитель |A| 0
Вычисление обратной
матрицы связано с нахождением присоединенной (взаимной) матрицы
Слайд 46
Обратная матрица
Присоединенной матрицей называется матрица, составленная из алгебраических
дополнений к исходной, в строчках которой расположены соответствующие элементы
столбцов (транспонированная)
Обозначение : Ấ или А
Слайд 48
Обратная матрица
А11 =
и т.д.
А21 =
Слайд 49
Обратная матрица
Теорема
Для присоединенной матрицы А к квадратной матрицы
А n-го порядка справедливо тождество
А А = А
А = |А| Е
Следствие:
Слайд 50
Обратная матрица
А =
А11 = 6 А12 =
- 4 А21 = - 7 А22
= 5
Найти А-1
|А| = 30 – 28 = 2 0
А-1 = ½
=
Слайд 51
Вычисление обратной матрицы в EXCEL
Записать исходную матрицу.
Выделить область
ячеек для обратной матрицы и задать формат ячеек –
дробный.
Выбрать функцию МОБР() и записать аргумент.
Завершить командой матричной операции Ctrl + Shift + Enter.
Слайд 52
Домашнее задание
Выучить конспект лекции.
Красс М.С., Чупрынов Б.П.
Математика для экономистов.– СПб.: Питер, 2007. §§ 1.3.1, 1.3.2, 1.3.3
, 1.2.7, 1.5.1, 1.5.2
Подготовится к практической работе № 2 «Вычисление определителей, обратных матриц».
Слайд 54
Системы линейных уравнений
а11х1 + а12х2 + … +
а1nхn = b1
… … + aikхk +…
= bi
an1х1 + an2х2 + … + annхn = bn
Постановка задачи
Найти решение системы n уравнений с n неизвестными
(х1, х2 … xn)
Слайд 55
Системы линейных уравнений
Обозначения:
Хk (k = 1, 2, …
n) – неизвестные
аik , bi – коэффициенты
i – порядковый
номер уравнения
k – порядковый номер неизвестной
Слайд 56
Системы линейных уравнений
Система, имеющая хотя бы одно решение,
называется совместной.
Система, не имеющая решений, называется несовместной.
Система, имеющая
единственное решение, называется определенной.
Система, имеющая множество решений, называется неопределенной.
Слайд 57
Системы линейных уравнений
Теорема Крамера
Если определитель системы n уравнений
с n неизвестными не равен нулю, то система совместна
и имеет единственное решение:
Слайд 58
Системы линейных уравнений
где:
D – определитель, составленный из
коэффициентов аik
D1, D2 … DN - определитель,
полученный из D путем замены k-го столбца столбцом коэффициентов bi
Слайд 59
Системы линейных уравнений
3х1 + 2х2 + х3 =
5
2х1 - х2 + х3 = 6
х1
+ 5х2 = - 3
=
D =
-1
=
= (-1)3+11
= -5 + 3 = -2 0
Пример:
Слайд 60
Системы линейных уравнений
=
D1 =
-1
=
= (-1)3+11
= 5 - 9
= - 4
Слайд 61
Системы линейных уравнений
=
D2 =
=
= (-1)3+11
= 3 - 1
Слайд 62
Системы линейных уравнений
=
D3 =
5
=
= (-1)2+2(-1)
= -189 +187 =
-2
2
Слайд 63
Системы линейных уравнений
=
= 2
=
= - 1
=
=
Слайд 64
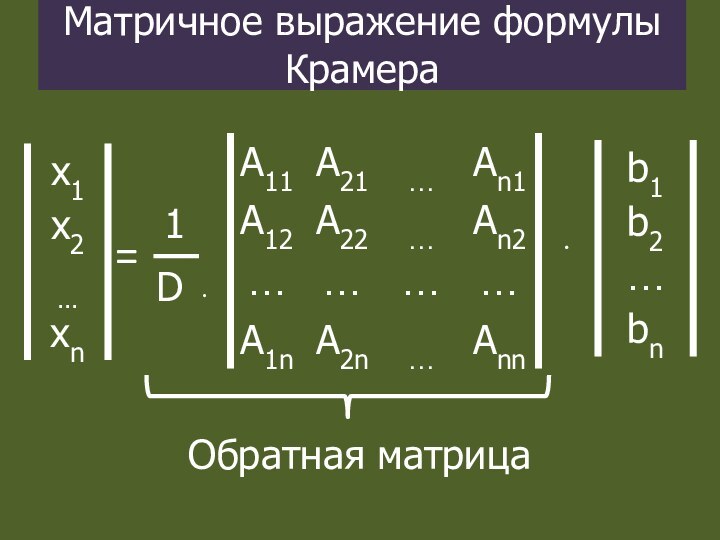
Матричное выражение формулы Крамера
=
А
Х
В
АХ = В , откуда
Х = А-1В
Слайд 65
Матричное выражение формулы Крамера
=
Обратная матрица
Слайд 66
Реализация матричного выражения формулы Крамера в EXCEL
Записать матрицу
коэффициентов и матрицу свободных членов уравнения.
Выделить квадратную область и
найти обратную матрицу (МОБР)
Выделить столбец результата и поместить туда произведение обратной матрицы на матрицу коэффициентов (МУМНОЖ)
Слайд 67
Матричное выражение формулы Крамера
А =
В =
Тот
же пример:
Слайд 68
Матричное выражение формулы Крамера
=
=
=
Ответ:
х1 = 2
х2 =
- 1
х3 = 1
Слайд 69
Системы линейных уравнений
Решение системы линейных уравнений методом исключения
неизвестных (метод Гаусса)
Метод основан на преобразовании расширенной матрицы коэффициентов
уравнения в трапециевидную:
Слайд 71
Системы линейных уравнений
и затем последовательному нахождению (хn ,
хn-1 … x2 , x1)
Подставляя найденное значение хn в
предыдущую строку, находим хn-1 и т.д., до нахождения x1
Слайд 72
Системы линейных уравнений
При преобразовании расширенной матрицы коэффициентов уравнения
в трапециевидную, используются следующие действия, обеспечивающие равносильность исходной и
преобразованной системы уравнений:
Слайд 73
Системы линейных уравнений
Умножение какой-либо строки на ненулевой множитель.
Прибавление
к какой-либо строке другой строки, в том числе умноженной
на ненулевой множитель.
Перестановка любых строк расширенной матрицы.
Слайд 74
Системы линейных уравнений
3х1 + 2х2 + х3 =
5
2х1 - х2 + х3 = 6
х1
+ 5х2 = - 3
Пример:
-3
=
=
Составляем матрицу и преобразуем к диагональному виду :