Слайд 2
Средняя величина
— это обобщающий показатель, характеризующий совокупности
однотипных явлений по какому-либо количественному варьирующему признаку.
Средняя всегда
обобщает количественную вариацию признака, т. е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами.
Средние величины делятся на два больших класса:
степенные средние,
структурные средние.
Слайд 3
К степенным средним относятся
средняя геометрическая;
средняя гармоническая;
средняя арифметическая;
средняя квадратическая;
средняя
кубическая.
Слайд 4
Степенные средние могут быть простыми и взвешенными
Простая средняя
считается по несгруппированным данным и имеет следующий общий вид:
где
х — меняющая величина признака;
m — показатель степени средней;
n — число вариант.
Слайд 5
Степенные средние взвешенные
Взвешенная средняя считается по сгруппированным данным
и имеет общий вид:
где хi — варианта (значение) осредняемого
признака или серединное значение интервала, в котором измеряется варианта;
m — показатель степени средней;
fi — частота, показывающая, сколько раз встречается i-e значение осредняемого признака.
Слайд 6
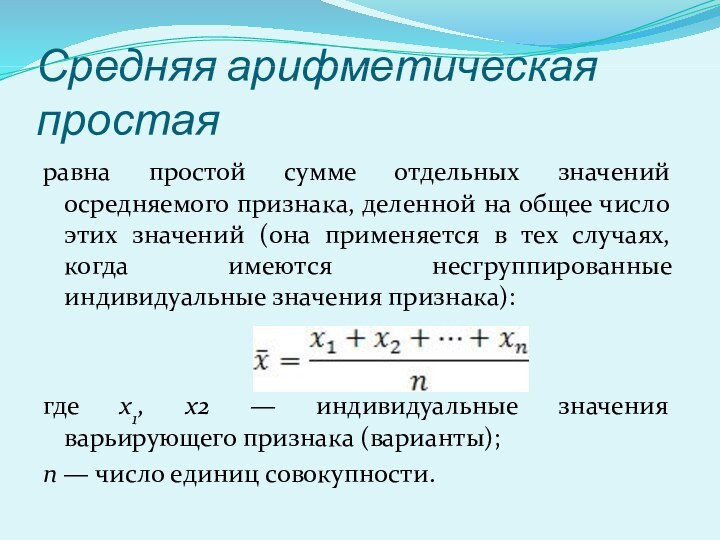
Средняя арифметическая простая
равна простой сумме отдельных значений
осредняемого признака, деленной на общее число этих значений (она
применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):
где х1, х2 — индивидуальные значения варьирующего признака (варианты);
п — число единиц совокупности.
Слайд 7
Средняя арифметическая взвешенная
средняя сгруппированных величин х1 ,
х2 — вычисляется по формуле:
где f1, f2, ..,fn —
веса (частоты повторения одинаковых признаков);
∑xf — сумма произведений величины признаков на их частоты;
∑f— общая численность единиц совокупности.
Слайд 8
Структурные средние –
мода и медиана.
Модой в
статистике называют величину признака которая чаще всего встречается в
данной совокупности. В вариационном ряду это будет варианта имеющая наибольшую частоту.
Медианой в статистике называют величину варианта которая находится в середине вариационного ряда. Она делит ряд пополам, т.е. по обе стороны от неё находятся одинаковое количество единиц совокупности.
Слайд 9
Мода вычисляется по формуле:
где XMo - нижняя граница
модального интервала;
i o – величина модального интервала;
fMo-1
– частота интервала предшествовшего модальному;
f Mo – частота модального интервала;
fMo+1 – частота интервала следующего за модальным.
Слайд 10
Значение медианы вычисляется по формуле:
где XMe -
начальное значение медианного интервала;
iMe – величина медианного интервала;
f – сумма частот ряда;
SMe-1 – сумма накопительных частот в интервале предшествующих медианному;
fMe – частота медианного интервала.
Слайд 11
Вариация
это различие в значениях какого-либо признака у
разных единиц данной совокупности в один и тот же
период или момент времени.
Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.
Слайд 12
К показателям вариации относятся:
размах вариации;
среднее линейное
отклонение;
дисперсия;
среднее квадратическое отклонение;
коэффициент вариации;
коэффициент постоянства.
Слайд 13
Размах вариации (R)
представляет собой разность между максимальным и
минимальным значениями признака:
R = Xmах - Xmin
Слайд 14
Среднее линейное отклонение d
представляет собой среднюю арифметическую
абсолютных значений отклонений отдельных вариантов от их средней
для несгруппированных
данных
где n — число членов ряда;
для сгруппированных данных
где ∑ f — сумма частот вариационного ряда.
Слайд 15
Дисперсия признака
представляет собой средний квадрат отклонений вариантов
от их средней величины, она вычисляется по формулам:
для несгруппированных
данных
для сгруппированных данных
Слайд 16
Среднее квадратическое отклонение
показывает, насколько в среднем отклоняются
конкретные варианты от их среднего значения.
для несгруппированных данных
для сгруппированных
данных
Слайд 17
Коэффициент вариации
представляет собой выраженное в процентах отношение
среднего квадратического отклонения к средней арифметической:
Коэффициент вариации используют как
характеристику однородности совокупности.
Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.