Слайд 2
Основные определения
Генеральной совокупностью называется совокупность однородных (относительно некоторого
признака) объектов, на которой ставится статистическая задача
Выборочной совокупностью (выборкой)
называется совокупность случайно отобранных предметов из генеральной совокупности. Совокупность объектов, на которой решается статистическая задача
Объемом совокупности (выборочной или генеральной) называется число объектов этой совокупности (n<
Слайд 3
Виды выборок
Определение. Выборки называются независимыми (несвязными), если процедура
эксперимента и полученные результаты измерения некоторого свойства у испытуемых
одной выборки не оказывают влияния на особенности протекания этого же эксперимента и результаты измерения этого же свойства у испытуемых (респондентов) другой выборки.
Слайд 4
Виды выборок
Определение. Выборки называется зависимыми (связными) если процедура
эксперимента и полученные результаты измерения некоторого свойства, проведенные на
одной выборке, оказывают влияние на другую.
Одна и та же группа испытуемых, на которой дважды проводилось обследование (пусть даже разных качеств, признаков, особенностей), по определению оказывается зависимой, или связной выборкой.
Слайд 5
ШКАЛЫ
1. Номинальная шкала
(шкала наименований)
- делит все
объекты на группы по какому-либо признаку (различию).
Примеры шкалы наименований:
пол, национальность, семейное положение, образование, здоровый – больной, левша – правша, тип темперамента, тип личности и т.п.
Слайд 6
2. Шкала порядка (порядковая, ранговая, ординальная)
предназначена для
измерения (обозначения) степени различия какого-либо признака или свойства у
разных объектов.
Пример.
Слайд 7
Разновидности порядкового шкалирования (измерения):
ранжирование (в ряд),
группировка (ранжирование
по группам),
парное сравнение,
метод рейтинга,
метод полярных профилей.
Слайд 8
3. Интервальная шкала (интервальное измерение)
– это такое
присвоение чисел объектам, когда определено расстояние между объектами и
предусмотрена общая для всех объектов постоянная единица измерения. Иначе говоря, в интервальной шкале вводится единица и масштаб измерения. Нулевая точка шкалы выбирается произвольно.
Пример.
Слайд 9
4. Шкала отношений (пропорциональная шкала)
- отличается от
интервальной только тем, что ее нулевая точка не произвольна,
а указывает на полное отсутствие измеряемого свойства.
Примеры пропорциональных шкал: расстояние, длина отрезков или физических объектов, время, температура по Кельвину (абсолютный нуль).
Возможны все арифметические действия.
Слайд 10
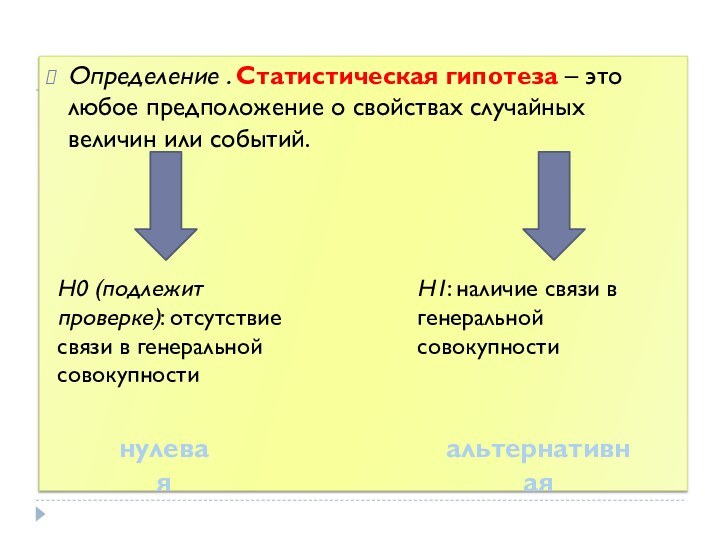
Определение . Статистическая гипотеза – это любое предположение
о свойствах случайных величин или событий.
Н0 (подлежит проверке):
отсутствие связи в генеральной совокупности
Н1: наличие связи в генеральной совокупности
нулевая
альтернативная
Слайд 11
?! Какие выборки, какие измерения?
1. Уровень статистической значимости
Определение.
Статистическая значимость (р-уровень значимости) – количественная оценка надежности установленной
связи.
Чем меньше значение р-уровня, тем выше статистическая значимость результата исследования, который подтверждает научную гипотезу
!
Проверка статистических гипотез
Слайд 12
Определение . Статистический критерий – это инструмент для
определения уровня статистической значимости гипотезы
Определение. Число степеней свободы
– это количество возможных направлений изменчивости признака.
Зависит от:
объема выборки,
от числа изучаемых признаков
Определение. Назначение критерия – проверка статистической гипотезы путем определения р-уровня значимости
2. Статистический критерий и число степеней свободы
Слайд 13
Структура статистического критерия
формула расчета наблюдаемого (эмпирического) значения критерия
по выборочным статистикам;
правило определения числа степеней свободы;
критическое значение критерия
для данного числа степеней свободы;
правило соотнесения наблюдаемого значения критерия с критическим для определения вероятности того, что Н0 верна.
Слайд 14
Алгоритм проверки гипотезы
Выбор критерия в зависимости от
вида исходных данных и статистической гипотезы
Расчет по исходным данным
(или по имеющимся статистикам) наблюдаемого (эмпирического) значения критерия и числа степеней свободы
Применение «Таблицы критических значений критерия» позволяет определить значение р-уровня для данного числа степеней свободы
Слайд 15
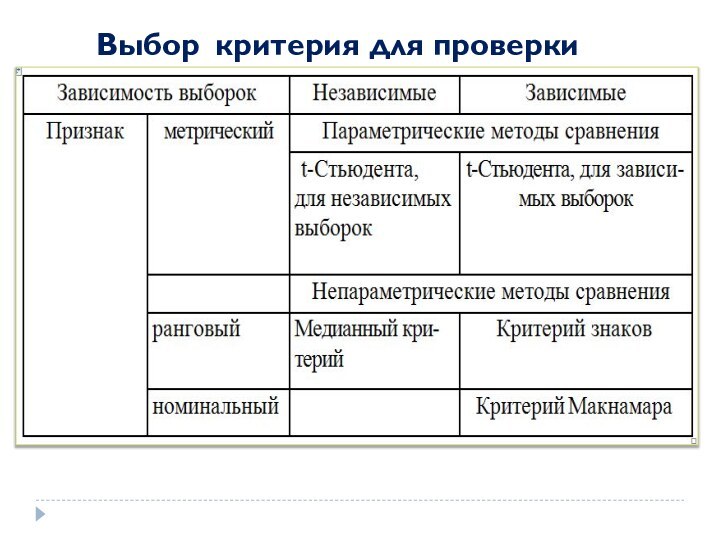
Выбор метода статистической проверки гипотезы
Определяется:
типом используемой шкалы
количеством сравниваемых
групп
зависимостью или независимостью сравниваемых выборок
Слайд 16
Классификация критериев
Непараметрические критерии статистики: закон распределения выборок не
известен , наблюдения независимые
Параметрические критерии : вид распределения или
функция распределения выборки нам заданы
Слайд 18
Параметрические критерии
Критерий Стьюдента
! Распределение выборок – нормальное
Случай
независимых выборок
n1 - число элементов в первой выборке
n2
- число элементов во второй выборке
Статистика критерия:
- средние арифметические в экспериментальной и контрольной группах
число степеней свободы: k = n1 + n2 – 2
Слайд 19
Принятие решения:
1. Сравнить полученное значение tэмп с критическим
значением t-распределения Стьюдента (приложение 1).
2. Если tэмп
гипотеза H0 принимается, в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза.
Пример:
Сформулировать нулевую и альтернативную гипотезы и проверить, какая верна
Слайд 20
Случай связанных (парных) выборок
Число степеней свободы k
= n-1
Принятие решения. Если tэмп
в противном случае принимается альтернативная.
Статистика критерия:
1. Вычислим:
2. Вычислим:
3. Вычислим:
Слайд 21
Пример.
Данные тестирования до и после начала эксперимента. Сформулировать
нулевую и альтернативную гипотезы и проверить, какая из них
принимается
Слайд 22
Непараметрические критерии
Критерий Макнамары
!!! Условия:
выборки зависимые;
для получения данных
использовалась шкала наименований;
выборки случайные;
результаты измерений интересующего свойства не влияют
друг на друга.
Х - состояние некоторого свойства в рассматриваемой совокупности объектов при первичном измерении свойства.
Y –при вторичном измерении.
– до применения средства;
– после применения средства.
Слайд 24
Статистика критерия и принятие решения:
Если n=b+c> 20, то
tэмп =
Если tэмп
и альтернативная гипотеза отклоняется.
Если n=b+c ≤ 20, то вычисляем T2= min (b,c). По n и T2 находим tэмп по таблице на стр. 111 и сопоставляем это значение с t кр.= 0.025.
Если tэмп < Ткр., то нулевая гипотеза отклоняется.
а) Если bб) Если b>c, то принимается гипотеза Н1: P( xi=0, yi=1)>P(xi=1, yi=0).
Слайд 25
Пример 1.
Проверка эффективности форм адаптационной работы среди учащихся
первых классов. Эффективность каждого цикла работы выяснялась по отношению
учащихся к обучению (ответы: да, нравится/ нет, не нравится). Из 150 человек отобрана выборка – 20 учащихся. Используется критерий Макнамары.
Задание: сформулировать гипотезы и проверить, какая принимается
Слайд 26
Пример 2.
В эксперименте 100 испытуемых. Проверяется наличие (отсутствие)
качества в ходе двух последовательных срезов, между которыми -
работа по формированию этого качества.
Задание: сформулировать гипотезы и проверить, какая принимается
Слайд 27
Критерий знаков (G-критерий)
Условия:
зависимые выборки
шкала не ниже
ранговой
Наблюдения над случайными переменными X и У, полученные при
рассмотрении двух зависимых выборок
Н0: в состоянии изучаемого свойства нет значимых различий при первичном и вторичном измерениях
Н1: законы распределения величин X и У различны
Слайд 28
Статистика критерия: tэмп – количество пар со знаком
плюс, n= количество пар без нулей
! Нулевая гипотеза принимается
на уровне значимости 0,025, если tэмп
Пример: новый метод, два среза
Задание: сформулировать гипотезы и проверить, какая принимается
Слайд 29
Медианный критерий
Условия:
выборки независимые;
выборки случайные;
шкала измерений не менее порядковой;
Совокупный
объем выборок не менее 40.
– состояния изучаемого свойства в первой совокупности; – состояния изучаемого свойства во второй совокупности.
N1- объем первой выборки; N2- объем второй выборки;
MeX – медиана совместной выборки.
Слайд 30
Систематизация:
Важно! Критерий можно применять, если A,B,C,D≥ 5.
H0: обе
совокупности имеют одинаковую медиану (нет значимых различий между выборками);
H1:
совокупности имеют различные медианы (существуют значимые различия между выборками).
Слайд 31
Статистика критерия:
Принятие решения: H0 принимается, если
tэмп
наблюдается достаточно большое количество значений выборок вблизи медианы, то
следует использовать уточненное значение медианы.
tэмп