Слайд 2
1.ПРЕДМЕТ И МЕТОД СТАТИСТИКИ
Статистика имеет многовековую историю.

Её возникновение и развитие обусловлены общественными потребностями: подсчет населения,
скота, учета земельных угодий, имущества и т.д. Наиболее ранние сведения о таких работах в Китае относятся к 13в. до нашей эры. В Древнем Риме проводились учеты свободных граждан и их имущества.
Считается, что основы статистической науки заложены английским экономистом У. Петти (1623-1687)г., который рассматривал статистику как науку об управлении. В 1746г. немецкий профессор философии и права Ахенваль впервые в Марбургском университете начал читать новую дисциплину, названную им статистикой.
В развитии статистики видное место принадлежит представителям отечественной науки и практики. В эпоху Петра I статистика трактовалась преимущественно как описательная наука. Но уже со второй половины XIX в. выдвигается познавательное значение статистики. Профессор петербургского университета Ю.Э. Янсон (1835-93) назвал статистику общественной наукой. Видный экономист А.И. Чупров (1842-1908) отмечал необходимость массового статистического исследования при помощи метода количественного наблюдения большого числа факторов для того, чтобы описать общественные явления, подметить законы и определить причины, их вызвавшие. Развитие статистики в России тесным образом связано с созданной после отмены крепостного права земской статистикой, которая пользовалась заслуженным авторитетом за объективность и профессионализм.
Слайд 3
В настоящее время статистика имеет следующее определение: статистика

- это планомерный и систематический учет массовых общественных явлений,
который осуществляется государственными статистическими органами и дает числовое выражение проявляющимся закономерностям.
Направлений в статистике очень много, например: статистика промышленности, статистика торговли, экономическая статистика, математическая, прикладная и т.д.
Поскольку статистика имеет дело с массовыми явлениями, то основным понятием является статистическая совокупность.
Статистическая совокупность - это множество объектов или явлений, изучаемых статистикой, которые имеют один или несколько общих признаков и различаются между собой по другим признакам. Так, например, при определении объема розничного товарооборота все предприятия торговли, осуществляющие продажу товаров населению, рассматриваются как единая статистическая совокупность — "розничная торговля".
Отдельные объекты или явления, образующие статистическую совокупность, называются единицами совокупности.
Например, при проведении переписи торгового оборудования единицей наблюдения является торговое предприятие, а единицей совокупности - их оборудование (прилавки, холодильные агрегаты и т.д.).
Явления и процессы в жизни общества изучаются статистикой посредством статистических показателей.
Статистический показатель - это количественная оценка свойства изучаемого явления.
Слайд 4
Одной из важных категорий статистической науки является понятие

признака.
Признак - это характерное свойство изучаемого явления, отличающее его
от других явлений.
В разных отраслях статистики изучаются разные признаки. Так, например, объектом изучения является предприятие, а его признаками - вид продукции, объем выпуска, число работающих и т.д. Или, например, объект - отдельный человек, а признаки - пол, возраст, национальность, рост, вес и т.д.
Таким образом, статистических признаков, т.е. свойств, качеств объектов наблюдения очень много. Все их многообразие принято делить на две большие группы: признаки качества и признаки количества.
Признак
Качественный признак (атрибутивный) - признак, отдельные значения которого выражаются в виде понятий, наименований. Например, профессия — токарь, слесарь, технолог, учитель, врач и т.д.
Количественный признак - признак, определенные значения которого имеют количественные выражения.
Например:
Рост - 185, 172, 164, 158.
Вес - 105, 72, 54, 48.
Каждый объект изучения может обладать целым рядом статистических признаков, но от объекта к объекту одни признаки меняются, другие остаются неизменными. Вариация - это многообразие, изменяемость величины признака у отдельных единиц совокупности наблюдения.
Вариация признака - пол - мужской, женский.
Вариация з/п - 10000, 100000, 1000000.
Слайд 5
Статистическое наблюдение
Статистическое наблюдение — это начальная стадия экономико-статистического

наблюдения, научно организационная работа по собиранию массовых первичных данных
о явлениях и процессах общественной жизни. Любое статистическое наблюдение осуществляется с помощью оценки и регистрации признаков единиц совокупности в соответствующих учетных документах. Таким образом, полученные данные представляют собой факты, которые так или иначе характеризуют явления общественной жизни.
Статистическое наблюдение должно отвечать следующим требованиям.
1. Наблюдаемые явления должны иметь научную и практическую ценность, выражать определенные социально-экономические типы явлений.
2. Непосредственный сбор массовых данных должен обеспечить полноту фактов, относящихся к рассматриваемому вопросу, так как явления находятся в постоянном изменении, развитии. В том случае, если отсутствуют полные данные, анализ и выводы могут быть ошибочными.
3. Для обеспечения достоверности статистических данных необходима тщательная всесторонняя проверка (контроль) качества собираемых фактов.
4. Для того, чтобы создать наилучшие условия для получения объективных материалов, необходима научная организация статистического наблюдения.
Статистическое наблюдение осуществляется в двух формах: путём предоставления отчётности и проведения специально организованных статистических наблюдений.
Отчётностью называют такую организованную форму статистического наблюдения, при которой сведения поступают в виде обязательных отчётов в определённые сроки и по утверждённым формам.
Слайд 6
Специально организованное статистическое наблюдение представляет собой сбор сведений

посредством переписей, единовременных учётов и обследований.
Виды статистического наблюдения
различаются по времени регистрации данных и по степени охвата единиц исследуемой совокупности.По характеру регистрации данных во времени различают наблюдение непрерывное, или текущее, и прерывное (периодическое). Последнее, в свою очередь подразделяется на наблюдение периодическое и наблюдение единовременное.
Текущим (непрерывным) является такое наблюдение, которое ведётся систематически. При этом регистрация фактов производится по мере их свершения, например, регистрация актов гражданского состояния, учёт произведённой продукции, отпуска материалов со склада, выручки магазинов. При текущем наблюдении нельзя допускать значительного разрыва между моментом возникновения факта и моментом его регистрации.
Прерывным (периодическим) является такое наблюдение, которое повторяется через определённые промежутки времени. Например, ежегодные переписи скота, проводимые по состоянию на 1 января.
Единовременное (разовое) наблюдение проводится по мере надобности, время от времени, без соблюдения строгой периодичности или вообще проводится единожды. Примером могут служить социально-экономические выборочные обследования, проводимые Научно-исследовательским институтом по изучению спроса на товары народного потребления и конъюнктуры торговли.
По степени охвата единиц изучаемой совокупности различают сплошные и несплошные статистические наблюдения.
Сплошным называют такое наблюдение, при котором обследованию подвергаются все без исключения единицы изучаемой совокупности. Примером сплошного наблюдения может служить Всесоюзная перепись населения. Путем сплошного наблюдения осуществляется получение отчетности от предприятий и учреждений.
Несплошным называют такое наблюдение, при котором обследованию подвергаются не все единицы изучаемой совокупности, а только заранее установленная их часть, например, изучение торговых оборотов и цен на городских рынках. Основным видом несплошного наблюдения является выборочное.
Выборочным наблюдением называется наблюдение, при котором характеристика всей совокупности фактов дается по некоторой их части, отобранной в случайном порядке. В промышленности его используют для контроля качества продукции, в сельском хозяйстве — при выявлении продуктивности скота, в контрольных проверках — при переписи скота и других работах.
Слайд 7
Ошибки статистического наблюдения.
Всякое статистическое наблюдение ставит задачу получения
таких данных, которые точнее бы отражали действительность. Отклонения, или
разности между исчисленными показателями и действительными (истинными) величинами исследуемых явлений нашли отражение в показателях, называемых ошибками, или погрешностями. В зависимости от характера и степени влияния на конечные результаты наблюдения, а также исходя из источников и причин возникновения неточностей, допускаемых в процессе статистического наблюдения, обычно выделяют ошибки регистрации и ошибки репрезентативности.
Ошибки регистрации возникают вследствие неправильного установления фактов в процессе наблюдения или неправильной их записи. Они подразделяются на случайные и систематические и могут быть как при сплошном, так и несплошном наблюдении.
Слайд 8
Ошибки регистрации
Случайные ошибки — ошибки регистрации, которые могут
быть допущены как опрашиваемыми в их ответах, так и
регистраторами при заполнении бланков.
Систематические ошибки могут быть преднамеренными, так и непреднамеренными. Преднамеренные ошибки получаются в результате того, что опрашиваемый, зная действительное положение дела, сознательно сообщает неправильные данные. Непреднамеренные ошибки вызываются различными случайными причинами (небрежностью или невнимательностью регистратора, неисправностью измерительных приборов и т.д.).
Слайд 9
Ошибки репрезентативности возникают в результате того, что состав
отобранной для обследования части единиц совокупности недостаточно полно отображает
состав всей изучаемой совокупности, хотя регистрация сведений по каждой отобранной для обследования единице была проведена точно. Ошибки репрезентативности могут быть случайными и систематическими.
Случайные ошибки возникают из-за того, что совокупность отобранных единиц наблюдения неполно воспроизводит всю совокупность в целом.
Систематические ошибки возникают вследствие нарушения принципов случайного отбора единиц изучаемой совокупности.
Слайд 10
Для выявления и устранения допущенных при регистрации ошибок
может применяться счётный и логический контроль собранного материала.
Счётный
контроль заключается в проверке точности арифметических расчётов, применявшихся при составлении отчётности или заполнении формуляров обследования.
Логический контроль заключается в проверке ответов на вопросы программы наблюдения путём их логического осмысления или путём сравнения полученных данных с другими источниками по этому вопросу.
Указанные приемы проверки статистических данных путем счетного и логического контроля могут быть использованы при проверке, как материалов специальных статистических наблюдений, так и отчетности.
Слайд 11
Статистическая отчетность.
Статистическая отчетность — это официальный документ, в

котором содержатся сведения о работе подотчетного объекта, занесенные на
специальную форму. Статистическая отчетность чаще всего базируется на данных бухгалтерского учета.
Первичный учет представляет собой регистрацию различных фактов (событий, процессов и т.д.), производимых по мере их свершения и, как правило, на первичном учетном документе. Примером может служить свидетельство о рождении ребенка. В торговле к первичным учетным документам относятся наряды на отпуск товаров, счета-фактуры, накладные и т.д. В функции первичного учета входят операции наблюдения, т.е. регистрация данных и подсчет итогов.
По своему содержанию формы отчетности бывают типовыми (общими) и специализированными.
Общая отчетность — это отчетность, содержащая одни и те же данные для определенной отрасли народного хозяйства и для предприятий (учреждений) всего народного хозяйства.
В специализированной отчетности содержатся специфические показатели отдельных отраслей промышленности, сельского хозяйства и т.п.
По периоду времени, за который предоставляется отчетность, по его длительности различают отчетность текущую и годовую. Если сведения представляются за год, то такую отчетность называют годовой. Отчетность за все другие периоды в пределах менее года, соответственно квартальная, месячная, недельная и т.п. называется текущей
Слайд 12
Обобщающие статистические показатели.
Обобщающие статистические показатели отражают количественную сторону

изучаемой совокупности общественных явлений, представляют собой их величину, выраженную
соответствующей единицей измерения.
Практически статистическая информация начинает формироваться с абсолютных величин, ими измеряются все стороны общественной жизни.
Абсолютные величины, выражающие размеры (уровни, объемы) явлений и процессов, получают в результате статистического наблюдения и сводки исходной информации, это всегда числа именованные, имеющие определенную размерность, единицы измерения. В зависимости от различных причин и целей анализа применяются натуральные, денежные (стоимостные) и трудовые единицы измерения.
По способу выражения размеров изучаемых явлений абсолютные величины подразделяются на индивидуальные и суммарные, которые представляют собой один из видов обобщающих величин.
Индивидуальные — характеризуют размеры количественных признаков у отдельных единиц. Этот вид показателей служит основанием при статистической сводке для включения единиц объекта в группы. На их базе получают абсолютные величины, из которых, в свою очередь, можно выделить показатели численности совокупности и показатели объема признаков совокупности.
Изучая экономические явления, статистика не может ограничиваться исчислением только абсолютных величин, в анализе статистической информации важное место занимают производные обобщающие показатели — средние и относительные величины.
Относительные величины в статистике представляют собой частное от деления двух статистических величин и характеризуют количественное соотношение между ними.
При расчете относительных величин следует иметь в виду, что в числителе всегда находится показатель, отражающий то явление, которое изучается, т.е. сравниваемый показатель, а в знаменателе — показатель, с которым производится сравнение, принимаемый за основание или базу сравнения. База сравнения выступает в качестве своеобразного измерителя. В зависимости от того, какое числовое значение имеет база сравнения, результат отношения может быть выражен либо в форме коэффициента и процента, либо в форме промилле и децимилле.
Если значение основания или базы сравнения принимается за единицу, то относительная величина является коэффициентом и показывает, во сколько раз изучаемая величина больше основания.
Слайд 13
Способы определения относительных величин.
Пример 1.
Из общей численности населения

России, равной на конец 1985г. 143,8 млн. человек, 104,1
млн. составляли городские жители, 39,7 млн. — сельские. Рассчитав относительные величины структуры, можно определить удельные веса (или доли городских и сельских жителей) в общей численности населения страны, т.е. структуру населения по месту жительства:
городское — (104,1 / 143,8) *100 = 72,4:
сельское — (39,7 / 143,8) *100 = 27,6.
Спустя 6 лет, численность населения страны составила 148,7 млн., в том числе: городских жителей — 109,7 млн., сельских — 39,0 млн. Исходя из этих данных исчисляются показатели структуры населения:
городское — (109,7 / 148,7) *100 = 73,8:
сельское — (39,0 / 148,7) *100 = 26,2.
Сравнив состав населения страны в 1985г. и 1991г., можно сделать вывод о том, что происходит увеличение удельного веса городских жителей.
1. Относительные величины структуры характеризуют состав изучаемой совокупности. Исчисляются они как отношение абсолютной величины каждого из элементов совокупности к абсолютной величине всей совокупности, т.е. как отношение части к целому, и представляют собой удельный вес части в целом.
Как правило, относительные величины структуры выражаются в процентах (база сравнения принимается за 100) или в долях (база сравнения принимается за 1).
Слайд 14
Способы определения относительных величин.
Пример 2.
Реализация хлопчатобумажных тканей секцией
универмага составила в январе 3950 тыс. руб., в феврале
— 4200 тыс. руб., в марте — 4700 тыс. руб.
Темпы роста:
базисные (база — уровень реализации в январе)
= 4200:3950*100 = 106,3%
= 4700:3950*100 = 118,9%
цепные
= 4200:3950*100 = 106,3%
= 4700:4200*100 = 111,9%
2. Относительные величины динамики характеризуют изменение изучаемого явления во времени, выявляют направление развития, измеряют интенсивность развития. Расчет относительных величин выполняется в виде темпов роста и других показателей динамики.
Слайд 15
Способы определения относительных величин.
Пример 3.
По данным Всесоюзной переписи
населения 1989г. численность населения Москвы составила 8967 тыс., а
численность населения Санкт-Петербурга — 5020 тыс. человек.
Рассчитаем относительную величину сравнения, приняв за базу сравнения численность жителей Санкт-Петербурга: 8967 / 5020 = 1,79. Следовательно, численность населения Москвы в 1,79 раза больше, чем в Санкт-Петербурге.
3. Относительные величины сравнения характеризуют количественное соотношение одноименных показателей, относящихся к различным объектам статистического наблюдения.
Слайд 16
Способы определения относительных величин.
Пример 4.
На начало года численность
специалистов с высшим образованием, занятых в ассоциации “Торговый дом”,
составила 53 человека, а численность специалистов со средним специальным образованием — 106 человек. Приняв за базу сравнения численность специалистов с высшим образованием, рассчитаем относительную величину координации: 106/53=2,0/1,0, т.е. на двух специалистов со средним специальным образованием приходится один специалист с высшим образованием.
4. Относительные величины координации применяются для характеристики соотношения между отдельными частями статистической совокупности и показывают, во сколько раз сравниваемая часть совокупности больше или меньше части, которая принимается за основание или базу сравнения.
Слайд 17
Способы определения относительных величин.
Пример 5.
Число предприятий розничной торговли
региона на конец года составило 6324. Численность населения данного
региона на ту же дату составила 234,2 тыс. человек. Следовательно, на каждые 10000 человек в данном регионе приходится 27,3 предприятия розничной торговли: [(6324*10000):234200]=27,3 предприятия.
5. Относительные величины интенсивности показывают, насколько широко распространено изучаемое явление в той или иной среде, т.е. сколько единиц одной совокупности приходится на единицу другой совокупности.
Слайд 18
2.МЕТОД ГРУППИРОВКИ
Группировка статистических данных
В результате первой стадии
статистического исследования (статистического наблюдения) получают сведения о каждой единице
совокупности. Задача второй стадии статистического исследования состоит в том, чтобы упорядочить и обобщить первичный материал, свести его в группы и на этой основе дать обобщающую характеристику совокупности. Этот этап в статистике называется сводкой.
Различают простую сводку (подсчет только общих итогов) и статистическую группировку, которая сводится к расчленению совокупности на группы по существенному для единиц совокупности признаку. Группировка позволяет получить такие результаты, по которым можно выявить состав совокупности, характерные черты и свойства типичных явлений, обнаружить закономерности и взаимосвязи.
Результаты сводки могут быть представлены в виде статистических рядов распределения.
Слайд 19
Статистическим рядом распределения называют упорядоченное распределение единиц совокупности
на группы по изучаемому признаку. В зависимости от признака
ряды могут быть вариационными (количественными) и атрибутивными (качественными).
Ряды
Количественные признаки — это признаки, имеющие количественное выражение у отдельных единиц совокупности, например, заработная плата рабочих, стоимость продукции промышленных предприятий, возраст людей, урожайность отдельных участков посевной площади и т.д.
Вариационные ряды могут быть дискретными или интервальными.
Дискретный ряд распределения — это ряд, в котором варианты выражены целым числом.
Интервальный ряд распределения — это ряд, в котором значения признака заданы в виде интервала.
Атрибутивные признаки — это признаки, не имеющие количественной меры. Например, пол (мужской, женский), отрасль народного хозяйства, вид продукции, профессия рабочего и т.д.
Слайд 20
Статистические ряды распределения позволяют систематизировать и обобщать статистический

материал. Однако они не дают всесторонней характеристики выделенных групп.
Чтобы решить ряд конкретных задач, выявить особенности в развитии явления, обнаружить тенденции, установить зависимости, необходимо произвести группировку статистических данных.
Группировка - это процесс образования групп единиц совокупности однородных в каком-либо отношении, а также имеющих одинаковые или близкие значения группировочного признака.
Чтобы решить ряд конкретных задач, выявить особенности в развитии явлений, обнаружить тенденции, установить зависимости, необходимо произвести группировку статистических данных.
Для этой цели выбирается группировочный признак и разрабатывается система показателей, которыми будут характеризоваться выделенные группы. Определение и обоснование показателей целиком зависят от цели исследования и поставленной задачи. В зависимости от цели и задач исследования различают следующие виды группировок: типологические, структурные, аналитические.
Слайд 21
К типологическим группировкам относят все группировки, которые характеризуют
качественные особенности и различия между типами явлений.
Типологические группировки
широко применяются в экономических, социальных и других исследованиях.
Распределение промышленной продукции, произведенной в различных формах хозяйствования за отчетный период.
Из таблицы видно, что происходят изменения в социальной занятости работников в народном хозяйстве: увеличилось число работников в кооперативном и индивидуальном секторах экономики.
Пример типологической группировки
Слайд 22
Структурная группировка - это группировка, выявляющая состав (строение,
структуру) однородной в качественном отношении совокупности по какому-либо признаку.
Примером могут служить группировки предприятий по проценту выполнения плана, по числу рабочих и т.д. Состав населения может быть сгруппирован по полу, по возрасту, по уровню образования, по роду занятий и т.д. Значение такого рода группировок заключается в том, что с их помощью могут быть выделены и изучены группы предприятий передовых, средних, отстающих; выявлены неиспользованные резервы производства, Группировка населения по возрасту, например, необходима для проведения различных расчетов, связанных с медицинским, культурным, бытовым обслуживанием населения, для вычисления специальных демографических показателей и т.д.
Из данной группировки можно сделать следующий вывод - наибольшая численность рабочих приходится на группу заводов со среднегодовой стоимостью ОПФ от 2,2 до 3,4 млн. руб.
Пример структурной группировки
Слайд 23
Аналитическая группировка - это группировка, которая применяется для
исследования взаимосвязи между явлениями. Используя аналитические группировки, определяют факторные
и результативные признаки изучаемых явлений.
Факторные - это признаки, оказывающие влияние на другие, связанные с ними признаки.
Результативные – это признаки, которые изменяются под влиянием факторных.
Вывод по группировке: чем больше торговая площадь (факторный признак), тем выше объем товарооборота (результативный признак).
Пример аналитической группировки
Слайд 24
Образование групп по двум и более признакам, взятым

в определенном сочетании, называется комбинированной группировкой. При этом группировочные
признаки принято располагать, начиная с атрибутивного, в определенной последовательности, исходя из логики взаимосвязи показателей.
Техника проведения группировки.
Для построения группировки статистических данных необходимо: 1)выделить группировочный признак или основание группировки, 2)необходимо определить число интервалов группировки и их границы.
Группировочный признак при анализе выбирается из условия выполнения цели группировки.
Так, если есть статистические данные о промышленных предприятиях отрасли, то можно в качестве группировочного признака выбрать такие величины: число рабочих на предприятии; число всех работающих; мощность энергоустановок; объем выпуска продукции; стоимость ОПФ и т.д.
Таким образом, по каждому из этих признаков, множество предприятий отрасли можно разбить на группы.
Интервалы группировки могут равные и неравные. Равные интервалы используются, когда изменение признака внутри совокупности происходит равномерно, либо если далее планируется последующая математическая обработка сгруппированных данных. Неравные интервалы обычно используются как прогрессивно увеличивающиеся. В экономической статистике чаще всего устанавливаются границы интервалов, основанные именно на таком принципе - прогрессивно увеличивающиеся.
Число групп в группировке выбирается в этом случае из таких предпосылок: изменчивость признака, число наблюдений, однородность групп.
Слайд 25
Пример формирования группировки.
Пусть имеются данные о работе 24
заводов одной из отраслей промышленности (табл.).
В качестве изучаемого признака
возьмем стоимость основных производственных фондов (ОПФ) и построим к нему ряд распределения с равными закрытыми интервалами. Величина интервала определяется по формуле:
,где
и
максимальное и минимальное значения стоимости основных фондов, n - число групп.
Слайд 26
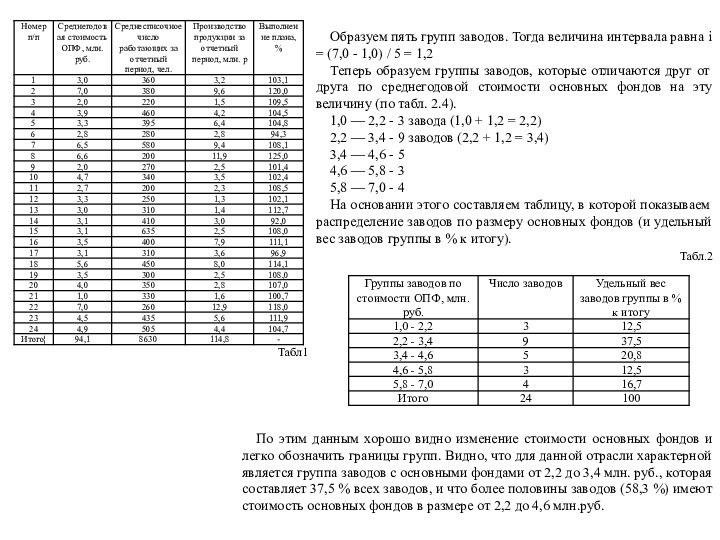
Образуем пять групп заводов. Тогда величина интервала равна
i = (7,0 - 1,0) / 5 = 1,2
Теперь
образуем группы заводов, которые отличаются друг от друга по среднегодовой стоимости основных фондов на эту величину (по табл. 2.4).
1,0 — 2,2 - 3 завода (1,0 + 1,2 = 2,2)
2,2 — 3,4 - 9 заводов (2,2 + 1,2 = 3,4)
3,4 — 4,6 - 5
4,6 — 5,8 - 3
5,8 — 7,0 - 4
На основании этого составляем таблицу, в которой показываем распределение заводов по размеру основных фондов (и удельный вес заводов группы в % к итогу).
По этим данным хорошо видно изменение стоимости основных фондов и легко обозначить границы групп. Видно, что для данной отрасли характерной является группа заводов с основными фондами от 2,2 до 3,4 млн. руб., которая составляет 37,5 % всех заводов, и что более половины заводов (58,3 %) имеют стоимость основных фондов в размере от 2,2 до 4,6 млн.руб.
Табл.2
Табл1
Слайд 27
Теперь перейдем непосредственно к методу группировки. Для этого

необходимо выбрать группировочный признак. Выявим данной отрасли промышленности распределение
предприятий по мощности, а также влияние этого признака на объем производства. Мощность предприятия в значительной степени определяется размером основных фондов (здания, сооружение, машины, оборудование).
Чтобы выявить распределение предприятий по мощности, необходимо разбить совокупность заводов отрасли на группы по размеру стоимости основных фондов. Выше мы рассматривали построения рядов распределения, были выявлены пять групп.
Составим таблицу с системой показателей, куда занесем результаты группировки заводов по среднегодовой стоимости основных производственных фондов
Таким образом, в отличие от ряда распределения (табл. 2.) группировка позволяет сделать конкретные и содержательные выводы. Данная группировка показывает, что наиболее крупные предприятия имеют лучшие производственные показатели. Около 29 % предприятий (группы 4 и 5) имеют 45% всех основных фондов и дают 52% всего объема промышленной продукции, имея лишь 31% общего числа рабочих.
Слайд 28
Приемы вторичной группировки.
Перегруппировка ранее сгруппированных статистических данных называется
вторичной группировкой. К этому методу прибегают в тех случаях,
когда в результате первоначальной группировки нечетко проявился характер распределения изучаемой совокупности.
В этом случае производят укрупнение или уменьшение интервалов. Также вторичная группировка используется для приведения к сопоставимому виду группировок с различными интервалами с целью их сравнения. Рассмотрим приемы вторичной группировки на примере.
Слайд 29
Пример 6.
Произвести укрупнение интервалов на основе данных таблицы
4.:
Приведенная группировка недостаточно наглядна, потому что не показывает четкой
и строгой закономерности в изменении товарооборота по группам.
Уплотним ряды распределения, образовав шесть групп. Новые группы образованы путем суммирования первоначальных групп (табл 5.).
Из таблицы четко видно, что чем крупнее магазины, тем выше уровень товарооборота.
Табл.5
Слайд 30
3.ВИЗУАЛИЗАЦИЯ СТАТИСТИЧЕСКИХ ДАННЫХ
Статистические таблицы
Статистические таблицы - это наиболее

рациональная форма представления результатов статистической сводки и группировки. Значение
статистических таблиц состоит в том, что они позволяют охватить материалы статистической сводки в целом. Статистическая таблица, по существу, является системой мыслей об исследуемом объекте, излагаемых цифрами на основе определенного порядка в расположении систематизированной информации.
В экономической и управленческой работе, связанной с коммерческой деятельностью, статистические таблицы применяются очень часто.
По внешнему виду статистическая таблица представляет собой ряд пересекающихся горизонтальных и вертикальных линий, образующих по горизонтали строки, а по вертикали - графы (столбцы, колонки), которые в совокупности составляют как бы скелет таблицы.
Таблица, состоящая из строк и граф, которые еще не заполнены цифрами, называется макетом таблицы. Каждая статистическая таблица имеет подлежащее и сказуемое.
Подлежащее таблицы - это объект нашего изучения (название района, города, предприятия).
Сказуемое - это система показателей, которыми характеризуется объект изучения, т.е. подлежащее таблицы.
Обычно подлежащее располагается слева, в виде наименования горизонтальных строк, а сказуемое - справа, в виде наименования вертикальных граф.
Обязательная часть таблицы - заголовок, показывающий, о чем идет речь в таблице, к какому месту и времени
она относится.
Слайд 31
В зависимости от построения подлежащего, таблицы делятся на
три вида: простые, групповые и комбинационные.
Простые таблицы получили большое
распространение во многих экономических разработках.
Простыми таблицами называются такие, в подлежащем которых нет группировок, а дается лишь перечень единиц совокупности (перечневые таблицы), административных районов (территориальные таблицы) или периодов времени (хронологические таблицы).
Рассмотрим пример простой таблицы, в подлежащем которого содержатся перечисления единиц изучаемой совокупности (табл. 3.1).
Продажа продуктов питания
продовольственными магазинами города
Наличие таких данных имеет важное информативное значение.
Сведения о простой таблице применяют для оценки измерения какого - либо явления во времени. Для этого в
подлежащем таблицы приводятся периоды времени или даты, а в сказуемом - ряд показателей.
Слайд 32
Хронологическую таблицу можно составлять за любые по величине
отрезки времени или на моменты, отстоящие друг от друга
по времени на различную длину.
Таблицы, в подлежащем которых приводится перечень территорий (районов, областей и т.п.), называются перечневыми территориальными.
Довольно часто применяются и территориально-хронологические таблицы, в которых сказуемое также содержит показатели по годам, кварталам и т.д., а подлежащее - показатели по районам, областям (табл. 3.2).
Наличие такого сочетания в построении простых таблиц усиливает их информационные возможности, и все же этот вид таблиц в основном носит описательный характер.
Процент женщин в общей численности
рабочих и служащих
Слайд 33
Групповые статистические таблицы дают более информативный материал для

анализа изучаемых явлений, благодаря образованным в их подлежащем группам
по существенному признаку или выявлению связи между рядом показателей.
Комбинационными таблицами называются такие, в которых подлежащее содержит группировку единиц совокупности по двум или более признакам, взятым в сочетании. Комбинационная таблица устанавливает взаимное действие на результативные признаки существующую связь между факторами группировки.
При составлении таблицы надо соблюдать ряд правил:
четко формулировать наименование, которое должно точно отражать цель составления таблицы;
ясно и кратко формулировать название строк и граф таблицы;
соблюдать последовательность расположения показателей сказуемого;
указывать единицы измерения; если они одинаковые, то ед. измерения выносятся в заголовок и указываются в
скобках;
нумеровать графы;
иметь итоговые показатели;
если в таблице производится сопоставление с каким-либо годом, то в заголовке, в скобках, отражается год
сопоставления;
территориальные, административные образования перечисляются по алфавиту;
данные за многие годы располагаются в хронологическом порядке;
если в таблице абсолютные и относительные показатели за ряд лет, то сначала приводятся абсолютные, затем
относительные показатели за один год, затем так же за следующий год;
если значение признака в какой-либо клетке неизвестно, ставится знак Х, или ... , или н. с. (нет сведений);
нулевые значения признака - знак “—” .
Слайд 34
Пример записи статистических данных в виде таблицы.
Задача. Численность

населения РСФСР по переписи населения 1959 г. составляла 117,5
млн. человек, в том числе городского — 61,6 млн. человек, сельского — 55,9 млн. человек, что ко всему населению соответственно равно 52 и 48%. По данным переписи населения 1970 г. общая численность населения республики выросла до 130,1 млн. человек, из которых на городское население приходилось — 81,0 млн. человек и на сельское — 49,1 млн. человек, или в процентах к общей численности соответственно 62 и 38. На 1 января 1979 г. было зарегистрировано всего 136,5 млн. человек, в том числе городского населения — 95,2 млн. человек и сельского — 41,3 млн. человек, что соответственно равно 70 и 30% общей численности населения.
Представим эти данные в виде таблицы. При построении таблицы наиболее целесообразно слева поместить годы, а в вертикальных графах — показатели (сначала абсолютные, затем относительные). При таком расположении, просматривая цифры в отдельных столбцах сверху вниз, можно легко проследить закономерности динамики и изменения структуры населения. Рассмотрим изменение численности городского и сельского населения РСФСР за 1959 - 1979 гг.
Благодаря определённой системе расположения данных, устраняются повторения, достигается наглядность,
удобство обозрения, краткость изложения, появляется возможность сравнения и анализа.
Слайд 35
Статистические графики
Важное значение при изучении коммерческой деятельности имеет

графическое изображение статистической информации. Правильно построенный график делает статистическую
информацию более выразительной, запоминающейся и удобно воспринимаемой.
Применение графиков в статистике насчитывает более чем двухсотлетнюю историю. Основоположником графического метода в статистике коммерческой деятельности считают английского экономиста У. Плейфейра (1731 — 1798). В своих работах он впервые применил способы графического изображения статистических данных (линейные, столбиковые, секторные и другие диаграммы).
Статистические графики - это одно из самых наглядных средств представления информации, представляет собой чертеж, на котором при помощи условных геометрических фигур изображаются статистические данные. В результате этого достигается наглядная характеристика изучаемой статистической совокупности. Правильно построенный график делает статистическую информацию более выразительной, запоминающейся и удобно воспринимаемой.
В статистическом графике различают следующие основные элементы:
поле графика;
графический образ;
пространственные и масштабные ориентиры;
экспликация графика.
Полем графика является место, на котором он выполняется. Это листы бумаги, географические карты, план местности и т.п. Поле графика характеризуется его форматом (размерами и пропорциями сторон). Размер поля графика зависит от его назначения.
Графический образ — это символические знаки, с помощью которых изображаются статистические данные (линии, точки, прямоугольники, квадраты, круги и т.д.). В качестве графического образа выступают и объемные фигуры. Иногда в графиках используются негеометрические фигуры в виде силуэтов или рисунков предметов.
Слайд 36
Пространственные ориентиры определяют размещение графических образов на поле

графика. Они задаются координатной сеткой или контурными линиями и
делят поле графика на части, соответствующие значениям изучаемых показателей.
Масштабные ориентиры статистического графика придают графическим образам количественную значимость, которая передается с помощью системы масштабных шкал.
Масштаб графика — это мера перевода численной величины в графическую (например, 1 см соответствует 100 тыс. руб.). При этом чем длиннее отрезок линии, принятой за числовую единицу, тем крупнее масштаб.
Масштабной шкалой является линия, отдельные точки которой читаются как определенные числа. Шкала, по которой отсчитываются уровни изучаемых показателей, как правило, начинается с 0. Последнее число, наносимое на шкалу, несколько превышает максимальный уровень, отсчет которого проводится по этой шкале. При построении графика допускается разрыв масштабной шкалы. Этот прием используется для изображения статистических данных, имеющих значения лишь в определенных значениях.
Экспликация графика — это пояснение его содержания, включает в себя заголовок графика, объяснения масштабных шкал, пояснения отдельных элементов графического образа.
Заголовок графика в краткой и четкой форме поясняет основное содержание изображаемых данных. Помимо заголовка, на графике дается текст, делающий возможным чтение графика. Цифровые обозначения шкалы дополняются указанием единиц измерения.
Слайд 37
Диаграмма представляет чертеж, на котором статистическая информация изображается

посредством геометрических фигур или символических знаков.
Диаграмма сравнения — показывает
соотношение признака статистической совокупности.
Рис. 1. Столбиковая диаграмма сравнения
Каждое значение изучаемого показателя изображается в виде вертикального столбика. Количество столбиков
определяется числом изучаемых показаний (данных). Расстояние между столбиками должно быть одинаковым.
У основания столбиков делается название изучаемого показателя.
Рис. 2. Полосовая диаграмма сравнения
В этих диаграммах основания столбиков располагаются вертикально. Должна быть одинаковая ширина полос.
Эту же диаграмму можем построить иначе (рис. 3.).
При построении столбиковых диаграмм используется, как и в линейных графиках, прямоугольная система
координат. По оси абсцисс размещается основание столбиков. Их ширина может быть произвольной, но
обязательно одинаковой для каждого столбика.
Рис. 3. Столбиковая диаграмма сравнения
Основные требования построения данных диаграмм:
соответствие столбиков по высоте, а полос - по длине, отображаемым цифрам;
недопустимость разрывов масштабной шкалы и начала ее не от нулевой отметки.
Слайд 38
Основные требования построения данных диаграмм:
соответствие столбиков по
высоте, а полос - по длине, отображаемым цифрам;
недопустимость
разрывов масштабной шкалы и начала ее не от нулевой отметки.
Структурная диаграмма - позволяет сопоставить статистические совокупности по составу.
Рис. 4. Структурно-столбиковая диаграмма.
Рис. 5. Структурно-секторная диаграмма
Секторная диаграмма строится таким образом, чтобы каждый сектор занимал площадь круга пропорционально
удельному весу отображаемых частей целого. Затем необходимо найти значения центральных углов
(1%=3,6 градуса).
Слайд 39
Пример построения структурно-секторной диаграммы
Определяем относительные величины структуры использования
посевных площадей колхозами.
Зерновые - 570,6/1003,1*100%=56,9%; Картофель - 27,9/1003,1*100%=2,8% и
т.д. Получаем следующие
данные (табл. 3.7).
Определяем по данным об удельных весах посевных площадей, занятых под отдельными культурами,
соответствующие значения центральных углов.
Зерновые 56,9*3,6 = 204,85
Технические 10,5*3,6 = 37,85
Картофель 2,8*3,6 = 10,15
Кормовые 29,8*3,6 = 107,35
Теперь строим секторную диаграмму, разделив круг на сектора, в соответствии с полученными значениями
центральных углов, культуры:
Рис. 6. Структура посевных площадей в колхозах области (1989г.).
Слайд 40
4.ДЕСКРИПТИВНЫЕ СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ
Средние величины.
Средние величины характеризуют качественные показатели

коммерческой деятельности: издержки обращения, прибыль, рентабельность и др.
Средняя -
это один из распространенных приемов обобщений. Правильное понимание сущности средней определяет ее особую значимость в условиях рыночной экономики, когда средняя через единичное и случайное позволяет выявить общее и необходимое, выявить тенденцию закономерностей экономического развития.
Средняя величина - это обобщающие показатели, в которых находят выражение действия общих условий, закономерностей изучаемого явления.
Каждая средняя величина характеризует изучаемую совокупность по какому-либо одному признаку. Чтобы получить полное и всестороннее представление об изучаемой совокупности по ряду существенных признаков, в целом необходимо располагать системой средних величин, которые могут описать явление с разных сторон.
Существуют различные виды средних: средняя арифметическая; средняя геометрическая; средняя гармоническая; средняя квадратическая; средняя хронологическая.
Слайд 41
Средняя арифметическая
Средняя арифметическая простая (невзвешенная) равна сумме отдельных
значений признака, деленной на
число этих значений.
Отдельные значения признака
называют вариантами и обозначают через х (
совокупности обозначают через n, среднее значение признака - через
); число единиц
.Следовательно, средняя арифметическая
простая равна:
Пример 7. Имеются следующие данные о производстве рабочими продукции А за смену:
В данном примере варьирующий признак - выпуск продукции за смену.
Численные значения признака (16, 17 и т.д.) называют вариантами. Определим среднюю выработку продукции
рабочими данной группы:
Простая средняя арифметическая применяется в случаях, когда имеются отдельные значения признака, т.е.
данные не сгруппированы. Если данные представлены в виде рядов распределения или группировок, то
средняя исчисляется иначе.
Слайд 42
Пример 8. Имеются следующие данные о заработной плате
рабочих - сдельщиков:
По данным дискретного ряда распределения видно, что
одни и те же значения признака (варианты) повторяются
несколько раз. Так, варианта х встречается в совокупности 2 раза, а варианта х-16 раз и т.д.
Число одинаковых значений признака в рядах распределения называется частотой или весом и обозначается
символом n.
Вычислим среднюю заработную плату одного рабочего
в руб.:
Фонд заработной платы по каждой группе рабочих равен произведению варианты на частоту, а сумма этих
произведений дает общий фонд заработной платы всех рабочих.
В соответствии с этим, расчеты можно представить в общем виде:
Полученная формула называется средней арифметической взвешенной.
Слайд 43
Средняя гармоническая
Наряду со средней арифметической, в статистике применяется
средняя гармоническая величина, обратная средней арифметической из обратных значений
признака.
Cредняя гармоническая
простая
взвешенная
Слайд 44
Мода
Характеристиками вариационных рядов, наряду со средними, являются мода
и медиана.
Мода - это величина признака (варианта), наиболее часто
повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.
Пример 9. Распределение проданной обуви по размерам характеризуется следующими показателями:
В этом ряду распределения мода равна 41. Именно этот размер обуви пользовался наибольшим спросом покупателей.
Для интервальных рядов распределения с равными интервалами мода определяется по формуле:
- начальное значение интервала, содержащего моду;
- величина модального интервала;
- частота модального интервала;
- частота интервала, предшествующего модальному;
- частота интервала, следующего за модальным.
Слайд 45
Пример 10. Распределение предприятий по численности промышленно -
производственного персонала характеризуется следующими данными:
В этой задаче наибольшее число
предприятий (30) имеет численность работающих от 400 до 500 человек.
Следовательно, этот интервал является модальным интервалом ряда распределения.
Введем следующие обозначения:
= 400,
= 100,
= 30,
= 7,
= 19
Подставим эти значения в формулу моды и произведем вычисления:
Слайд 46
Медиана
Медиана - это варианта, расположенная в середине вариационного

ряда. Если ряд распределения дискретный и имеет нечетное число
членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд - это расположение единиц совокупности в возрастающем или убывающем порядке).
Например, стаж пяти рабочих составил 2, 4, 7, 8, 10 лет. В таком упорядоченном ряду медиана - 7 лет. По обе стороны от нее находится одинаковое число рабочих.
Если упорядоченный ряд состоит из четного числа членов, то медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда. Пусть теперь будет не пять человек в бригаде, а шесть, имеющих стаж работы 2, 4, 6, 7, 8 и 10 лет. В этом ряду имеются две варианты, стоящие в центре ряда. Это варианты 6 и 7. Средняя арифметическая из этих значений и будет медианой ряда:
Ме = (6 + 7) / 2 = 6,5 лет.
Пример 11. Определим медиану заработной платы рабочих.
Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается
до получения накопленной суммы частот, превышающей половину. В нашем примере сумма частот составила
ее половина - 20.
Накопленная сумма частот ряда получилась равной Варианта, соответствующая этой сумме, т.е. 160 руб., и есть
медиана ряда.
Если же сумма накопленных частот против одной из вариант равна точно половине сумме частот, то медиана
определяется как средняя арифметическая этой варианты и последующей.
Рассмотрим пример расчета медианы в дискретном ряду.
Слайд 47
Медиана интервального вариационного ряда распределения определяется по формуле
:
— начальное значение интервала, содержащего медиану;
— величина
медианного интервала;
— сумма частот ряда;
— сумма накопленных частот, предшествующих медианному интервалу;
— частота медианного интервала.
Пример 12 Определить медиану заработной платы.
Определим прежде всего медианный интервал. В данной задаче сумма накопленных частот, превышающая половину всех значений (41), соответствует интервалу 400 - 500. Это и есть медианный интервал, в котором находится медиана. Определим ее значение по приведенной выше формуле.
Известно, что:
Следовательно,
.
Слайд 48
Показатели вариации.
Различие индивидуальных значений признака внутри изучаемой совокупности

в статистике называется вариацией признака.
Термин "вариация" произошел от латинского
variatio –“изменение, колебание, различие”. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают случайную и систематическую вариацию признака.
Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов.
Абсолютные и средние показатели вариации
Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака
скрывается за средним.
Для характеристики колебаний признака используется ряд показателей. Наиболее простой из них - размах
вариации.
Размах вариации-разность между наибольшим ( ) и наименьшим ( ) значениями вариантов.
Пример 13.
Определяем показатель размаха вариации:
R = 130 - 90 = 40 млн. руб.
Этот показатель улавливает только крайние отклонения
и не отражает отклонений всех вариант в ряду.
Чтобы дать обобщающую характеристику
распределению отклонений, исчисляют среднее
линейное отклонение d, которое учитывает различие
всех единиц изучаемой совокупности.
Слайд 49
Среднее линейное отклонение (СЛО) определяется как средняя арифметическая
из отклонений индивидуальных значений от средней, без учета знака
этих отклонений:
Порядок расчета СЛО:
1) по значениям признака исчисляется средняя арифметическая:
2) определяются отклонения каждой варианты
от средней
3) рассчитывается сумма абсолютных величин отклонений:
4) сумма абсолютных величин отклонений делится на число значений:
Пример 14.
d=
=
Слайд 50
Если данные наблюдения представлены в виде дискретного ряда
распределения с частотами, среднее линейное отклонение исчисляется по формуле
средней арифметической взвешенной:
Порядок расчета СЛО взвешенного:
1) вычисляется средняя арифметическая взвешенная:
2) определяются абсолютные отклонения вариант от средней / /
3) полученные отклонения умножаются на частоты
4) находится сумма взвешенных отклонений без учета знака:
5) сумма взвешенных отклонений делится на сумму частот:
Слайд 51
Расчет дисперсии и среднеквадратического отклонения
Основными обобщающими показателями
вариации в статистике являются дисперсии и среднеквадратическое отклонение.
Дисперсия -
это средняя арифметическая квадратов отклонений каждого значения признака от общей средней, показывает меру разброса признака, обозначается
или D. В зависимости от исходных данных, дисперсия может вычисляться по средней арифметической простой или взвешенной:
— дисперсия невзвешенная (простая);
— дисперсия взвешенная.
Среднеквадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается S.
— среднеквадратическое отклонение невзвешенное;
—среднеквадратическое отклонение взвешенное.
Среднеквадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака
в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах,
гектарах и т.д.).
Слайд 52
Пример 15.
Исчислим среднюю арифметическую взвешенную:
шт
Значения отклонений от средней и их квадратов представлены в таблице. Определим дисперсию:
=1,48
Среднеквадратическое отклонение будет равно: шт
Слайд 53
Порядок расчета дисперсии простой:
1) определяют среднюю арифметическую
2)
возводят в квадрат среднюю арифметическую
3) возводят в квадрат каждую
варианту ряда
4) находим сумму квадратов вариант
5) делят сумму квадратов вариант на их число, т.е. определяют средний квадрат
6) определяют разность между средним квадратом признака и квадратом средней
Пример 16. Имеются следующие данные о производительности труда рабочих:
Произведем следующие расчеты:
шт.
Слайд 54
Расчет дисперсии в интервальном ряду распределения.
Порядок расчета дисперсии
взвешенной (по формуле
):
1)определяют среднюю арифметическую
2)возводят в квадрат полученную среднюю
3)возводят в квадрат каждую варианту ряда
4)умножают квадраты вариант на частоты
5)суммируют полученные произведения
6)делят полученную сумму на сумму весов и получают средний квадрат признака
7)определяют разность между средним значением квадратов и квадратом средней арифметической,
т.е. дисперсию
Пример 17. Определить дисперсию в дискретном ряду распределения
Слайд 55
Показатели относительного рассеивания.
Для характеристики меры колебания изучаемого признака

исчисляются показатели колебания в относительных величинах. Они позволяют сравнивать
характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
Коэффициент осцилляции отражает относительные колебания крайних значений признака вокруг средней.
(1)
Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от
средней величины.
(2)
Коэффициент вариации:
(3)
Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колебаний всех вариантов
совокупности, коэффициент вариации является наиболее распространенным показателем колебаний,
используемым для оценки типичности средних величин, при этом исходят из того, что если V больше 40 %, то
это говорит о значительных колебаниях признака в изучаемой совокупности.
Слайд 56
5.РЯДЫ ДИНАМИКИ
Основная цель статистического изучения динамики коммерческой деятельности

состоит в выявлении и измерении закономерностей их развития во
времени. Это достигается посредством построения и анализа статистических рядов динамики.
Рядами динамики называются статистические данные, отображающие развитие изучаемого явления во времени. В каждом ряду динамики имеются два основных элемента: показатель времени t; соответствующие им уровни развития изучаемого явления у. В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки).
Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим, ряды динамики подразделяются на моментные и интервальные.
Ряды динамики
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.
Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
Слайд 57
Ряды динамики могут быть полными и неполными.
Полный

ряд - ряд динамики, в котором одноименные моменты времени
или периоды времени строго следуют один за другим в календарном порядке или равноотстоят друг от друга.
Неполный ряд динамики - ряд, в котором уровни зафиксированы в неравноотстоящие моменты или периоды времени, например:
Приведение рядов динамики в сопоставимый вид.
Ряды динамики, изучающие изменение статистического показателя, могут охватывать значительный период времени, на протяжении которого могут происходить события, нарушающие сопоставимость отдельных уровней ряда динамики (изменение методологии учета, изменение цен и т.д.).
Для того, чтобы анализ ряда был объективен, необходимо учитывать события, приводящие к несопоставимости уровней ряда и использовать приемы обработки рядов для приведения их в сопоставимый вид.
Наиболее характерные случаи несопоставимости уровней ряда динамики:
-Территориальные изменения объекта исследования, к которому относится изучаемый показатель (изменение границ городского района, пересмотр административного деления области и т.д.).
-Разновеликие интервалы времени, к которым относится показатель. Так, например, в феврале - 28 дней, в марте - 31 день, анализируя изменения показателя по месяцам, необходимо учитывать разницу в количестве дней.
-Изменение даты учета. Например, численность поголовья скота в разные годы могла определяться по состоянию на 1 января или на 1 октября, что в данном случае приводит к несопоставимости.
-Изменение методологии учета или расчета показателя.
-Изменение цен.
-Изменение единиц измерения.
Слайд 58
Пример 18.
Динамика изменения численности населения района области по
состоянию на 1 января (в тыс. человек) представлена рядом
ди - в старых границах района.
В 1984 году произошло изменение административного деления области, и площадь района 1984 увеличилась, соответственно увеличилась и численность населения района:
- в новых границах района.
Для приведения ряда в сопоставимый вид необходимо для 1984 года знать численность населения в старых и новых границах района для определения коэффициента пересчета:
Все уровни ряда, предшествующие 1984 году, умножаются на коэффициент К и ряд принимает вид:
После этого преобразования ряда динамики возможен дальнейший анализ ряда (определение темпов роста и др.).
Слайд 59
Определение среднего уровня ряда динамики.
В качестве обобщенной характеристики
уровней ряда динамики служит средний уровень ряда динамики
В
зависимости от типа ряда динамики используются различные расчетные формулы.
Интервальный ряд абсолютных величин с равными периодами (интервалами времени):
Моментный ряд с равными интервалами между датами:
Моментный ряд с неравными интервалами между датами:
, где
- уровни ряда, сохраняющиеся без изменения на протяжении интервала времени
Слайд 60
Показатели изменения уровней ряда динамики
Одним из важнейших направлений

анализа рядов динамики является изучение особенностей развития явления за
отдельные периоды времени.
С этой целью для динамических рядов рассчитывают ряд показателей: К - темпы роста;
- абсолютные приросты;
- темпы прироста.
Темп роста - относительный показатель, получающийся в результате деления двух уровней одного ряда друг на друга. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем:
,либо как базисные, когда все уровни ряда сопоставляются с одним и
, выбранным за базу сравнения:
Темпы роста могут быть представлены в виде коэффициентов либо в виде процентов.
тем же уровнем
Абсолютный прирост - разность между двумя уровнями ряда динамики, имеет ту же размерность, что и уровни
самого ряда динамики. Абсолютные приросты могут быть цепными и базисными, в зависимости от способа
выбора базы для сравнения:
цепной абсолютный прирост -
базисный абсолютный прирост -
Для относительной оценки абсолютных приростов рассчитываются показатели темпов прироста.
Слайд 61
Темп прироста - относительный показатель, показывающий на сколько
процентов один уровень ряда динамики
больше (или меньше) другого,
принимаемого за базу для сравнения.
Базисные темпы прироста:
Цепные темпы прироста:
и
- абсолютный базисный или цепной прирост;
- уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов;
- уровень ряда динамики, выбранный за базу для определения i-го цепного абсолютного прироста.
К = К - 100 % (если темпы роста определены в процентах).
К = К - 1 или
Существует связь между темпами роста и прироста:
Если разделить абсолютный прирост (цепной) на темп прироста (цепной) за соответствующий период, получим показатель, называемый - абсолютное значение одного процента прироста:
Слайд 62
Пример 19. Выпуск продукции предприятия за 1985 —
1990 гг. характеризуются следующими данными
(в сопоставимых ценах), млн.
руб.:
Требуется произвести анализ динамики выпуска продукции предприятием за пять лет.
1. Определяем цепные и базисные темпы роста (К).
Цепные: Базисные:
2. Определяем цепной и базисный абсолютный прирост (
)
Цепные: Базисные:
3. Определяем цепные и базисные темпы прироста (
).
Цепные: Базисные:
Проверим связь между темпами роста и прироста.
Цепные темпы прироста:
и т.д.
Видим, что получаем такие же результаты.