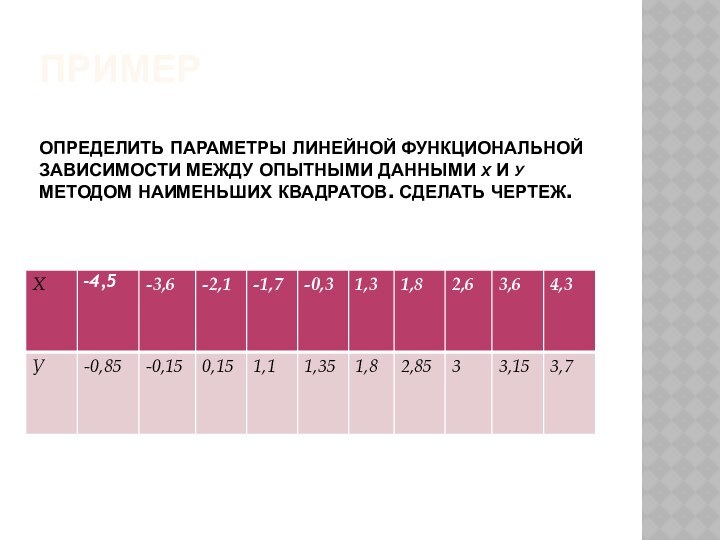
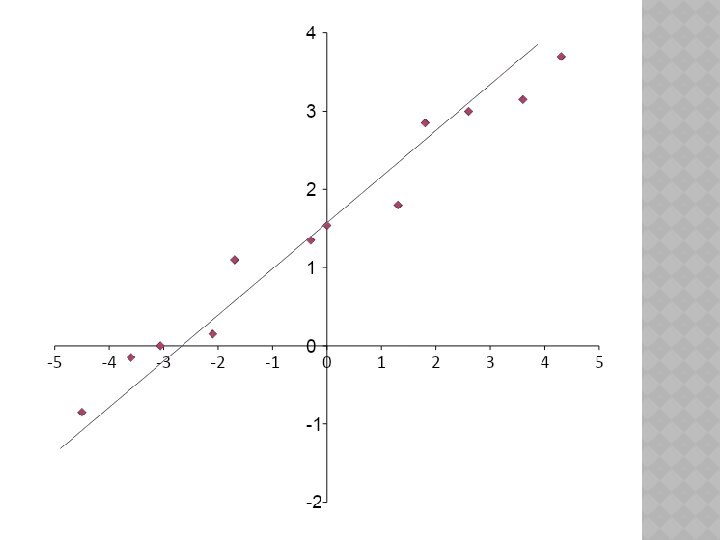
выражается в виде таблицы, полученной опытным путем. Это могут
быть результаты опыта или наблюдений, статической обработки материала и т.п.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть