- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Менелая
Содержание
- 2. МенелайМенелай Александрийский (ок. 100 н. э.) – древнегреческий математик и астроном.
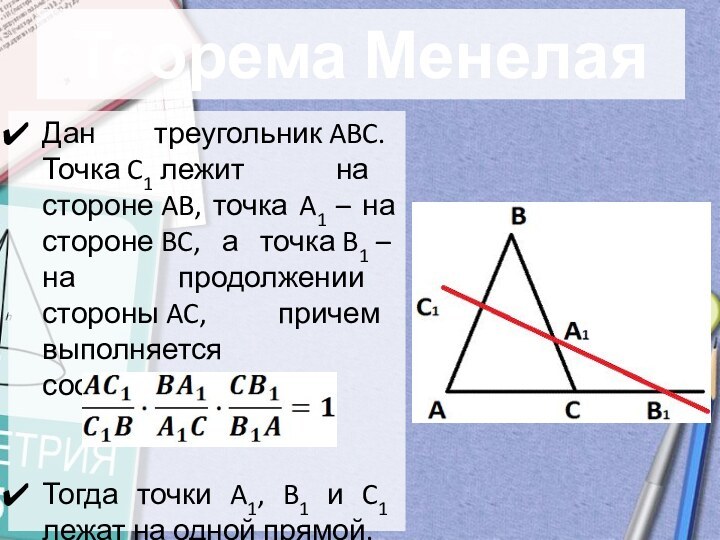
- 3. Теорема МенелаяДан треугольник ABC. Точка C1 лежит на стороне AB, точка
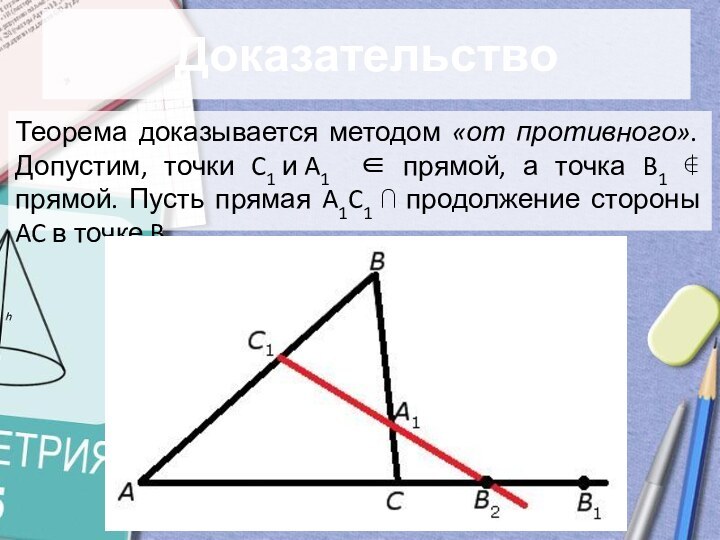
- 4. ДоказательствоТеорема доказывается методом «от противного». Допустим, точки
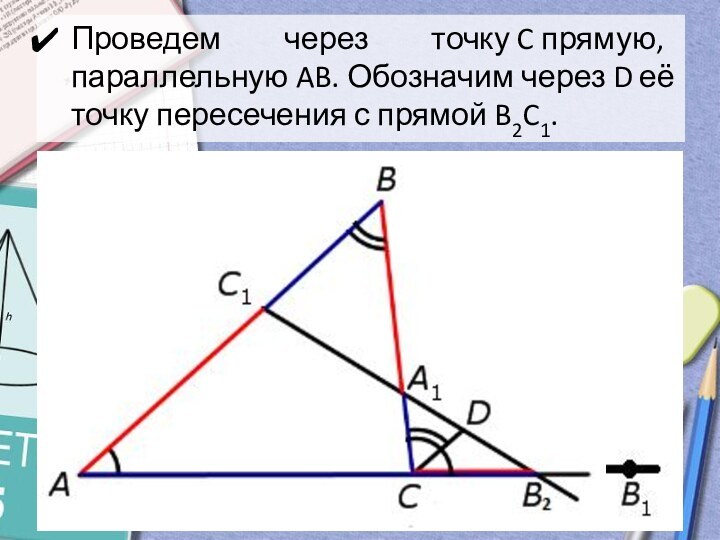
- 5. Проведем через точку C прямую, параллельную AB. Обозначим через D её точку пересечения с прямой B2C1.
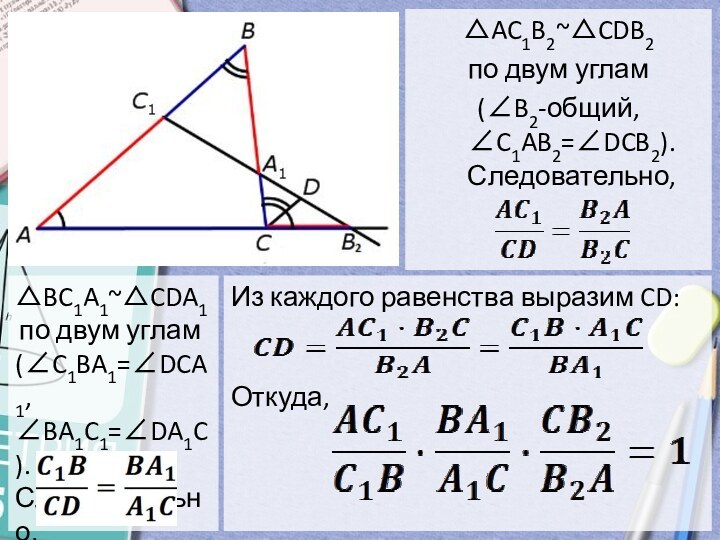
- 6. △AC1B2~△CDB2 по двум углам (∠B2-общий, ∠C1AB2=∠DCB2). Следовательно,△BC1A1~△CDA1 по двум углам (∠C1BA1=∠DCA1, ∠BA1C1=∠DA1C). Следовательно,Из каждого равенства выразим CD:Откуда,
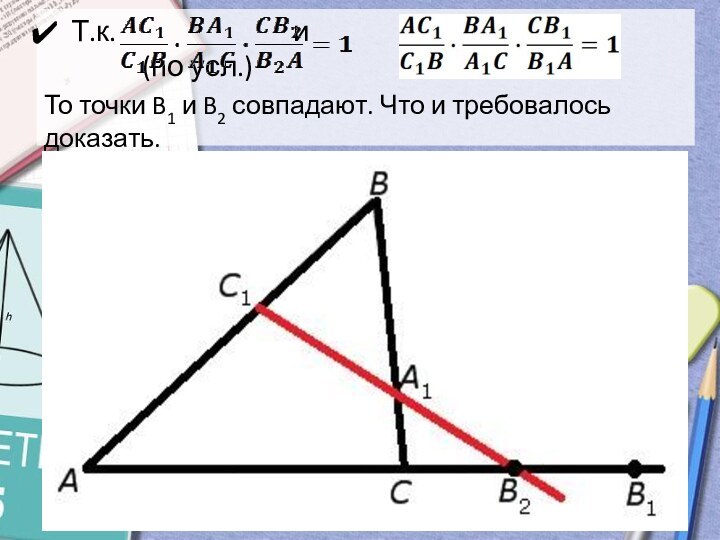
- 7. Т.к. и
- 8. Обратная теорема Прямая пересекает треугольник ABC, причем С1 –
- 9. ДоказательствоПроведем через точку C прямую, параллельную AB. Обозначим через D её точку пересечения с прямой B1C1.
- 10. △AC1B1~△CDB1 по двум углам (∠B1-общий, ∠C1AB1=∠DCB1). Следовательно,△BC1A1~△CDA1 по двум
- 11. Задача №1Сформулируйте теорему для данного рисунка.Прямая МВ пересекает две стороны и продолжение третьей стороны треугольника АDС.
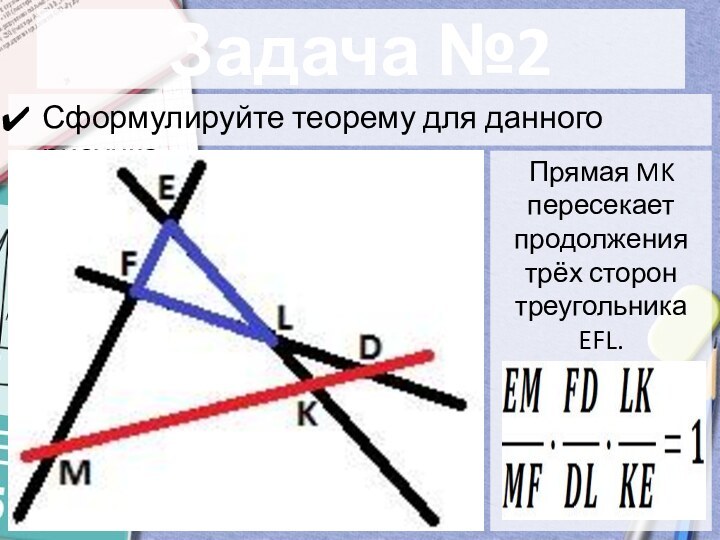
- 12. Задача №2Сформулируйте теорему для данного рисунка.Прямая MK пересекает продолжения трёх сторон треугольника EFL.
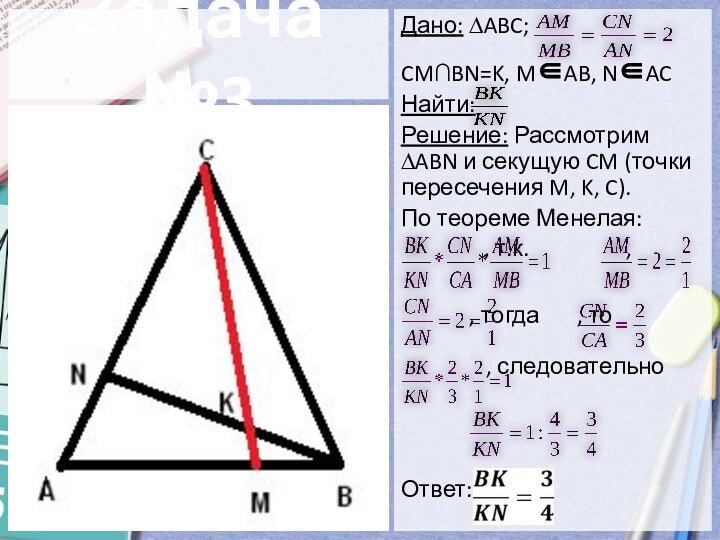
- 13. Задача №3Дано: ∆ABC; CM∩BN=K, MAB, NACНайти: Решение:
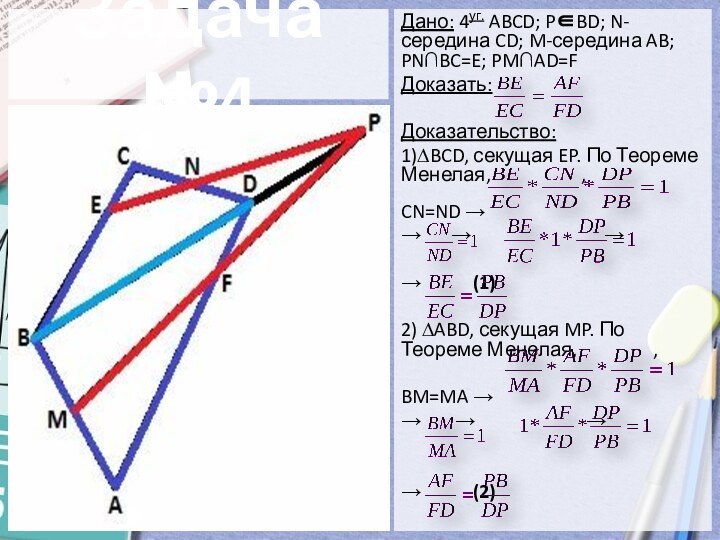
- 14. Задача №4Дано: 4уг. ABCD; PBD; N-середина CD;
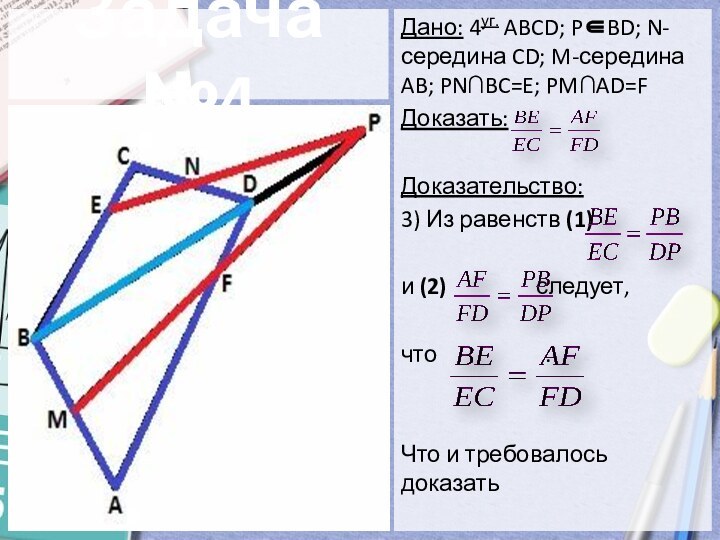
- 15. Задача №4Дано: 4уг. ABCD; PBD; N-середина CD;
- 16. Скачать презентацию
- 17. Похожие презентации
МенелайМенелай Александрийский (ок. 100 н. э.) – древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал 6 книг о вычислении хорд и 3 книги “Сферики’’, сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема



Слайд 2
Менелай
Менелай Александрийский (ок. 100 н. э.) – древнегреческий математик и астроном. Автор
Слайд 3
Теорема Менелая
Дан треугольник ABC. Точка C1 лежит на стороне AB, точка A1
– на стороне BC, а точка B1 – на продолжении стороны AC, причем
выполняется соотношениеТогда точки A1, B1 и C1 лежат на одной прямой.
Слайд 4
Доказательство
Теорема доказывается методом «от противного». Допустим, точки C1 и A1
∈ прямой, а точка B1 ∉ прямой. Пусть прямая
A1C1 ⋂ продолжение стороны AC в точке B2.Слайд 5 Проведем через точку C прямую, параллельную AB. Обозначим через D её точку пересечения
с прямой B2C1.
Слайд 6
△AC1B2~△CDB2
по двум углам
(∠B2-общий, ∠C1AB2=∠DCB2). Следовательно,
△BC1A1~△CDA1 по двум углам
(∠C1BA1=∠DCA1, ∠BA1C1=∠DA1C). Следовательно,
Из каждого равенства выразим CD:
Откуда,
Слайд 8
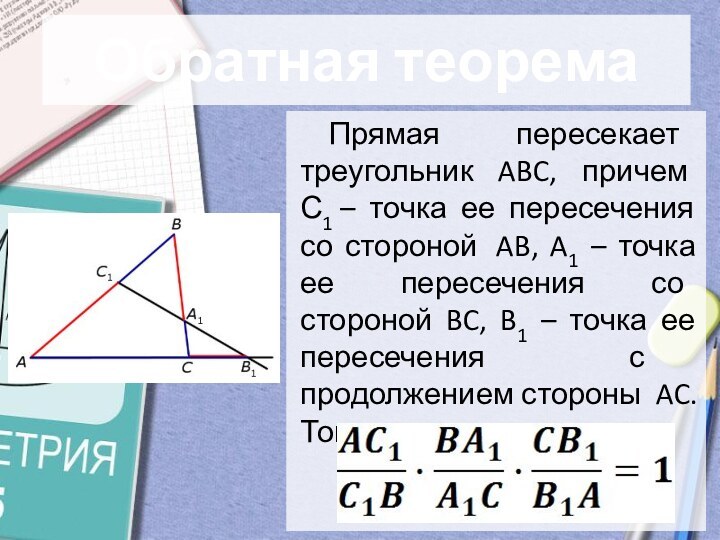
Обратная теорема
Прямая пересекает треугольник ABC, причем С1 – точка
ее пересечения со стороной AB, A1 – точка ее
пересечения со стороной BC, B1 – точка ее пересечения с продолжением стороны AC. Тогда верно равенство:
Слайд 9
Доказательство
Проведем через точку C прямую, параллельную AB. Обозначим через D её точку пересечения
с прямой B1C1.
Слайд 10
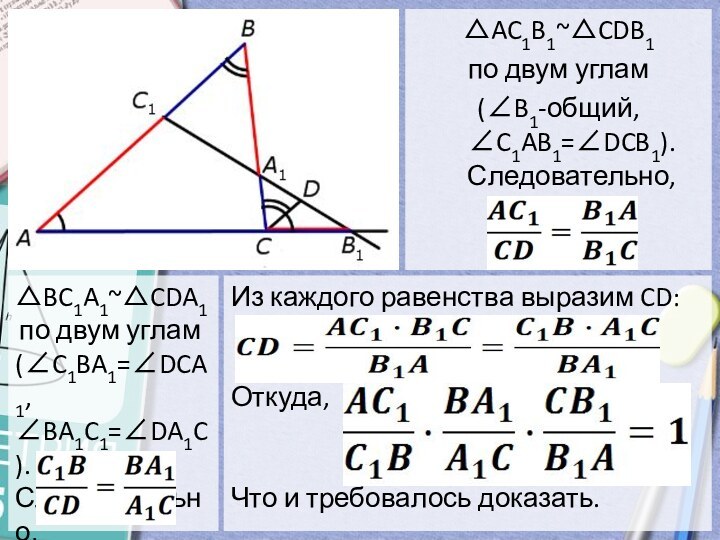
△AC1B1~△CDB1
по двум углам
(∠B1-общий, ∠C1AB1=∠DCB1). Следовательно,
△BC1A1~△CDA1 по двум углам
(∠C1BA1=∠DCA1, ∠BA1C1=∠DA1C). Следовательно,
Из каждого равенства выразим CD:
Откуда,
Что и требовалось доказать.
Слайд 11
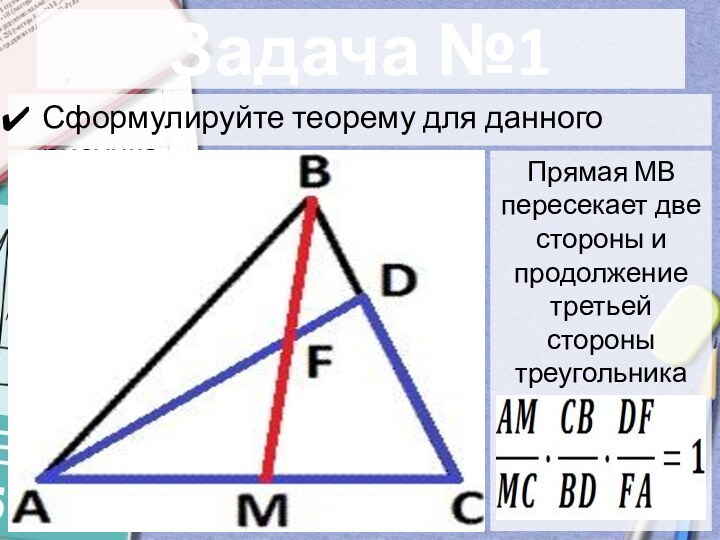
Задача №1
Сформулируйте теорему для данного рисунка.
Прямая МВ пересекает
две стороны и продолжение третьей стороны треугольника АDС.
Слайд 12
Задача №2
Сформулируйте теорему для данного рисунка.
Прямая MK пересекает
продолжения трёх сторон треугольника EFL.
Слайд 13
Задача №3
Дано: ∆ABC;
CM∩BN=K, MAB, NAC
Найти:
Решение: Рассмотрим
∆ABN и секущую CM (точки пересечения M, K, C).
По теореме Менелая:
, т.к. ,
, тогда , то
, следовательно
Ответ:
Слайд 14
Задача №4
Дано: 4уг. ABCD; PBD; N-середина CD; M-середина
AB; PN∩BC=E; PM∩AD=F
Доказать:
Доказательство:
1)∆BCD, секущая EP. По Теореме
Менелая, , CN=ND →
→ → →
→ (1)
2) ∆ABD, секущая MP. По Теореме Менелая, ,
BM=MA →
→ → →
→ (2)
Слайд 15
Задача №4
Дано: 4уг. ABCD; PBD; N-середина CD; M-середина
AB; PN∩BC=E; PM∩AD=F
Доказать:
Доказательство:
3) Из равенств (1)
и (2) следует,
что .
Что и требовалось доказать





























