Слайд 2
Пьер-Симо́н Лаплас (1749- 1827) - выдающийся французский математик, физик
и астроном; один из создателей теории вероятностей. Был членом
Французского Географического общества.
Абрахам де Муавр (1667- 1754) — английский математик французского происхождения. Член Лондонского королевского общества (1697), Парижской (1754) и Берлинской (1735) академий наук.
Слайд 3
Теорема Муавра - Лапласа - простейшая из предельных теорем теории
вероятностей.
В общем виде теорема доказана Лапласом в книге
«Аналитическая теория вероятностей» (1812). Один частный случай теоремы был известен Муавру (1730), в связи с чем она и называется теоремой Муавра-Лапласа.
Утверждает, что число успехов при многократном повторении одного и того же случайного эксперимента с двумя возможными исходами приблизительно имеет нормальное распределение.
Слайд 4
Рассмотрим последовательность из n независимых опытов, в каждом из которых
событие A может произойти с вероятностью p, либо не произойти - с вероятностью
q = 1 − p. Обозначим через Pn(m) вероятность того, что событие A произойдет ровно m раз из n возможных. Если n будет достаточно большим, то найти значение Pn(m) по теореме Бернулли становится нереально из-за огромного объема вычислений. Локальная теорема Муавра -Лапласа позволяет найти приближенное значение вероятности.
Слайд 5
Локальная теорема Муавра - Лапласа. Если в схеме Бернулли число
n велико, а число p отлично от 0 и 1, тогда:
Функция φ(x)
называется функцией Гаусса. Теорема Муавра-Лапласа утверждает, что асимптотическим выражением для биномиального распределения является нормальная функция.
Слайд 6
Для расчетов составлена таблица значений функции φ (x),
необходимо учитывать свойства:
1. φ(−x) = φ(x) - четная, в
таблице приведены значения функции лишь для положительных аргументов;
2. Функция φ(x) - монотонно убывающая. Предел φ(x) при x→∞ равен нулю.
3. Если х > 5, то можно считать, что φ(х) ≈ 0. Функция φ(х) уже при х = 5 очень мала: φ(5)=0,0000015. Поэтому таблица значений не продолжена для х > 5.
Слайд 7
Пример. Вероятность покупки при посещении клиентом магазина составляет
р = 0,75. Найти вероятность, что при 100 посещениях
клиент совершит покупку ровно 80 раз.
Решение. n = 100, m = 80, p = 0,75, q = 0,25.
Находим ,
определяем (1,16) = 0,2036, тогда:
Р100(80) =
Слайд 8
Задание. Вероятность выпуска бракованного изделия равна 0,02. Какова
вероятность того, что среди 2500 выпущенных изделий окажется 50
бракованных
Варианты ответов:
0,1045; 2) 0,86; 3) 0,0570;
4) 0,0172; 5) 0,3989.
Ответ: пункт 5
Слайд 10
Интегральная теорема Муавра – Лапласа. Если вероятность р
наступления события А в каждом испытании постоянна и отлична
от 0 и 1, то вероятность, что в n независимых испытаниях (n>>1) событие А состоится число раз, заключенное в границах от а до b включительно:
Слайд 11
где функция Ф (х) определяется равенством
Формула называется интегральной
формулой Муавра— Лапласа.
Получаемые по интегральной и локальной формулам
Муавра — Лапласа вероятности достаточно точны, если произведение nр составляет несколько сотен!!!
Слайд 12
Свойства функции Ф(х)
Функция Ф(х) нечетная, Ф (- х)
= - Ф(х).
Функция Ф(х) монотонно возрастающая.
Предел функции
Ф(х) при x→∞ равен 0,5.
Для всех значений х > 5 считают, что Ф (х) ≈ 0,5. Уже Ф (5) = 0,4999992, при увеличении х функция Ф (х) возрастает, но не может превосходить 0,5. Поэтому в таблицах функция дана для значений х < 5.
Слайд 13
Оценка отклонения относительной частоты от постоянной вероятности
Вероятность, что
в n независимых испытаниях, в каждом из которых вероятность
появления события А постоянна и равна р, абсолютная величина отклонения относительной частоты появления события А от его постоянной вероятности не превысит положительного числа , приближенно равна:
Слайд 14
Пример. Вероятность появления события в каждом из 625
независимых испытаний равна 0,8. Найти вероятность, что относительная частота
появления события отклонится от его вероятности по абсолютной величине не более, чем на 0,04.
Решение. По условию задачи: n = 625; p = 0,8; =0,04. Отсюда q =1– p = 0,2. Требуется найти вероятность:
Слайд 15
Для решения задачи воспользуемся формулой, определяющей оценку отклонения
относительной частоты от постоянной вероятности:
Ф(х) – интегральная функция Лапласа.
Найдем аргумент функции Лапласа:
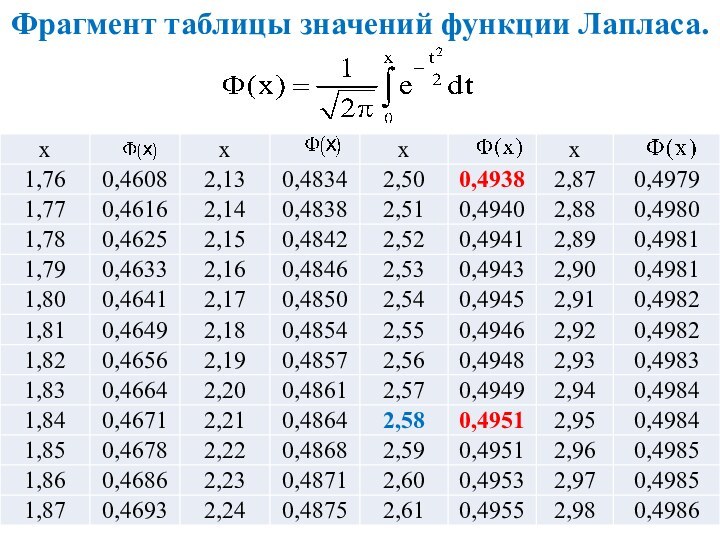
По табл. функции Лапласа: Ф(2,5) = 0,4938, т.е. 2Ф(х) = 0,9876.
Слайд 19
Пример. Страховая компания заключила 40000 договоров. Вероятность страхового
случая по каждому из них в течение года составляет
2%. Найти вероятность, что таких случаев будет не более 870.
Решение. По условию задачи n = 40000, p = 0,02. Находим np = 800, . Для вычисления Р (m 870) воспользуемся интегральной теоремой Муавра-Лапласа:
Р(0 < m 870) = Ф0(х2) –Ф0(х1), где
Слайд 20
Находим по таблице значений функции Лапласа:
Р(0
m 870) = Ф0(х2) – Ф0(х1) = Ф0(2,5)
– – Ф0(–28,57) = 0,4938 + 0,5 = 0,9938.
Ответ: P = 0,9938
Слайд 21
Пример. Вероятность появления события в каждом из 400
независимых испытаний равна 0,8. Найти такое положительное число ,
чтобы с вероятностью 0,99 абсолютная величина отклонения относительной частоты появления события от его вероятности не превышала .
Решение. По условию p = 0,8, n = 400. Используем следствие из интегральной т. Муавра-Лапласа:
. По
таблице для
функции Лапласа определяем
Отсюда, = 0,0516.
Слайд 23
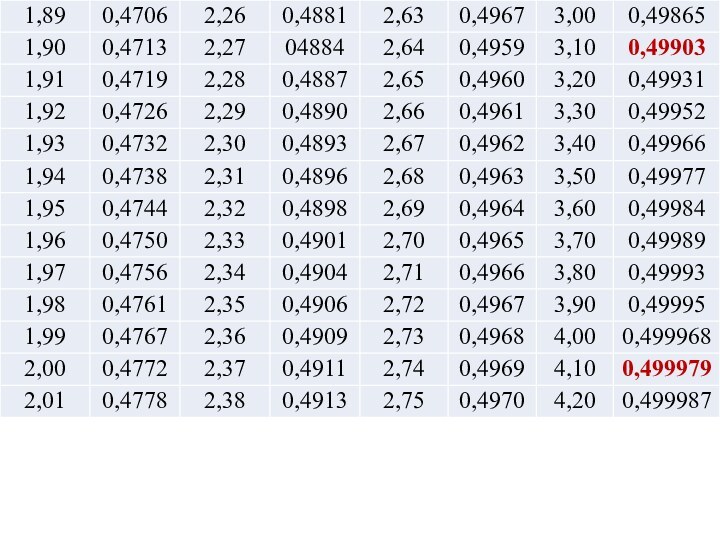
Фрагмент таблицы значений функции Лапласа.