- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ТЕОРЕМА ПІФАГОРА
Содержание
- 3. Для будь-яких трьох додатних чисел a, b
- 4. Доведення [ред.] Алгебраїчне доведення Квадрати утворюються з
- 5. Відстань між точками, що віддалені одна від
- 6. СоКрОвИщА ГЕОМЕТРІЇ
- 7. ДОВЕДЕННЯ ТЕОРЕМИ
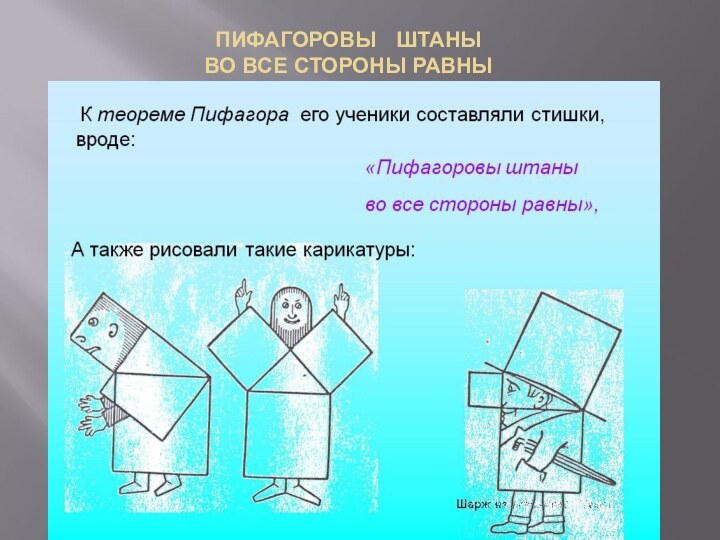
- 8. ПИФАГОРОВЫ ШТАНЫ ВО ВСЕ СТОРОНЫ РАВНЫ
- 11. Не знаєш теореми Піфагора, важай, що не
- 12. Скачать презентацию
- 13. Похожие презентации
Для будь-яких трьох додатних чисел a, b і c, для яких виконується рівняння a² + b² = c², існує прямокутний трикутник з катетами a та b і гіпотенузою c.



![ТЕОРЕМА ПІФАГОРА Доведення [ред.] Алгебраїчне доведення Квадрати утворюються з чотирьох прямокутних трикутників. Відомо понад](/img/tmb/14/1392097/9ecc6186f3d7cf8443c5d95c2c1b1c47-720x.jpg)