Презентация на тему Тренировочный вариант №3

х 67 х 87 х...х 1987 х 2007 ? 
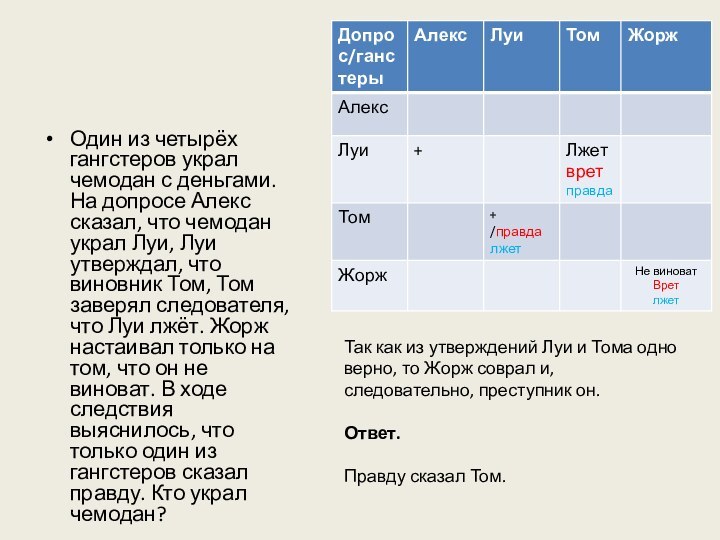
построим

таблицу произведений чисел, последняя цифра которых – 7

7*7=49
7*7*7=…3
7*7*7*7*=…1
7*7*7*7*7=…7
7*7*7*7*7*7=…9
7*7*7*7*7*7*7=…3
7*7*7*7*7*7*7*7=…1
7*7*7*7*7*7*7*7*7*=…7
7*7*7*7*7*7*7*7*7*7=…9
Заметить закономерность и использовать ее для решения задачи.
Осталось найти способ посчитать количество чисел, оканчивающихся 7 от 7 до 2007 (в каждом десятке одно только число оканчивается на 7)

201:4=50 (ост.1)
50 циклов (последние цифры произведений
9,3,1,7
Следовательно последняя цифра данного произведения - ………

на 4. Рома подсчитал сумму 1000 подряд идущих чисел

в Сашиной записи. Могло ли у него получиться в результате 20012002?

Из любых трёх чисел, идущих в Сашиной записи подряд, одно имеет остаток 1 пр делении на 4, другое – остаток 2, а оставшееся – остаток 3. Значит их сумма при делении на 4 даёт остаток 2. Среди первых 999 Роминых чисел есть ровно 333 таких тройки, сумма чисел в них даёт при делении на 4 такой же остаток, как 333 • 2, то есть 2. Оставшееся число на 4 не делится, поэтому вся сумма не может также давать остаток 2. А 20012002 даёт именно этот остаток.

столбы за окном: "один, два, ...". Боря не выговаривает

букву "Р", поэтому при счете он пропускает числа, в названии которых есть буква "Р", а называет сразу следующее число без буквы "Р". Миша не выговаривает букву "Ш", поэтому пропускает числа с буквой "Ш". У Бори последний столб получил номер "сто". Какой номер этот столб получил у Миши?

  Боря выговаривает числа, в записи которых нет цифр 3 и 4 – среди первых ста чисел таких  (10 – 2)2 = 64  (и для цифры десятков, и для цифры единиц есть по 8 вариантов), то есть на самом деле столбов было 64.    Миша же пропускает числа, в записи которых присутствует цифра 6. Поэтому, досчитав до 59, он пропустит 6 чисел – то есть ему останется посчитать еще  64 – (59 – 6) = 11  столбов. Отсчитывая эти 11 столбов, Миша пропустит все числа от 60 до 69, а также число 76. В результате последний столб получит у него номер  69 + 11 + 1 = 81.

На допросе Алекс сказал, что чемодан украл Луи, Луи

утверждал, что виновник Том, Том заверял следователя, что Луи лжёт. Жорж настаивал только на том, что он не виноват. В ходе следствия выяснилось, что только один из гангстеров сказал правду. Кто украл чемодан?

Так как из утверждений Луи и Тома одно верно, то Жорж соврал и, следовательно, преступник он.
Ответ.
Правду сказал Том.

из них перенести запятую на один знак влево, то

получим меньшее число. Чему равны эти числа?

При переносе запятой влево число увеличивается в 10 раз.
Если не переносить запятую, то числа равны.
а+10а=13,5927
а= 1,2357
Ответ: 1,2357 и 12,357

проведены 4 дуги равных окружностей, радиусом 4.
Криволинейный треугольник FCG,

составленный из ¼ дуги окружности, в верхнем правом углу равен криволинейному треугольнику EDF в левом верхнем углу. Т.о. нужно найти площадь фигуры «лепесток» BHEDFGB. Заметим так же, что чертеж содержит 2 равных треугольника ABC (ABCGHA) и ADC (ADCFEA), составленных из сторон квадрата и дуги окружности.
Площадь закрашенной фигуры BHEFCGB равна разности площади квадрата ABCD и двух равных криволинейных треугольников ABC и ADC, составленных из стороны квадрата и ¼ дуг и окружности.
4*4=16 – площадь квадрата
¼ (П*4*4)=4п – площадь ¼ круга
16-4п – площадь криволинейного треугольника
S=16-2(16-4п)=8п-16

А

В

С

D

E

F

G

H

могут разместиться 4 посетителей?
Обозначим буквами АВСД – посетителей
******* -

свободные кресла
1. АВСД******
2.А*ВСД*****
3.А**ВСД****
4.А***ВСД***
5.А****ВСД**
6.А*****ВСД
Заметим, что размещение ВСД возможно 6 способами(подумайте!)
ВСД, ВДС, СВД, СДВ, ……….

Т.О. применяя размещение ВСД (6 способами) получаем, что на каждый случай размещения 1, 2,3,4,5,6 добавляется 6 вариантов размещения ВСД – итого 6*6=36 вариантов.
Заметим, что 1 кресло может быть свободным:
*АВСД*****, и снова вариантов – 6 (какой последний?), добавим варианты размещения ВСД
И так перебираем все варианты с посетителем А на первом месте.

Продолжим размещение по типу 1,2,3,4,5,6, если на 1 месте сидит посетитель В - ВАСД******* , применяя размещение АСД (помним – 6 раз), итого размещение по первой В – тоже 36 вариантов.
Заметим, что вариантов с размещение посетителя В первым по порядку будет столько же…….
Продолжаем ….. Посетитель С
Посетитель Д
Всего - ********

на 1 процент, большее — на 4 процента. При

этом их сумма увеличилась на 3 процента. На сколько процентов увеличилась разница между числами?

Часть 1.
1,01а+1,04в=1,03(а+в)
Используем:
1,01а=(1+0,01)а
а+0,01а+в+0,04в=а+0,03+а+в+0,03в
Решим уравнение:
0,01в=0,02а,
очевидно в=2а,
а+в – 100%, т.е. 3*а – 100%.

Рассмотрим разность чисел (1,04 в - 1,01а), учитывая, что:
в больше а;
Используем преобразования, которые выполнили в 1 части;
в=2а, в-а=2а-а=а, т.о. (а - 100%)
1,04в – 1,01а=2,08а – 1,01а =1,07а
Составим пропорцию
1,07а - х%
а –в=а - 100%
Х=107
Ответ: 7%

делящиеся на 7, потом на 11, потом на 13.

Сколько чисел было вычеркнуто на третьем шаге? Сколько осталось не вычеркнутыми?

Вспомните, в 6 классе мы использовали «Решето Эратосфена» для нахождения простых чисел? Некоторые числа были зачеркнуты несколько раз. Используем «решето» в этой задаче.
Найдем количество чисел от1 до 1000 кратных 7
1000: 7= 142 (ост. 6), т.е. 142числа.
На 1 шаге было вычеркнуто 142 числа
Найдем количество чисел кратных 11
1000:11= 90(ост.10), т.е. 90чисел.
Но!! Обратим внимание на числа которые кратны одновременно и 7 и 11.
Найдем количество чисел кратных 7 и 11 –
1000: (7*11)=12 (ост.76), итого12.
Т.О. на 2 шаге вычеркнуты 90 чисел, которые кратны 11, но по 2 раза оказались вычеркнуты числа кратные 7 и 11 одновременно – таких чисел – 12, т.е.
всего на 2 шаге вычеркнуто – 142+90 -12=220 чисел.

Продолжим.
Количество чисел, кратных 13 –
Количество чисел кратных 13 и 11 –
Количество чисел кратных 13 и 7
Количество чисел кратных 7,11 и 13 –
На третьем шаге вычеркнуто
142+90+76 –(12 +6+10+0) =

выше любого семиклассника. Петя сказал: любой семиклассник ниже хотя

бы одного из восьмиклассников. Сказали они одно и то же (хотя разными словами) или разное?

ВАСЯ: один из восьмиклассников выше любого семиклассника
все семиклассники ниже одного (только одного) из восьмиклассника.

ПЕТЯ: любой семиклассник ниже хотя бы одного из восьмиклассников
Хотя бы один – не менее одного
Всегда найдется (один, два, три….) восьмиклассник, который ниже семиклассника.

Ответ: разное

5, …, 16 (каждое по одному разу) в таком

порядке, чтобы сумма любых четырёх подряд идущих чисел делилась бы на 3?

Сумма чисел делится на 3 в том случае, если сумма остатков от деления каждого числа на 3 также кратна 3.
1 – отс.2
2- ост.1
3 -ост.0
4- ост.1
5- отс.2
6 –ост.0
И.д……продолжите самостоятельно до 16.

Собираем группы чисел по 4, таким образом, чтобы сумма остатков была кратна 3.
1+2+3+6 (ост. 2+1+0+0)
4+5+7+8 (ост.1+2+1+2)
9+10+11+13(ост.0+1+1+1)
12+14+15+16(ост.2+0+1)
Есть другие варианты????

ли противоположные углы коробки будут максимально удалёнными друг от

друга точками на коробке, если считать расстояние по поверхности (сколько ползти мухе), или не всегда

Попробуйте двигаться между противоположными углами коробки не вдоль ребер, а по грани коробки или по диагонали грани.
Начертите все возможные пути, измерьте.
Ответ на вопрос – всегда или не всегда?

1×2 квадрат 5×5? (Если можно, покажите, как; если нет,

докажите, что невозможно.)

Площадь доминошки – 2
Площадь квадрата – 25
Вспомните принцип четности
Ответ: нельзя

Тот же вопрос для квадрата 5×5 с вырезанной центральной клеткой
Площадь квадрата-24.
Площадь целых горизонтальных полос -8 ед.
Площадь оставшихся часте1 –по 2 ед.
Ответ: можно