- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ВВЕДЕНИЕ В ЛОГИКУ
Содержание
- 2. . М.В. Ломоносов
- 3. ВведениеНемного историиТеория множествПостроение таблицы истинностиАлгебра высказыванийСодержание
- 4. В процессе своей жизнедеятельности человек познает мир
- 5. Логика и интуиция – два противоположных и
- 6. Таким образом. Интуиция является антиподом, противовесом логики
- 7. Термин «логика» – наука о способах доказательств
- 8. Считается, что первые работыпо логике появились в
- 9. 2-й этап появление математическойили символической логикисвязан с
- 10. Первая реализация идей Лейбница принадлежит английскому ученому
- 11. Логика была значительно развита в работахшотландского логика
- 12. Немалый вклад в развитие логики внесли и
- 13. Под множеством понимают объединение в одно целое
- 14. Объекты, образующие множество, называются элементами множества (обозначаются
- 15. Множество, содержащее конечное число элементов, называется конечным
- 16. Если множество конечно, то
- 17. Часто приходится определять принадлежность данного элемента конкретному
- 18. Пример 5.Мы говорим, что число 5 натуральное,
- 19. Пример 6.Число 5,2 не принадлежит множеству натуральных
- 20. Множества и равны
- 21. Если
- 22. Если в рамках некоторого класса задач рассматриваются
- 23. Множество может быть задано:перечислением всех его элементов.
- 24. В ряде случаев одно и то
- 25. Отношения между множествами. Наглядно отношения между множествами изображают
- 26. Объединение множеств
- 27. Пересечение множеств
- 28. Разность множеств
- 29. Симметричная разность (А ÷ В) — это
- 30. Дополнением множества А до множества U (обозначается
- 31. Придумайте и запишите элементы множества, используя рисунок.теория множеств
- 32. Основные свойства операций над множествами.Для всех множеств
- 33. теория множеств
- 34. Таблицу, показывающую, какие значения принимает сложное высказывание
- 35. Порядок действий: Количество строк в таблице Q=2n,
- 36. разделить колонку значений первой переменной пополам и
- 37. 4. Провести заполнение таблицы истинности по столбикам, выполняя логические операции.111100000010001000101111
- 38. алгебра высказываний
- 39. алгебра высказываний
- 40. алгебра высказываний
- 41. алгебра высказываний
- 42. Скачать презентацию
- 43. Похожие презентации









































Слайд 3
Введение
Немного истории
Теория множеств
Построение таблицы истинности
Алгебра высказываний
Содержание
Слайд 4 В процессе своей жизнедеятельности человек познает мир (получает
информацию). Процессу познания сопутствует мышление. Мышление управляет действиями человека,
следит за тем, чтобы соблюдался определенный порядок, последовательность его действий.Мыслительная деятельность человека представляет собой сложный и многогранный процесс, происходящий как на сознательном. Так и на бессознательном уровнях. Это высшая ступень человеческого познания. Способность к адекватному отражению предметов и явлений действительности, т.е. к нахождению истины.
Введение
Слайд 5 Логика и интуиция – два противоположных и неразрывно
связанных между собой свойства человеческого мышления.
Логическое (дедуктивное) мышление отличается
тем, что оно от истинных посылок всегда приводит к истинному заключению, не опираясь при этом на опыт, интуицию и другие внешние факторы.Интуиция ( от лат. intuitio – «пристальное всматривание») представляет собой способность постижения истины путем прямого её усмотрения без основания с помощью логического строгого доказательства.
Введение
Слайд 6
Таким образом.
Интуиция является антиподом,
противовесом логики и
строгости.
Логическая часть мыслительного процесса протекает на уровне сознания,
интуитивная
– на подсознательном уровнеВведение
Слайд 7 Термин «логика» – наука о способах доказательств и
опровержений – происходит
от греч.
(логос), что означает «слово», «понятие», «смысл»Введение
Слайд 8
Считается, что первые работы
по логике появились в V
в. до н. э.
Основоположником логики как
науки является древнегреческий
философ и ученый
Аристотель (384-322 гг. до н.э.)
Он в своем труде «Аналитики»
систематизировал известные до него сведения, и эта система стала называться
формальная логика.
Он впервые разработал теорию дедукции, т.е.
теорию логического вывода
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ
Слайд 9
2-й этап появление математической
или символической логики
связан с применением
в логике
математических методов, начало,
которому положил немецкий ученый и философ
Готфрид Вильгельм Лейбниц (1646-1716 гг.)
Он пытался построить универсальный язык, с помощью которого можно было решать споры между людьми, а затем и вовсе все «идеи заменить вычислениями» .
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ
Слайд 10
Первая реализация идей Лейбница
принадлежит английскому ученому Дж.Булю.
Джордж Буль (1815-1864 (1815-1864 гг)
основоположник математической логики,
как самостоятельной
дисциплины. В его работах логика обрела свой алфавит, свою орфографию и грамматику. Поэтому начальный раздел математической логики называют алгеброй логики, или булевой алгеброй.
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ
Слайд 11
Логика была значительно развита в работах
шотландского логика А.
де Моргана (1806-1871 гг.)
английского логика У.Джевонса (1835-1882 гг.)
американског логика
Ч. Пирса (1839-1914 гг.)немецкого алгебраиста и логика Э. Шрёдера (1841-1902 гг.)
русского математика, астронома и логика
П.С. Порецкого (1846-1907 гг.)
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ
Слайд 12 Немалый вклад в развитие логики внесли и советские
математики Н.А. Васильев, И.И. Жегалкин, А.Н. Колмогоров, П.С. Новиков,
А.А. Марков, А.И. Мальцев, С.А. Яновская.XX век – это период начала глубокого проникновения идей и методов математической логики в технику, прежде всего в процесс конструирования и создания ЭВМ, в программирование, кибернетику, вычислительную математику, структурную лингвистику.
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ
Слайд 13 Под множеством понимают объединение в одно целое объектов,
хорошо различимых человеческой интуицией или мыслью.
Множество – это совокупность
объектов любой природы, рассматриваемая как единое целое.Множества обозначают прописными латинскими буквами A, B, M, …
Пример. N = {1, 2, 3, …} – множество целых чисел
теория множеств
Слайд 14 Объекты, образующие множество, называются элементами множества (обозначаются строчными
буквами).
Если элемент входит в множество
, то это обозначается так : .Запись означает, что элемент не принадлежит множеству .
теория множеств
Слайд 15 Множество, содержащее конечное число элементов, называется конечным (в
противном случае — бесконечным).
Пример 1.
Множество гласных букв в
слове “математика” состоит из трёх элементов – это буквы “а”, “е”, “и”, причем, гласная считается только один раз, т.е. элементы множества при перечислении не повторяются.Пример 2.
Множество натуральных чисел бесконечно.
теория множеств
Слайд 16 Если множество конечно, то число
его элементов называется мощностью множества и обозначается
.Если множество не содержит ни одного элемента, то оно называется пустым множеством и обозначается символом .
Пример 3.
Множество действительных корней уравнения x2 +1=0.
Пример 4.
Множество людей, проживающих на Солнце.
теория множеств
Слайд 17
Часто приходится определять принадлежность данного элемента конкретному множеству.
Множество
является подмножеством множества ,
если любой элемент принадлежит также множеству Это свойство обозначается(читается: включает или равно ).
теория множеств
Слайд 18
Пример 5.
Мы говорим, что число 5 натуральное, т.е.
утверждаем, что число 5 принадлежит множеству натуральных чисел. Символически
принадлежность множеству записывается с помощью знака . В данном случае символическая запись будет такой: 5 N. Читается: “5 принадлежит множеству натуральных чисел”.теория множеств
Слайд 19
Пример 6.
Число 5,2 не принадлежит множеству натуральных чисел,
т.к. не является натуральным числом. Символически отношение “не принадлежит”
записывается с помощью знака (реже ). Таким образом, здесь имеем: 5,2 NЧитается: “5,2 не принадлежит множеству натуральных чисел”.
теория множеств
Слайд 20 Множества и равны тогда
и только тогда, когда их элементы совпадают. В этом
случае пишут .Так как при равенстве множеств и во множестве нет элементов, не принадлежащих , а в нет элементов, не принадлежащих , то признаком равенства множеств является одновременное выполнение двух условий: и .
теория множеств
Слайд 21 Если
и , то
множество называется собственным подмножеством множества Обозначается (строгое включение).Одним из частных случаев является ситуация, когда элементами некоторого множества являются другие множества.
Например, пусть — множество футболистов команды «Спартак», — множество команд высшей лиги. Тогда .
теория множеств
Слайд 22 Если в рамках некоторого класса задач рассматриваются различные
множества, то полная совокупность всех элементов, из которых могут
формироваться все множества и подмножества, образует универсальное множество — «универсум» или полное пространство.Обозначается универсальное множество символом (генеральная совокупность).
теория множеств
Слайд 23
Множество может быть задано:
перечислением всех его элементов. Например,
, ;
порождающей процедурой. Порождающая процедура представляет собой правило получения элементов множества на основе уже имеющихся элементов либо из других объектов. Элементами множества считаются все объекты, которые получены с помощью этой процедуры;
описанием характеристик и свойств, которыми обладают все элементы множества.
Например, . .
теория множеств
Слайд 24 В ряде случаев одно и то же
множество может быть задано разными способами.
Пример: Множество натуральных чисел,
меньших, чем 10.1. N<10={1; 2; 3; 4; 5; 6; 7; 8; 9}.
2. N<10={z│z<10, z Є N}.
Одно и то же множество может быть задано с помощью различных характеристических свойств.
Пример: Множество квадратов.
1. A={x│x – ромб с прямыми углами}.
2. A={ x│x – прямоугольник с равными сторонами}.
. .
теория множеств
Слайд 25
Отношения между множествами.
Наглядно отношения между множествами изображают при
помощи особых чертежей, называемых КРУГАМИ ЭЙЛЕРА (или диаграммами Эйлера
– Венна).Для этого множества, сколько бы они ни содержали элементов, представляют в виде кругов или любых других замкнутых кривых (фигур)
теория множеств
U
A
B
C
Слайд 26 Объединение множеств
— это множество, состоящее из тех элементов,
которые принадлежат хотя бы одному из исходных множеств:или Пример: Если
Операции над множествами удобно представлять с помощью диаграммы Эйлера - Венна — замкнутой линии, ограничивающей элементы одного множества.
теория множеств
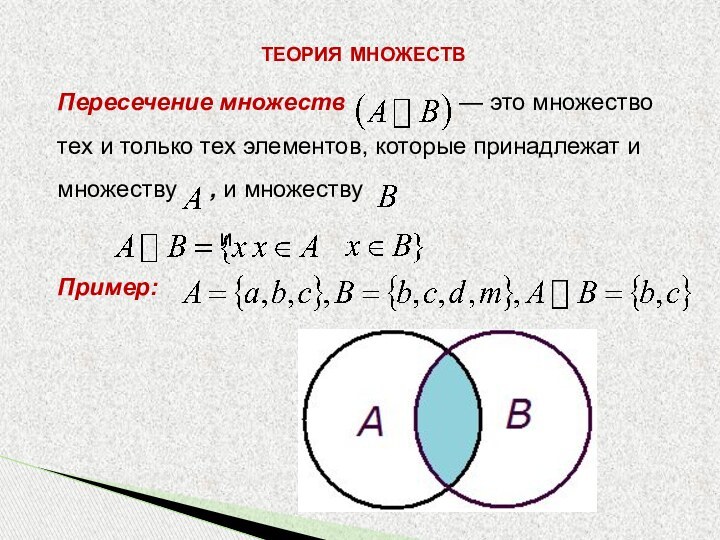
Слайд 27 Пересечение множеств
— это множество тех и только тех
элементов, которые принадлежат и множеству , и множествуи
Пример:
теория множеств
Слайд 28 Разность множеств
— это множество, состоящее из тех и
только тех элементов множества , которые не содержатся в множестве .и
Если , то
теория множеств
Слайд 29 Симметричная разность (А ÷ В) — это множество
элементов, принадлежащих множествам А или В за исключением их
общих элементови или и
теория множеств
Слайд 30 Дополнением множества А до множества U (обозначается
) называется множество всех элементов U, не
принадлежащих множеству А.теория множеств
Слайд 32
Основные свойства операций над множествами.
Для всех множеств А,
В, С и универсального множества U справедливы следующие равенства:
теория
множеств
Слайд 34
Таблицу, показывающую, какие значения принимает сложное высказывание при
всех сочетаниях значений входящих в него простых высказываний (переменных),
называют таблицей истинности сложного высказывания ( логической формулы).По формуле логической функции легко рассчитать ее таблицу истинности, соблюдая приоритет логических операций и действия в скобках.
Построение таблицы истинности
по логическому выражению
Слайд 35
Порядок действий:
Количество строк в таблице Q=2n, где
n - количество переменных (аргументов), здесь n = 3
(А, В, С) и тогда Q=23=82. Количество столбцов = число переменных + число операций (здесь 3+3=6 столбцов)
3. Выписать наборы входных переменных. Это удобнее сделать так:
Пример. Построим таблицу истинности следующей функции:
Построение таблицы истинности
по логическому выражению
Слайд 36 разделить колонку значений первой переменной пополам и заполнить
верхнюю половину 0, нижнюю половину 1.
разделить колонку значений второй
переменной на 4 части и заполнить каждую четверть чередующимися группами 0 и 1 , начиная опять с группы 0.продолжить деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами из 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа. (Можно заполнять все колонки, начиная с группы единиц.)
Построение таблицы истинности
по логическому выражению