Слайд 2
В вычислительной технике используются системы двух классов:
-Комбинационные
системы
Особенности: имеют функциональную зависимость между входными и выходными
сигналами y(t)=f(x(t), не имеют элементов памяти.
Цифровые автоматы (схемы второго класса или просто автоматы)
Особенности: содержат в своем составе запоминающие элементы, выходные сигналы зависят не только от входных(в один и тот же момент времени), но и от состояния схемы, которое зависит от поступивших в предыдущие моменты времени входных сигналов.
Автомат-это дискретный преобразователь информации, способный принимать различные состояния, переходить под воздействием входных сигналов из одного состояния в другое и выдавать различные выходные сигналы
Слайд 3
Математической моделью конечного автомата является абстрактный автомат, с
одним входным и выходным каналом:
X(x1, …, xF)--->A(a0, ..., aM)--->Y(y1,
…, yG)
Автомат функционирует в дискретные моменты времени, интервал между которыми Т (такт). В каждый дискретный момент времени на вход автомата поступает одна буква входного алфавита, автомат переходит из одного состояния в другое и выдается одна буква выходного алфавита. В зависимости от такта Т, различают автоматы синхронного действия (T = const) и асинхронного действия (T≠const).
Слайд 4
Детерминированные автоматы
Для задания конечного автомата S необходима
совокупность из пяти объектов: S{A, X, Y, d, l}
A = {a0, a1, a2, ..., am, ..., aM} – множество состояний автомата,
X = {x1, x2, …, xf ,…, xF} – множество входных сигналов или входной алфавит,
Y = {y1, y2, …, yg,…, yG} – множество выходных сигналов или выходной алфавит,
d – функция переходов, определяющая состояние автомата в момент времени (t + 1) в зависимости от состояния автомата и входного сигнала в момент времени t, т.е. a(t + 1) = d [a(t), x(t)],
l – функция выходов, определяющая значение выходного сигнала в зависимости от состояния автомата и входного сигнала в тот же момент времени, т.е. y(t) = l[a(t), x(t)].
Для того, чтобы автомат был конечным необходимо чтобы множества A, X, Y были конечны
Слайд 5
Принцип работы детерминированного автомата:
В каждый момент времени t
он находится в определенном состоянии a(t) из множества А
возможных состояний, причем в начальный момент времени t = 0 он находится в состоянии a0. Автомат воспринимает входной сигнал x(t), выдает выходной сигнал:
y(t) = l[a(t), x(t)]
и переходит в состояние:
a(t + 1) = d[a(t), x(t)]
Таким образом:
Детерминированными называют автоматы, которые каждой паре символов a(t) и x(t) ставит в однозначное соответствие пару символов a(t + 1) и y(t)
Слайд 6
Преобразование информации в детерминированных автоматах
1. Любое входное слово
длиною l букв преобразуется в выходное слово той же
длины.
2. Если каждый раз перед подачей входных сигналов автомат находится в одном и том же состоянии, то при совпадении в двух входных словах первых l1 букв, в выходных словах первые l1 букв также совпадут.
Кроме детерминированных автоматов существуют вероятностные автоматы, в которых переход из одного состояния в другое под воздействием случайных или детерминированных входных сигналов происходит случайно. Работа таких автоматов описывается уже матрицей переходов d, элементами которой являются вероятности переходов из одного состояния в другое.
Слайд 7
Автоматы Мили и Мура
Применяемые на практике автоматы принято
разделять на два класса – это автоматы Мили и автоматы Мура,
названные так по имени американских ученых, которые впервые начали их изучать
Автомат Мили— конечный автомат, выходные сигналы которого зависят как от состояния автомата, так и от значения входного сигнала
Закон функционирования автомата Мили
a(t + 1) = d [a(t), x(t)],
y(t) = l[a(t), x(t)]
Слайд 8
Автомат Мура- конечный автомат, входные сигналы которого y(t)
в каждый дискретный момент времени t однозначно определяется состоянием
автомата в тот же момент времени и не зависят от входного сигнала
a(t + 1) = d [a(t), x(t)],
y(t) = l[a(t)].
Слайд 9
Способы задания автоматов
Чтобы задать конечный автомат S, необходимо
описать все элементы множества S = {A, X, Y,
d, l},
Т.е. необходимо описать входной и выходной алфавиты и алфавит состояний, а также функции переходов d и выходов l. При этом среди множества A = {a0, a1, ... aM} необходимо выделить начальное состояния a0, в котором автомат находится в момент времени t = 0. Существует несколько способов задания работы автомата, но наиболее часто используются табличный и графический.
Слайд 10
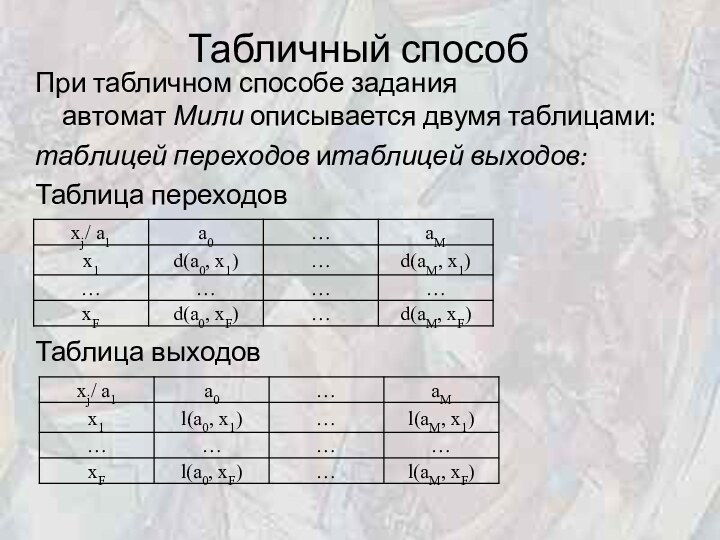
Табличный способ
При табличном способе задания автомат Мили описывается двумя таблицами:
таблицей
переходов итаблицей выходов:
Таблица переходов
Таблица выходов
Слайд 11
Строки этих таблиц соответствуют входным сигналам x(t), а
столбцы – состояниям. На пересечении столбца ai и строки xj в
таблице переходов ставится состояние as = d[ ai, xj], в которое автомат перейдет из состояния ai под воздействием сигнала xj, а в таблице выходов – соответствующий этому переходу выходной сигнал yg = l[ai, xj]. Иногда автомат Мили задают совмещенной таблицей переходов и выходов: xj/ a1
Слайд 12
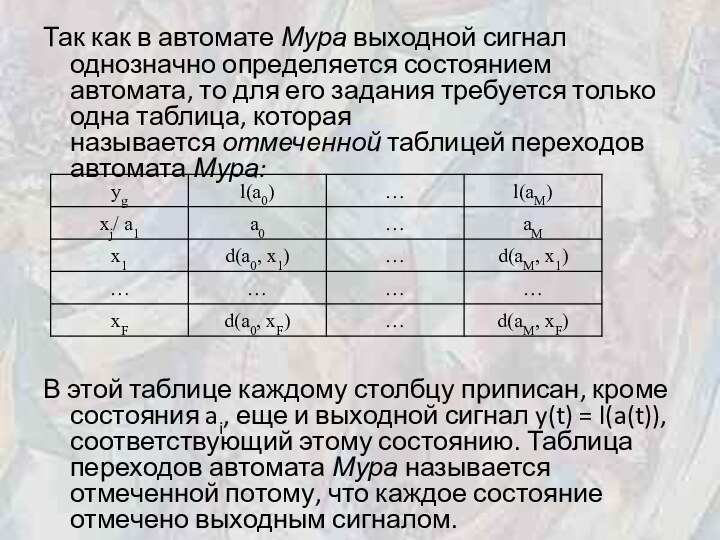
Так как в автомате Мура выходной сигнал однозначно определяется состоянием
автомата, то для его задания требуется только одна таблица,
которая называется отмеченной таблицей переходов автомата Мура:
В этой таблице каждому столбцу приписан, кроме состояния ai, еще и выходной сигнал y(t) = l(a(t)), соответствующий этому состоянию. Таблица переходов автомата Мура называется отмеченной потому, что каждое состояние отмечено выходным сигналом.
Слайд 13
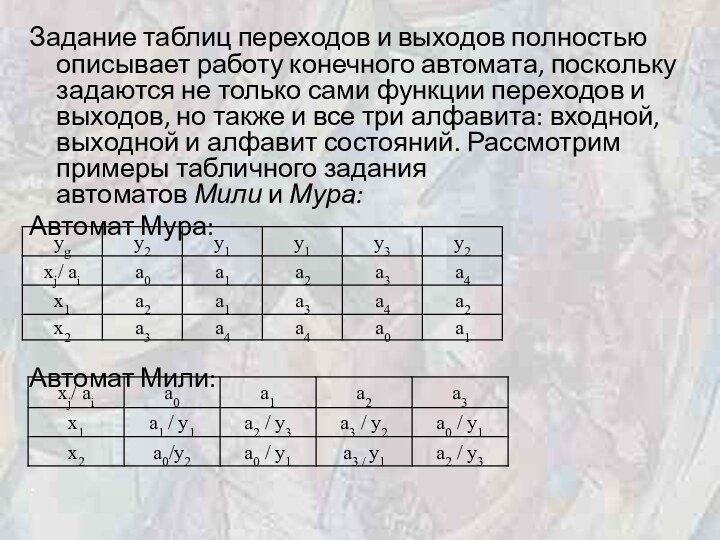
Задание таблиц переходов и выходов полностью описывает работу
конечного автомата, поскольку задаются не только сами функции переходов
и выходов, но также и все три алфавита: входной, выходной и алфавит состояний. Рассмотрим примеры табличного задания автоматов Мили и Мура:
Автомат Мура:
Автомат Мили:
.
Слайд 14
По этим таблицам можно найти реакцию автомата на
любое входное слово.
Для автомата Мура:
x1 x2 x2 x2 x1
a0 a2 a4 a1a4
y2 y1 y2 y1y2
Для автомата Мили:
x1 x2 x2 x2 x1
a0 a1 a0 a0 a0 a1
y1 y1 y2 y2 y1
Слайд 15
Графический способ
Этот способ основан на использовании ориентированных связных
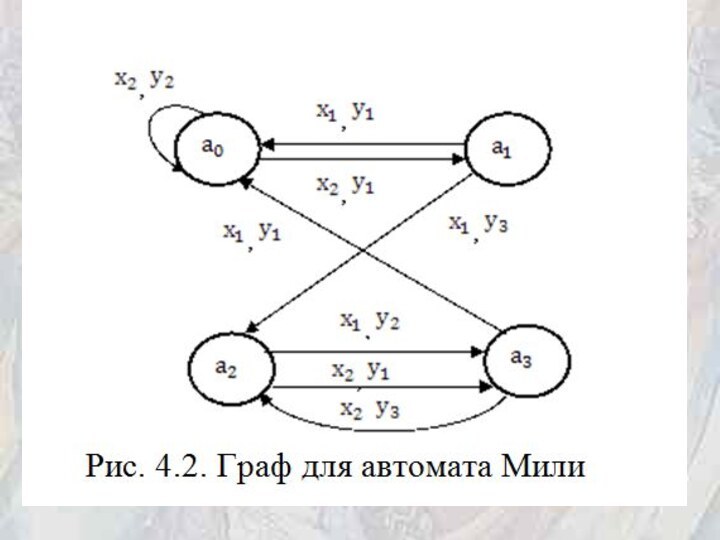
графов. Вершины графов соответствуют состояниям автомата, а дуги –
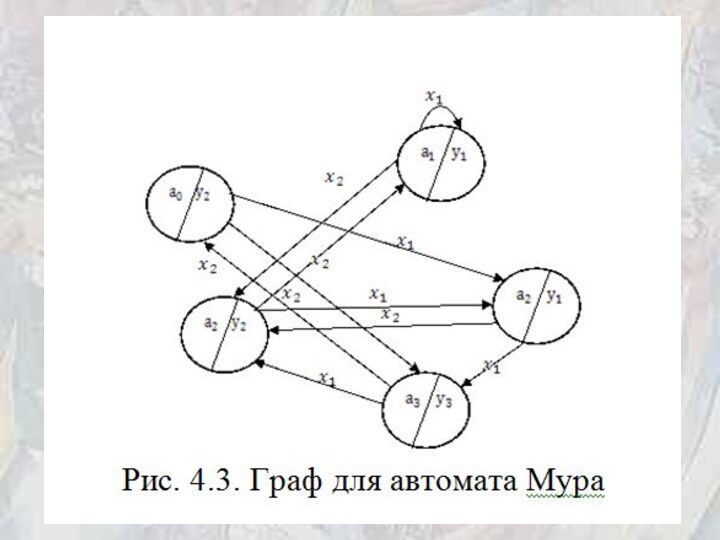
переходам между ними. Две вершины графа ai и as соединяются дугой, направленной от ai к as, если в автомате имеется переход из ai в as, то есть as = d(ai, xj). В автомате Мили (рис. 4.2) дуга отмечается входным сигналом xj, под действием которого происходит этот переход, и выходным сигналом yg, который возникает при переходе. Внутри кружочка, обозначающего вершину графа, записывается состояние автомата. В автомате Мура (рис. 4.3) в вершинах графа кроме состояния автомата отмечается соответствующий выходной сигнал, а дуга отмечается только входным сигналом xj, под действием
которого происходит этот переход.
Слайд 18
Преобразование автомата Мили в автомат Мура
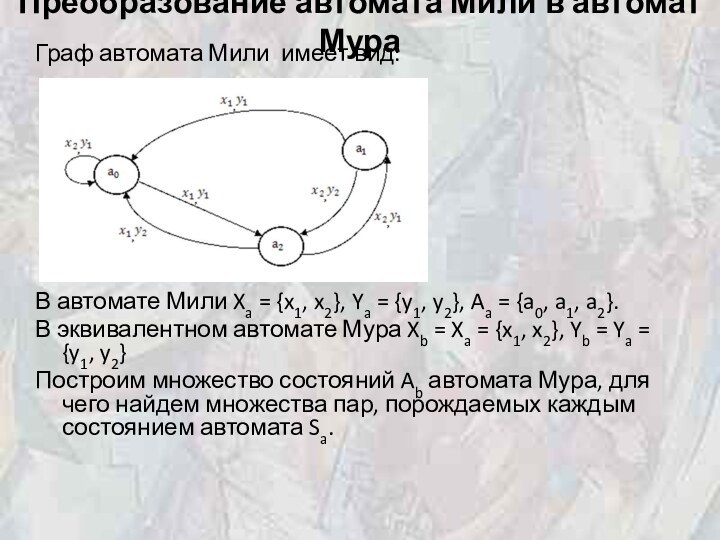
Граф автомата Мили
имеет вид:
В автомате Мили Xa = {x1, x2}, Ya = {y1,
y2}, Aa = {a0, a1, a2}.
В эквивалентном автомате Мура Xb = Xa = {x1, x2}, Yb = Ya = {y1, y2}
Построим множество состояний Ab автомата Мура, для чего найдем множества пар, порождаемых каждым состоянием автомата Sa.
Слайд 19
Состояние Порождаемые пары
a0 {(a0, y1), (a0, y2)} = {b1, b2}
a1 {(a1,
y1)} = {b3}
a2 {(a2, y1), (a2, y2)} = {b4, b5}
Отсюда
имеем множества Ab состояний автомата Мура Ab = {b1, b2, b3, b4, b5}. Для нахождения функции выходов lb с каждым состоянием, представляющим собой пару вида (ai, yg), отождествим выходной сигнал, являющийся вторым элементом этой пары. В результате имеем:
lb(b1) = lb(b3) = lb(b4) = y1; lb(b2) = lb(b5) = y2.
Слайд 20
Построим функцию переходов db. Так как в автомате
Sa из состояния a0 есть переход под действием сигнала x1 в состояние
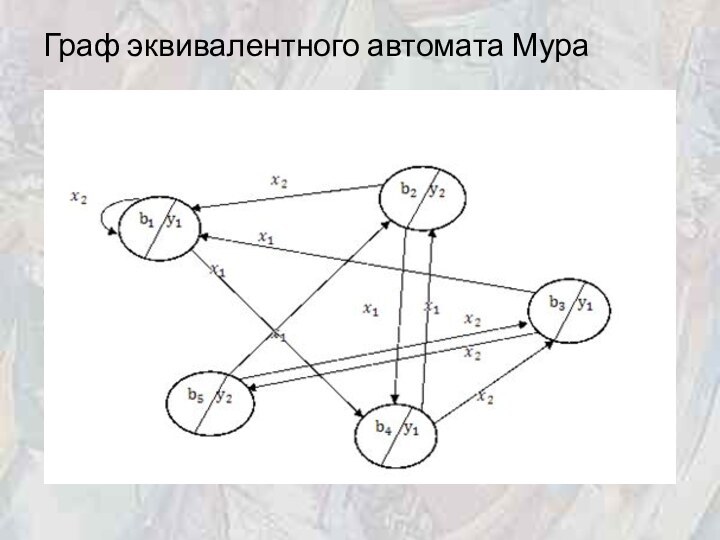
a2 с выдачей y1,то из множества состояний {b1, b2}, порождаемых a0, в автомате Sb должен быть переход в состояние (a2, y1) = b4 под действием сигнала x1. Аналогично, из {b1, b2} под действием x2должен быть переход в (a0, y1) = b1. Из (a1, y1) = b3 под действием x1 переход в (a0, y1) = b1, а под действием x2 – в (a2, y2) = b5. Наконец из состояний {(a2, y1), (a2, y2)} = {b4, b5} под действием x1 в (a0, y2) = b2, а под действием x2 – в (a1, y1) = b3. В результате имеем граф (рис. 7.11) и таблицу переходов эквивалентного автомата Мура.
Слайд 21
Граф эквивалентного автомата Мура
Слайд 22
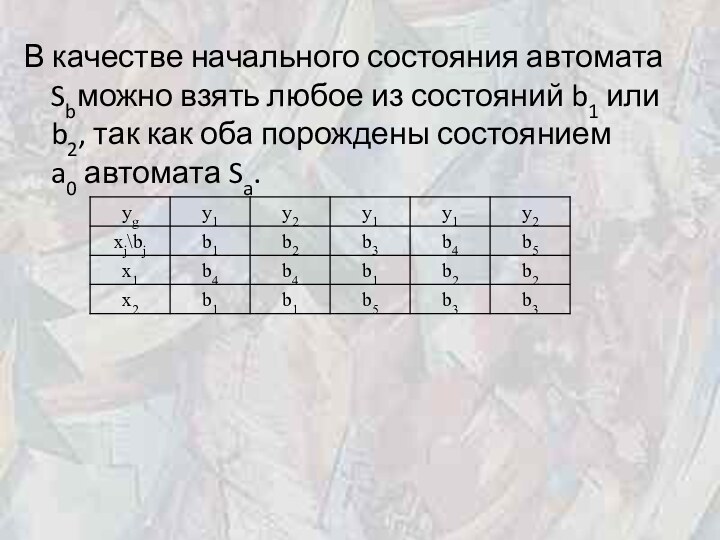
В качестве начального состояния автомата Sbможно взять любое
из состояний b1 или b2, так как оба порождены состоянием
a0 автомата Sa.
Слайд 23
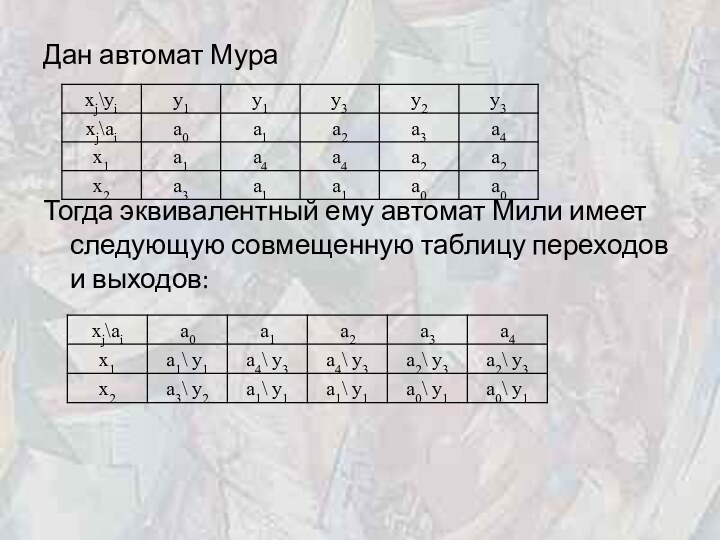
Переход от автомата Мура к автомату Мили
Пусть
дан автомат Мура Sb ={Ab, Xb, Yb, db, lb}. Необходимо
построить эквивалентный ему автомат Мили Sa = {Aa, Xa, Ya, da, la}.
По определению эквивалентности имеем Xa = Xb; Ya = Yb. Кроме того, Aa = Ab, da= db. Остается только построить функцию выходов. Если в автомате Мура db(ai, xj) = as, а lb(as) = yg, то в автомате Мили la(ai, xj) = yg. Другими словами: l(ai, xj) = lb(db(ai, xj)). Таким
образом, таблица переходов автоматов Мили и Мура совпадают. А таблица выходов эквивалентного автомата Мили строится так, что в каждую клетку таблицы записывается выходной сигнал, которым отмечено состояние, расположенное в данной клетке.