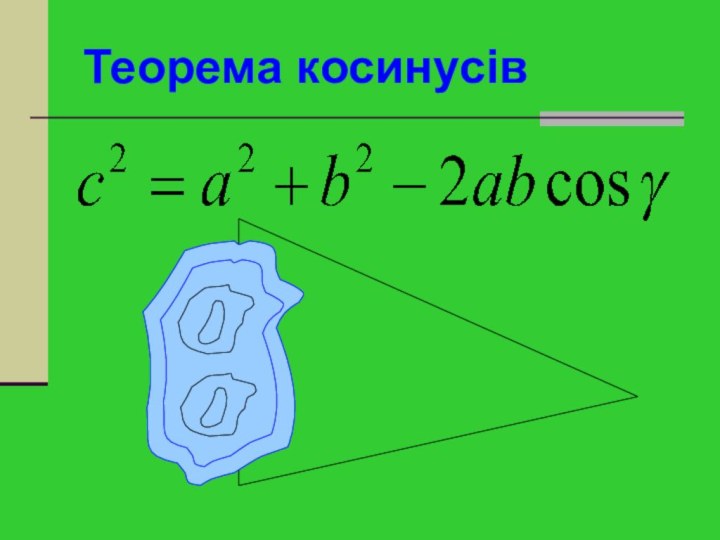
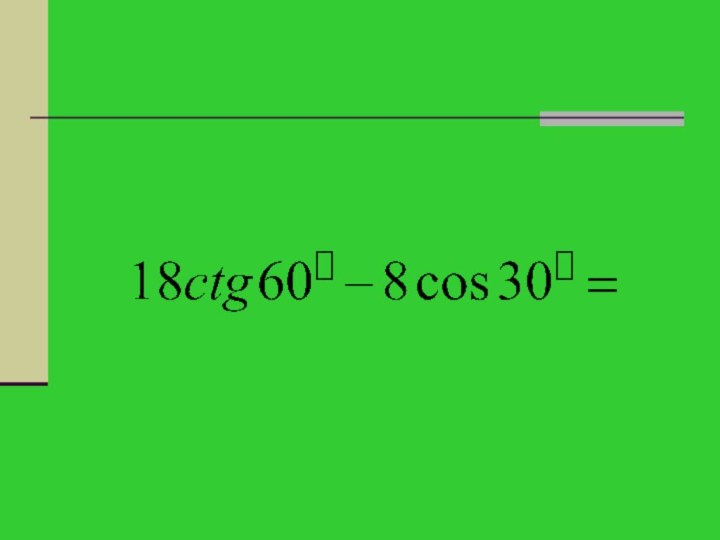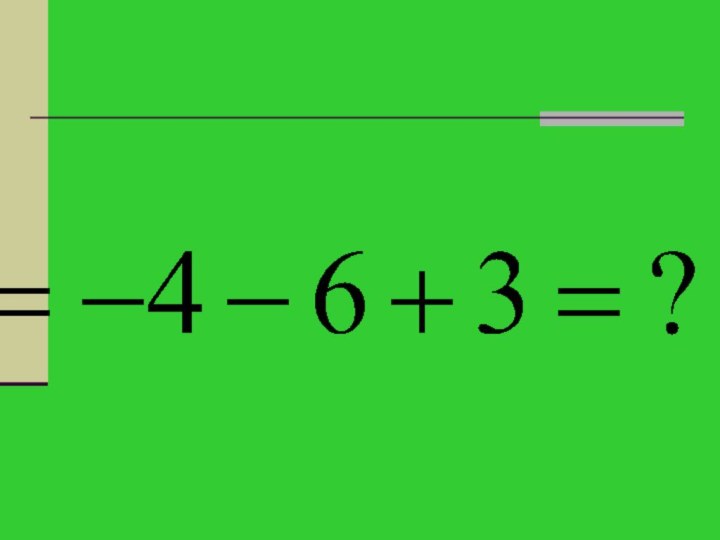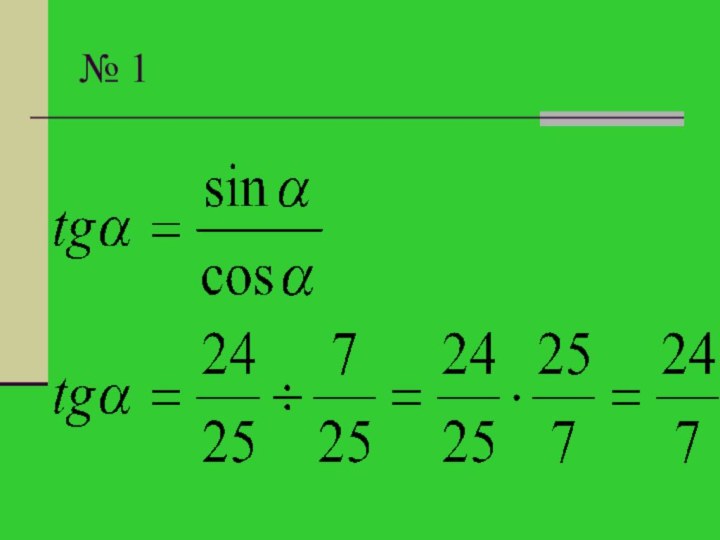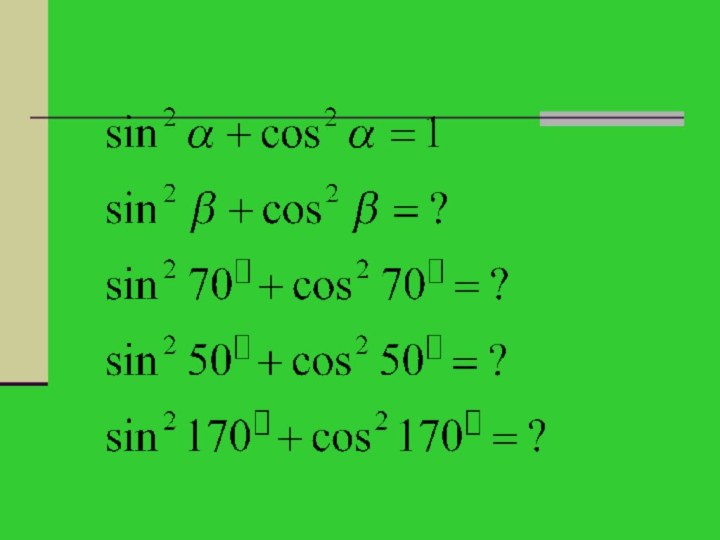Слайд 2
«Велика книга природи може
бути прочитана
тільки тими,
хто знає мову,
на якій вона
написана,
і ця мова –
математика.»
Галілео Галілей
(1564 – 1642)
Слайд 3
План заняття
Історична довідка.
Періодичні процеси.
Тригонометричні функції числового аргументу.
Основні тригонометричні
тотожності.
Коментування задач за допомогою комп'ютера.
Розв'язування вправ:
- усно;
- колективно;
- письмово.
Тестовий
контроль.
Підсумок заняття.
Слайд 4
Мета
узагальнити і систематизувати знання студентів про основні властивості
тригонометричних функцій,
формувати навички та вміння обчислювати значення тригонометричних
функцій,
тотожно перетворювати тригонометричні вирази за допомогою співвідношень між тригонометричними функціями одного аргументу;
Слайд 6
Історична довідка
Термін “тригонометрія” походить від грецьких слів “тригон”
– трикутник і “метризис” – вимірюю та означає у
перекладі “вимірювання трикутників”, був запропонований у 1595 р.
німецьким математиком
Варфоломеєм П і т і с к о м
(1561 - 1613).
Слайд 7
Історична довідка
Тригонометрія, як астрономія і географія,
зародилася та розвивалась у Вавилоні, Єгипті, Китаї, Індії та
інших країнах.
Слайд 8
Значного розвитку тригонометрія як частина астрономії
набула у Стародавній Греції в роботах великих математиків Євклида,
Архимеда, Апполонія Пергського.
Архимед
Євклид
Апполоній
Пергський
Слайд 9
Принципіальне значення мало складання Клавдієм Птолемеєм
першої таблиці синусів (довгий час вона називалась таблицею хорд).
З’явився практичний засіб розв’язування прикладних задач.
Слайд 10
Історична довідка
Греки першими почали розв’язувати прямокутні
трикутники, у зв’язку з чим склали тригонометричні таблиці.
Слайд 11
За допомогою тригонометрії
давньовавилонські вчені виконували
розрахунки:
передбачення сонячних та місячних затемнень;
містознаходження судна.
Слайд 12
Древньогрецький астрономом, математик
Г і п п
а р х
(біля 150 р. до н. е.):
- склав перші тригонометричні таблиці;
- увів географічні координати – широту і довготу;
- визначив відстань від Землі до Місяця.
Слайд 13
Тригонометричні таблиці високої точності було складено у ХV
ст. середньоазіатським ученим а
л – К а ш і (XIV – XV ст.)
та німецьким астрономом і математиком Р е г і о м о н т а н о м
(1436 - 1476).
Слайд 14
У Росії перші тригонометричні таблиці були
видані у 1703 році, в складанні яких брав участь
Леонтій Пилипович
М а г н и ц ь к и й (1669 - 1739).
Слайд 15
Історична довідка
Вчення про тригонометричні функції почало
розвиватися ще у ІV – V ст. у працях
індійських вчених. Термін “sinus” хоч і було введено латинською мовою у ХІІ ст., та переклали його з індійської “архадживе”, що означає “половину хорди”.
Слайд 16
Історична довідка
Термін “косинус” походить від скорочення двох слів
“sinus complementi” (синус доповнення sin(90º-х)), які вживав Регіомонтан.
Слайд 17
Історична довідка
У ІХ – Х ст. середньоазіатські вчені
ввели поняття тангенса, котангенса.
м (1561 - 1656).
Латинське слово “tangens”
означає “той, що дотикається”.
Термін “котангенс” походить, як і
косинус, від словосполучення
“tangens complementi”.
Термін “тангенс” було введено у 1583р. німецьким математиком
Слайд 19
Сучасного вигляду вчення про тригонометричні функції набуло в
працях
Л е о н а
р д а Е й л е р а (1707 - 1783)
Леонардо Ейлер:
- швейцарець за походженням;
- працював у Петербурзькій
Академії наук;
- вивчав математику, фізику,
астрономію;
розглядав тригонометрію як
науку про тригонометричні функції.
Слайд 20
Леонардо Ейлер:
- уперше виклав відомості про знаки
тригонометричних
функцій;
- дослідив їх області визначення;
- ввів позначення функцій sin x, cos x,
tg x, ctgх;
Слайд 21
Леонардо Ейлер:
– автор ряду тригонометричних формул;
- дав сучасне
визначення тригонометричних функцій;
- вказав на зв’язок цих функцій з
показниковими функціями;
- залишив понад 800 робіт, довів багато теорем, які стали класичними теоремами.
Слайд 22
Титульний лист та перша
сторінка книги Леонардо Ейлера «Введение в анализ бесконечных». 1748
р.
Слайд 23
Синусоїда
Зима за літом, ніч – за днем,
плюс змінюється мінусом,
все у природі і в людей
йде за законом синуса.
Слайд 24
Ряди везінь і невезінь
то зверху, то насподі ми.
Із березоля в березіль
виходимо й приходимо.
Слайд 25
Гріхопадіння й каяття,
і нищення, і творення.
Проста гармонія буття:
повторення й повторення.
Слайд 26
То вверх крокуємо, то вниз,
удачі
– за невдачами;
по синусоїді кудись
всі пливемо неначе ми.
Слайд 29
Сімейство троянд Гвідо Гранді
Одного разу італійський геометр Гвідо
Гранді (1671-1742) створив троянди. Ні, зовсім не ті рослини,
які відомі всім.
Троянди Гвідо Гранді милують правильними плавкими лініями.
Їх обриси не примха природи –вони передумовлені спеціально підібраними математичними залежностями.
Слайд 30
«Сімейство троянд Гвідо Гранді можна описати рівнянням у
полярних координатах:
де a і k –деякі сталі
(постійні). На зображені ці криві при різних значеннях параметру k.
Слайд 31
На малюнку 1 зображені ці криві при різних
значеннях параметра k
Слайд 32
Зачарований результатами Гранді,
німецький геометр ХІХ ст.
Хабеніхт також
вирішив
зайнятися
математичним
«рослинознавством».
Слайд 33
Хабеніхт шляхом різноманітних дослідів «зростив» чудові експонати (мал.2).
У наші дні подібні досліди зручно проводити, маючи під
рукою персональний комп’ютер.
Слайд 34
В огромном саду геометрии каждый найдёт букет себе
Слайд 35
Періодичні процеси
Новий клас функцій – тригонометричні функції.
Вони існують
для опису різних періодичних процесів.
З ситуаціями , які
повторюються, людина зустрічається скрізь.
Слайд 36
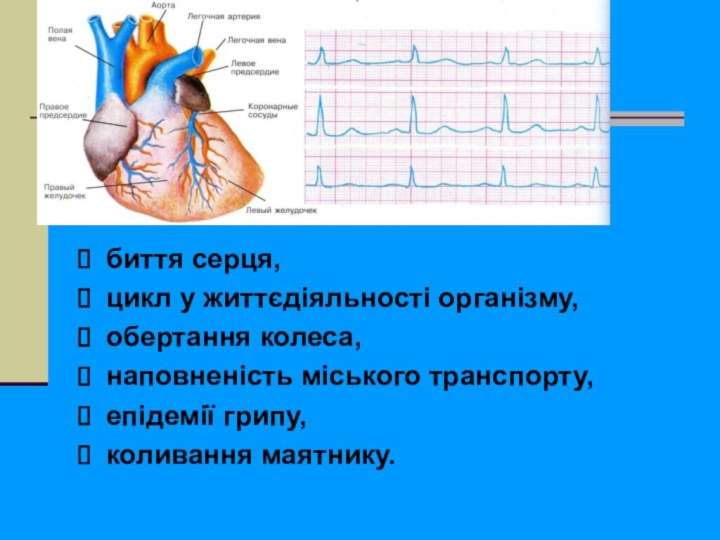
Людина давно помітила періодичну відновлюваність явищ
Його життя супроводжують
різні астрономічні явища:
схід і захід Сонця,
зміщення фаз Місяця,
чергування пір року,
положення зірок на небі,
затемнення і рухи планет,
морські приливи і відливи,
Слайд 37
биття серця,
цикл у життєдіяльності організму,
обертання колеса,
наповненість міського транспорту,
епідемії грипу,
коливання маятнику.
Слайд 38
Відкриваючи вранці газету, ми часто читаємо повідомлення про
черговий запуск штучного супутника Землі. Зазвичай у повідомленні вказують
найменшу і найбільшу відстань супутника від поверхні Землі і період його обертань. Якщо сказано, що період обертання супутника складає 92 хвилини, то ми розуміємо, що його положення відносно Землі в якийсь момент часу і через кожні 92 хвилин з цього моменту буде однаковим. Так ми приходимо до поняття періодичної функції.
Слайд 42
Безконтактний
лазерний
вимирювач
відстані між
двома точками
(Red Point Measure)
Слайд 43
Глобальна Навігаційнна Система (GPS)
Для визначення широти та довжини
приймача необхідно, як мінімум, приймати сигнали від трьох супутників.
Прийом сигналу від четвертого супутника позволяє визначити висоту об’єкта над поверхнею.
Слайд 44
Комп’ютер приймача розв’язує чотири рівняння з чотирма невідомими
до тих пір, поки не знайде рішення, яке проводить
усі кола через одну точку.
Слайд 45
Геоцентрична система світу
1 градус –
слід Сонця
Слайд 46
Геліоцентрична система світу Коперника
Слайд 48
Додавання двох гармонічних коливань
Слайд 50
Тригонометрична форма запису комплексного числа
Слайд 53
Об'єм циліндра можна обчислити за допомогою формули:
Цю формулу можна спростити?
Слайд 54
Для налаштування фрезеровального станка на фрезерування муфти робітникові
рекомендують використувати формулу
Слайд 55
Рух поршня двигуна машини визначається за формулою:
Де l
– довжина двигуна,
R - радіус вала,
φ -
кут руху.
Визначити рух поршня при φ=π/2, якщо R=10см, l =32см.
Слайд 57
рад = 180град.
1 радіан наближено
дорівнює
57 градусам.
Леонард Эйлер
(1707-1783).
Слайд 58
ТРИГОНОМЕТРІЯ
Сфери
Астрономія
Геодезія
Картографія
Механіка
Оптика
Акустика
……………..
……………..
………………
застосування
Будівництво
Архитектура
Дизайн
Навигація
Медицина
Музика
Спорт
…………………
…………………
Слайд 60
Дайте визначення (1б)
а) косинуса, синуса, тангенса, гострого кута
в прямокутному трикутнику
В
а с
С А
Слайд 61
Дайте визначення (1б)
б) косинуса, синуса, тангенса числового аргументу
А (x,y)
Y
відношення;
Х - абсциса;
У - ордината;
R - радіус.
X
Слайд 62
За якими формулами переводять градусну міру кута в
радіанну та навпаки?
Слайд 63
За якими формулами переводять градусну міру кута в
радіанну та навпаки?
π рад = 180˚
1˚ = рад
1 рад = 90˚ = =
1 рад = 57˚ 60˚ = =
Слайд 64
Які з тригонометричних функцій
являються парними, а які
непарними?
cos (- α) =
sin (- α)
=
tg (- α) =
ctg (- α) =
Y
Pα
X
P-α
Слайд 65
Які з тригонометричних функцій являються парними, а які
непарними?
cos (- α) = cos α
sin
(- α) = - sin α
tg (- α) = - tg α
ctg (- α) = - ctg α
Y
Pα
X
P-α
Слайд 66
8. Згадаємо знаки тригонометричних функцій у координатних
Слайд 67
Згадаємо знаки тригонометричних функцій у координатних чвертях (1б)
Sinα
Слайд 68
Згадаємо знаки тригонометричних функцій у координатних чвертях
y
x
Слайд 69
Згадаємо знаки тригонометричних функцій у координатних чвертях
tgα, ctgα
y
x
Слайд 70
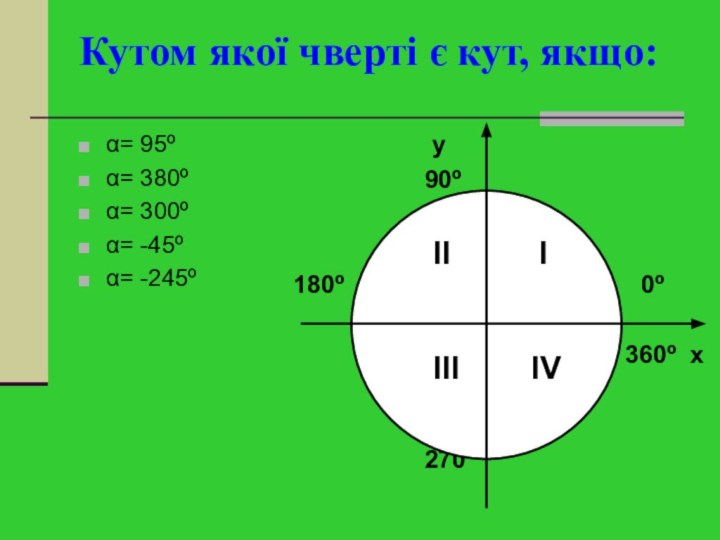
Кутом якої чверті є кут, якщо:
α= 95º
α=
380º
α= 300º
α= -45º
α= -245º
y
90º
180º 0º
360º x
270º
Слайд 71
Яке число являється найменшим позитивним періодом
а)
синуса та косинуса
б) тангенса та
котангенса.
Слайд 72
Яке число являється найменшим позитивним періодом
а)
синуса та косинуса
cos (α ± 2π)
= cos α T= 2π
sin (α ± 2π) = sin α
cos (α ± 360º) = cos α T= 360º
sin (α ±360º) = sin α
б) тангенса та котангенса.
tg (α ± π) = tg α T= π
ctg (α ± π) = ctg α T= 180º
Слайд 93
Основні
тригонометричні
тотожності
Слайд 94
Основні тригонометричні тотожності
Слайд 95
Основні тригонометричні тотожності
Слайд 96
Основні тригонометричні тотожності
Слайд 103
Разом (коментар)
Відомо, що
. Знайти cosα.
. Знайти sinα.
αєІІ чверті.
Слайд 110
Спростити вирази
sinα + sinα =?
cosα + cosα =?
sinα -
sinα =? cosα - cosα =?
sinα sinα =?
cosα cosα =?
Слайд 116
Чи можуть синус та косинус одного й того
ж числа бути рівними відповідно:
Слайд 117
Чи можуть тангенс та котангенс одного й того
ж числа бути рівними відповідно:
Слайд 122
Спростити.
№2 Відповідь студентів. (2бали)
Слайд 127
Спростити у дошки. Відповіді студентів. (3 бали)
Слайд 136
Спростити.
Записати у зошиті. (3бали)
Слайд 145
Спростити.
Усний коментар.(2бали) :
Слайд 148
Довести тотожність: (3 бали)
Відповідь студента у дошки.
Слайд 149
Довести тотожність: (3 бали)
Відповідь студента у екрана.
Слайд 150
Довести тотожність: (3 бали)
Відповідь студента у дошки.
Слайд 151
Довести тотожність: (3 бали)
(самостійно у зошитах)
Слайд 152
Довести тотожність: (3 бали)
Відповідь
Слайд 153
Довести тотожність: (3 бали)
Відповідь
Слайд 154
№3. Довести тотожність: (5 бал.)
Відповідь студента у дошки.
Слайд 159
Довести тотожність: (5 бал.)
Відповідь студента у дошки.
Слайд 160
Довести тотожність: (5 бал.)
Відповідь студента у екрана.
Слайд 161
Довести тотожність: (5 бал.)
Відповідь студента у екрана.
Слайд 162
Довести тотожність: (5 бал.)
Відповідь студента у екрана.
Слайд 163
Довести тотожність: (5 бал.)
Відповідь студента у екрана.
Слайд 164
Довести тотожність: (5 бал.)
Відповідь студента у екрана.
Слайд 165
Довести тотожність: (5 бал.)
Відповідь студента у екрана.
Слайд 166
Довести тотожність: (5 бал.)
Відповідь студента у екрана.
Слайд 167
Рух поршня двигуна машини визначається за формулою (Робота
у дошки (4б)).
де l – довжина шатуна,
R -
радіус вала,
φ - кут руху.
Визначити рух поршня при φ=π/2, якщо R=10см, l=25см.
Слайд 168
Рух поршня двигуна машини визначається за формулою:
Слайд 169
Рух поршня двигуна машини визначається за формулою:
Слайд 170
Рух поршня двигуна машини визначається за формулою:
Слайд 171
Кут нахилу всіх ескалаторів киівського
метро дорівнює 30 градусам. Зная це, кількість ламп
на эскалаторі і наближену відстань між лампами (6 м), можна обчислити наближену глибину закладання станції.
«Арсенальна»- сама глубока в світі станція метро
35 відрізків
.6 метрів =210 метров –довжина сходів.
210 : 2 = 105,5 (м) – глубина закладання станції.
(Офіційні дані – 105,5 м)
«Крещатик» - 22 відрізка.
3. «Майдан» - 25 відрізків.
Слайд 173
Розв’язування (2 бали)
2.«Крещатик»
22 відрізка .6 метрів
=132 метра –довжина сходів.
132 : 2 = 66
(м) – глибина закладання станції.
(Офіційні дані – 67 м)
3.«Майдан»
25 відрізків .6 метрів =150метрів –довжина сходів.
150 : 2 = 75 (м) – глибина закладання станції.
(Офіційні дані – 75 м)
Слайд 175
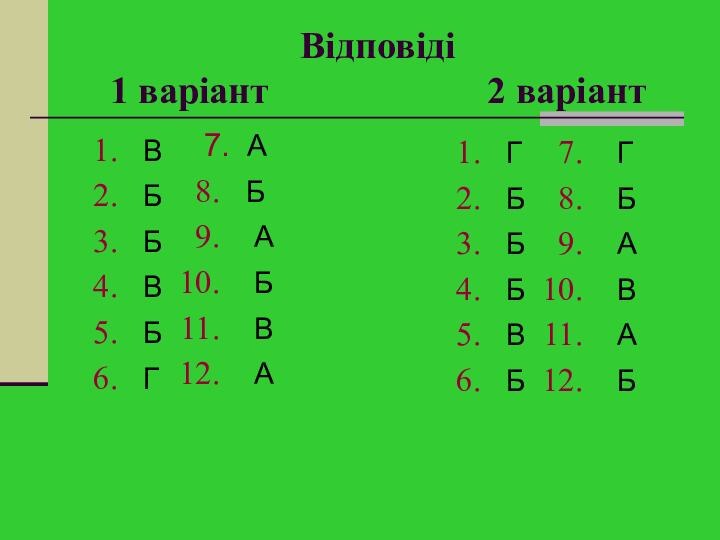
Відповіді
1 варіант
2 варіант
В
Б
Б
В
Б
Г
7. А
Б
А
Б
В
А
Г
Б
Б
Б
В
Б
Г
Б
А
В
А
Б
Слайд 176
Домашнє завдання:
1. Повторити формули.
2. Виконати домашнє завдання (індивідуальну
картку) на окремих листах.
3. Робота з опорним конспектом.
Слайд 179
Математика... выявляет порядок, симметрию и определённость, а
это — важнейшие виды прекрасного.
Аристотель