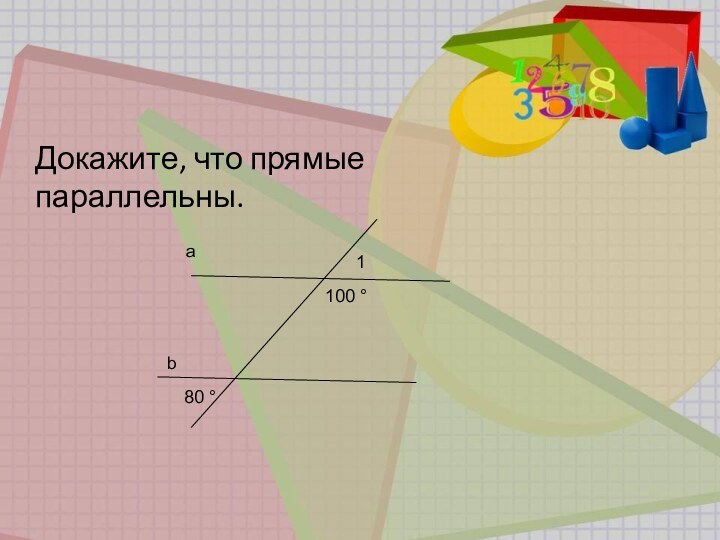
пересечения двух прямых
секущей; изучить признаки параллельности прямых;
формирование
умений анализировать изученный материал и навыков применения его для решения задач; показать
значимость изучаемых понятий; закрепить навыков
решения задач на применение признаков параллельности
прямых;
развитие познавательной активности и самостоятельности
получения знаний;
воспитание интереса к предмету, самостоятельности.