- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Материалы к занятию. Алгебра комбинаторика.
Содержание
- 2. Комбинаторика для великих комбинаторов
- 3. Кого из литературных героев называют Великим комбинатором?
- 4. Остап Бендер — это главный герой романов
- 5. Оста́п Бе́ндер — главный герой романов Ильи Ильфа и Евгения Петрова «Двенадцать
- 6. Почему Остапа Бендера называют Великим комбинатором?
- 7. КомбинаторикаТермин «комбинаторика» был введён Лейбницем в 1666
- 8. Перестановки и размещения
- 9. Задача 1. Милиционер плохо запомнил имя преступника,
- 10. ОстапСулейманБертаМарияБендерБейОстапСулейманМарияБендерБейОстапМарияБендерБейОстапМарияБейОстапБейОстап
- 12. Способы подсчета количества вариантовМетод организованного перебораТаблица (удобно
- 13. Например, организованный переборВ задаче о подбрасывании монеты(О,Р,О)(О,О,О)(О,О,Р)(Р,О,О)И т.д.
- 14. По командам:Яблоко, апельсин, груша и банан лежат
- 16. На доске обе команды на скорость таблицейВ
- 17. Задача 1810 рукопожатий
- 18. Задача 22Начертить граф, который соответствует заданию .РешениеЗадачи, решаемыес помощью графов
- 19. Задача 21Из каждой пары чисел 63, 9,
- 20. Задача 2 (размещения). Десять стульев были проданы
- 22. Сколько стратегий поиска стульев (порядка поиска стульев)
- 23. Театр КолумбаЭллочкаГр. Садово-Спасское«Станок»Кв. у Чистых прудовВокзалТеатр КолумбаЭллочка«Станок»Кв. у Чистых прудовВокзал
- 24. Ответ к задаче 2- вариантов стратегий просчитал Остап Бендер мгновенно.
- 25. Перестановки - комбинации из n элементов, отличающиеся
- 26. Сравнительная таблица подсчета числа перестановок и размещений
- 27. Сочетания
- 28. Задача 3: Членами подпольной организации
- 29. СочетанияКомбинации по m различных элементов, выбранных их
- 30. Задача 3: Членами подпольной организации
- 32. Ответ к задаче 3:
- 33. ПерестановкиФормула для подсчета количества всевозможных перестановок:
- 34. РазмещенияФормула для нахождения количества размещений различных m
- 35. Сочетания Формула для нахождения количества сочетаний m элементов из n:
- 36. На занятии мы узнали Для того,
- 37. Скачать презентацию
- 38. Похожие презентации

































Слайд 4 Остап Бендер — это главный герой романов Ильи
Ильфа и Евгения Петрова «Двенадцать стульев» и «Золотой телёнок».
Слайд 5 Оста́п Бе́ндер — главный герой романов Ильи Ильфа и Евгения Петрова «Двенадцать стульев»
и «Золотой телёнок», «великий комбинатор», «идейный борец за денежные знаки»,
знавший «четыреста сравнительно честных способов отъёма (увода) денег». Один из самых популярных героев плутовского романа в отечественной литературе.Сам Бендер представляется как Остап-Сулейман-Берта-Мария-Бендер-бей (в «Двенадцати стульях») и Бендер-Задунайский (в «Золотом телёнке»). В романе «Золотой телёнок» Бендера именуют Остап Ибрагимович.
Слайд 7
Комбинаторика
Термин «комбинаторика» был введён Лейбницем в 1666 году.
Он
происходит от латинского слова «combina», что в переводе
на русский означает – «сочетать», «соединять».Комбинаторика - раздел математики, описывающий методы быстрого подсчета количества различных комбинаций заданных объектов.
Слайд 9
Задача 1.
Милиционер плохо запомнил имя преступника, но
помнит, что в нем есть
Мария, Сулейман, Остап, Берта,
Бей и Бендер. Сколько имен должен написать милиционер, чтобы среди них обязательно оказалось имя «преступника»?
Слайд 10
Остап
Сулейман
Берта
Мария
Бендер
Бей
Остап
Сулейман
Мария
Бендер
Бей
Остап
Мария
Бендер
Бей
Остап
Мария
Бей
Остап
Бей
Остап
Слайд 12
Способы подсчета количества вариантов
Метод организованного перебора
Таблица (удобно для
выбора двух значений из нескольких возможных)
Дерево вариантов
Граф
Формулы для подсчета
количества размещений, перестановок и сочетаний
Слайд 13
Например,
организованный перебор
В задаче о подбрасывании монеты
(О,Р,О)
(О,О,О)
(О,О,Р)
(Р,О,О)
И т.д.
Слайд 14
По командам:
Яблоко, апельсин, груша и банан лежат на
столе в ряд.
Апельсин не в начале и не в
конце этого ряда.Стоя лицом к этому ряду, можно увидеть, что апельсин - справа от банана (но не обязательно рядом с ним).
Сколько разных вариантов расположения фруктов может быть ?
Окно в комнате Кости имеет прямоугольную форму и разделено на 3х3 маленьких секций.
Костя хочет покрасить две секции желтой краской. Но он хочет покрасить их так, чтобы окно смотрелось одинаковым, если смотреть на него снаружи или изнутри.
Сколько всего способов покрасить свое окно есть у Кости ?
Слайд 16
На доске обе команды на скорость таблицей
В одной
деревне по сложившейся традиции мужчин называют каким-либо из следующих
имен: Иван, Петр, Василий и Михаил. Проживают в этой деревне 15 мужчин с разными именами. Может ли оказаться так, что в деревне нет мужчин с одинаковым именем и отчеством?Решение
Задачи, решаемые
с помощью таблиц
Слайд 18
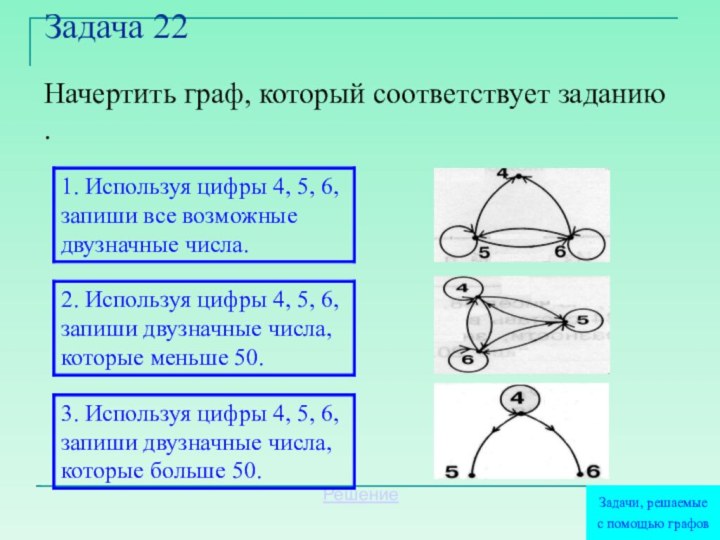
Задача 22
Начертить граф, который соответствует заданию .
Решение
Задачи, решаемые
с
помощью графов
Слайд 19
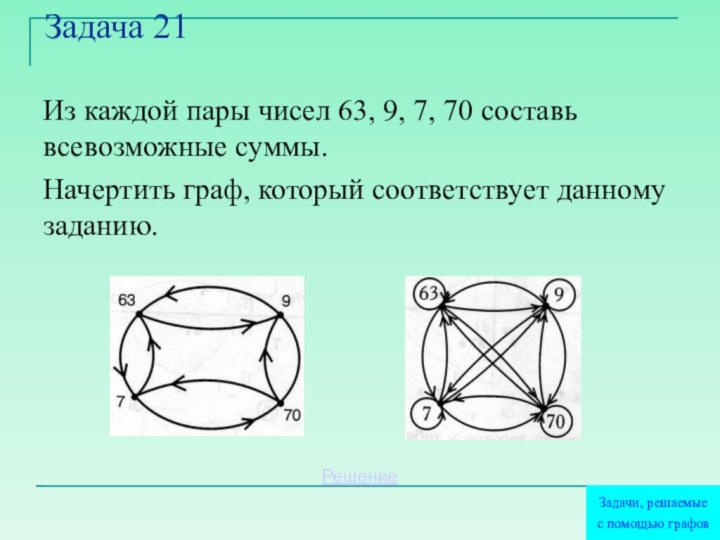
Задача 21
Из каждой пары чисел 63, 9, 7,
70 составь всевозможные суммы.
Начертить граф, который соответствует данному
заданию.Решение
Задачи, решаемые
с помощью графов
Слайд 20
Задача 2 (размещения).
Десять стульев были проданы с
аукциона в розницу. Остап Бендер отправил по их следу
беспризорников. Он узнал:
Слайд 22
Сколько стратегий поиска стульев (порядка поиска стульев) Остап
Бендер смог просчитать мгновенно, если за один миг он
просчитывал все варианты развития событий на два шага вперед?
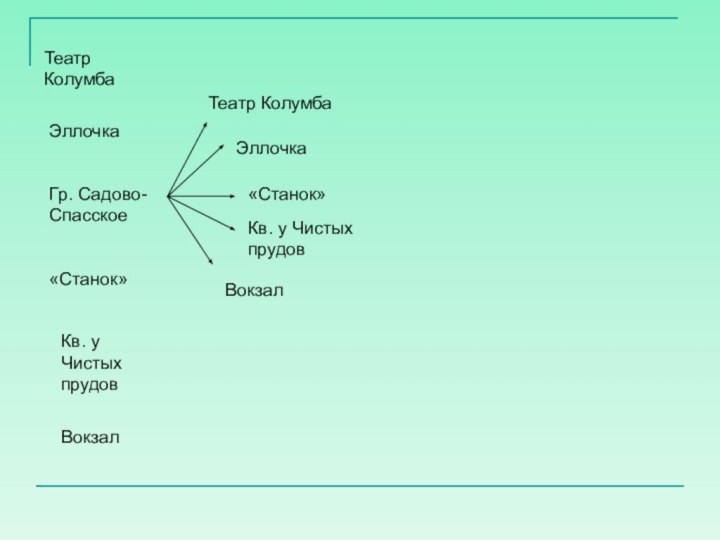
Слайд 23
Театр Колумба
Эллочка
Гр. Садово-Спасское
«Станок»
Кв. у Чистых прудов
Вокзал
Театр Колумба
Эллочка
«Станок»
Кв. у
Чистых прудов
Вокзал
Слайд 25 Перестановки - комбинации из n элементов, отличающиеся друг
от друга только порядком их расположения
Найти все перестановки
цифр числа 1542 и 8362 ( на баллы) и их количествоРазмещения - комбинации по m различных элементов, выбранных из множества, содержащего n элементов, которые отличаются друг от друга не только порядком, но и составом элементов
Пример. Всевозможные размещения из трех элементов 123 и 561 по два элемента:12, 13, 21, 23, 31, 32.
А с повторениями + 11, 22, 33
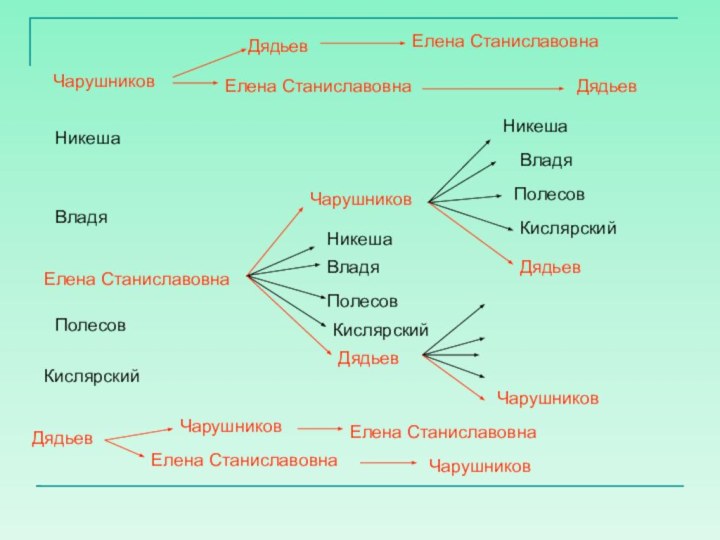
Слайд 28 Задача 3: Членами подпольной организации были 7
человек: 1. Чарушников, 2. Никеша, 3. Владя, 4. Полесов, 5.
Елена Станиславовна, 6. Кислярский, 7. Дядьев. Остап устраивал собрания подпольщиков. На них он приглашал по 3 члена союза. На каждом собрании Остап Бендер зарабатывал по 1 тысяче рублей.
Сколько денег Остап Бендер сможет собрать с подпольщиков, если будет приглашать на собрания каждый раз новый состав членов подпольной организации?
Слайд 29
Сочетания
Комбинации по m различных элементов, выбранных их множества
n данных элементов, которые отличаются друг от друга только
составом элементов называются сочетаниями
Слайд 30 Задача 3: Членами подпольной организации были 7
человек: 1. Чарушников, 2. Никеша, 3. Владя, 4. Полесов, 5.
Елена Станиславовна, 6. Кислярский, 7. Дядьев. Остап устраивал собрания подпольщиков. На них он приглашал по 3 члена союза. На каждом собрании Остап Бендер зарабатывал по 1 тысяче рублей.
Слайд 33
Перестановки
Формула для подсчета количества всевозможных перестановок:
Слово «факториал» в переводе с латинского означает «производящий действие».
Перестановками называют комбинации из n элементов, отличающиеся друг от друга только порядком их расположения
Слайд 34
Размещения
Формула для нахождения количества размещений различных m элементов
из n:
Размещениями называются комбинации по m различных элементов, выбранных
из множества, содержащего n элементов, которые отличаются друг от друга не только порядком, но и составом элементов.
Слайд 36
На занятии мы узнали
Для того, чтобы
стать Великим комбинатором надо уметь быстро просчитывать все варианты
развития событий.В этом нам помогают формулы:
1.
2.
3.
- Формула подсчета количества сочетаний
- формула подсчета количества размещений
- Формула подсчета количества перестановок





























