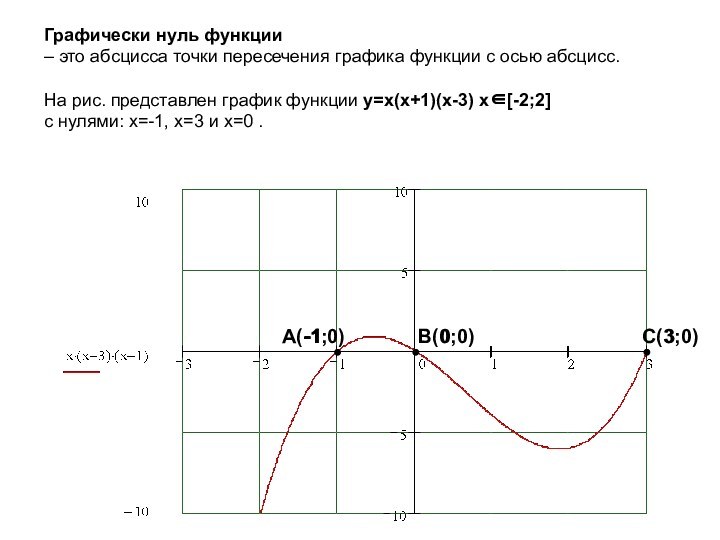
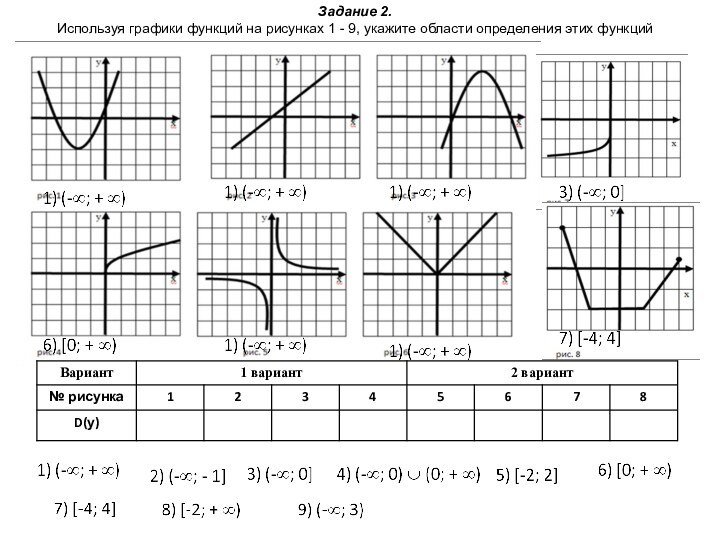
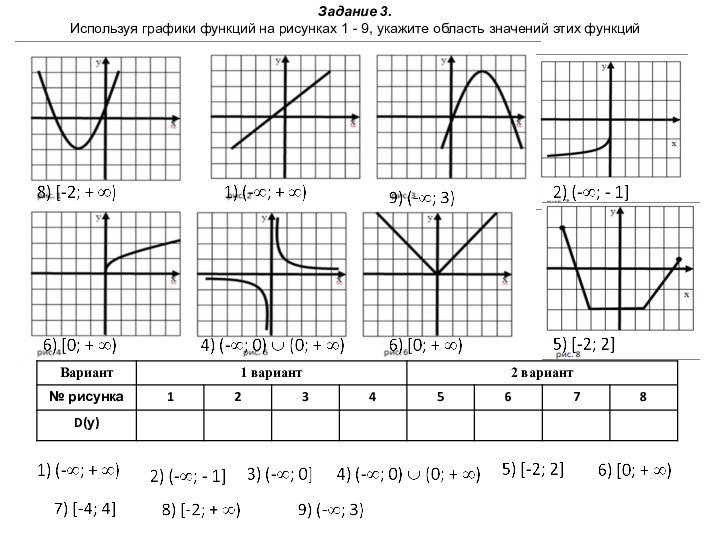
независимой переменной соответствует единственное значение другой зависимой переменной.
Переменная, значение
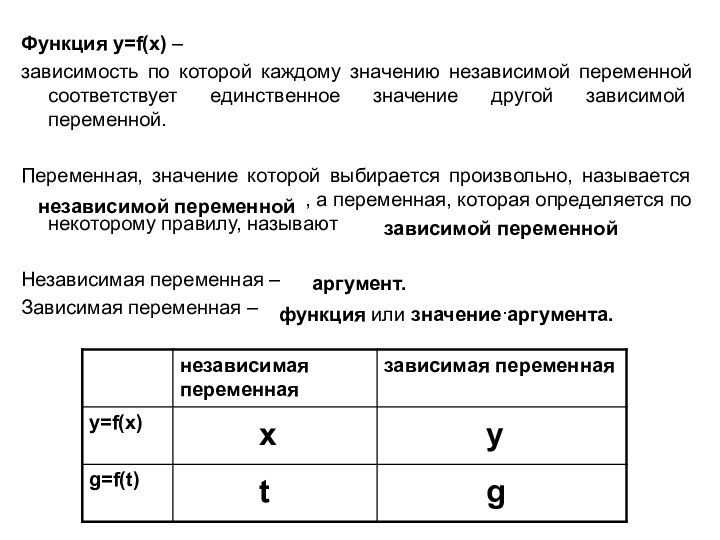
которой выбирается произвольно, называется независимой переменной, а переменная, которая определяется по некоторому правилу, называют зависимой переменной.Независимая переменная –
Зависимая переменная – .
аргумент.
функция или значение аргумента.
у
g
x
t
независимой переменной
зависимой переменной

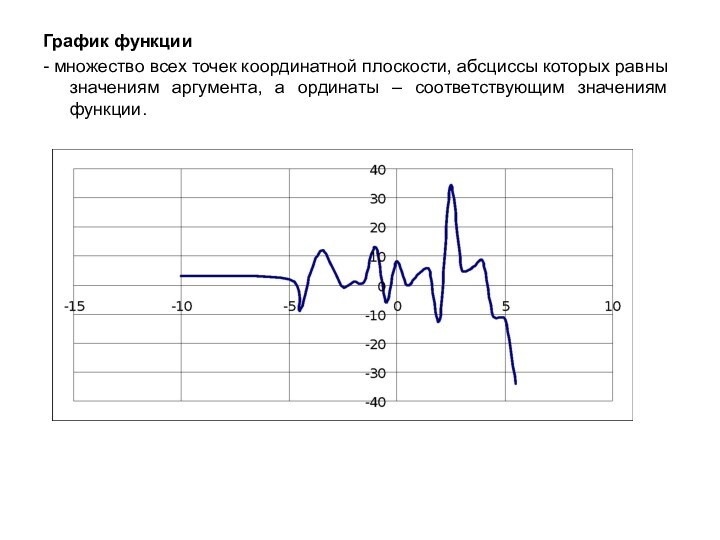





![Функция (7 класс) 4-4D(f) x[-4;4]Найдите область определения функции](/img/tmb/12/1186633/666310f899d9b43f538ff2a6845a825f-720x.jpg)

![Функция (7 класс) -2 2E(f) x[-2;2]Найдите область значения функции](/img/tmb/12/1186633/fe86a9f6a066816bdb2ce2507b94f218-720x.jpg)