- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему: Первообразная и интеграл (11кл.)
Содержание
- 2. Открытие дифференциального и интегрального исчислений невозможно было бы без фантазии. Лейбниц.
- 3. Цель урока:
- 4. План урока1.разминка2.мозаика фактов3.вычисление интегралов3.дальше,дальше…4.истинны ли равенства?5.кроссворд6.выполнить тест7.подведение итогов урокаХОД УРОКА
- 5. Разминка! I.
- 6. II
- 7. Мозаика фактов. Термин «Первообразная» ввёл в 1797
- 8. Вычислить интегралы.
- 9. Дальше, дальше…1. Запишите с помощью интеграла площадь
- 10. 3. Истинны ли равенства :; б) ; в) ;г) ;д) ;е) ?
- 11. 1. Как называется функция F(x)? 2. Что
- 12. Изобразить криволинейную трапецию, ограниченную:а) графиком функции
- 13. Задание 1.Для функции f(х)=Найти первообразную, график которойпроходит
- 14. Задание 2С помощью формулы Ньютона-Лейбница вычисляют:
- 15. Задание 3Найти площадь фигуры, ограниченной осью ОХ
- 16. Подведение итогов урока
- 17. I. Разминка -8 баллов. Задание 1
- 18. IV. Кроссворд – 12 баллов1) первообразная
- 19. Б; В; А.VI. Тест – 3 балла
- 20. Результаты:
- 21. Скачать презентацию
- 22. Похожие презентации
Открытие дифференциального и интегрального исчислений невозможно было бы без фантазии. Лейбниц.
















Слайд 3 Цель урока: Закрепление изученного материала; способствовать учащимся реализовать полученные
знания при выполнении заданий различного уровня.
цель урока
Слайд 4
План урока
1.разминка
2.мозаика фактов
3.вычисление интегралов
3.дальше,дальше…
4.истинны ли равенства?
5.кроссворд
6.выполнить тест
7.подведение итогов
урока
ХОД УРОКА
Слайд 5
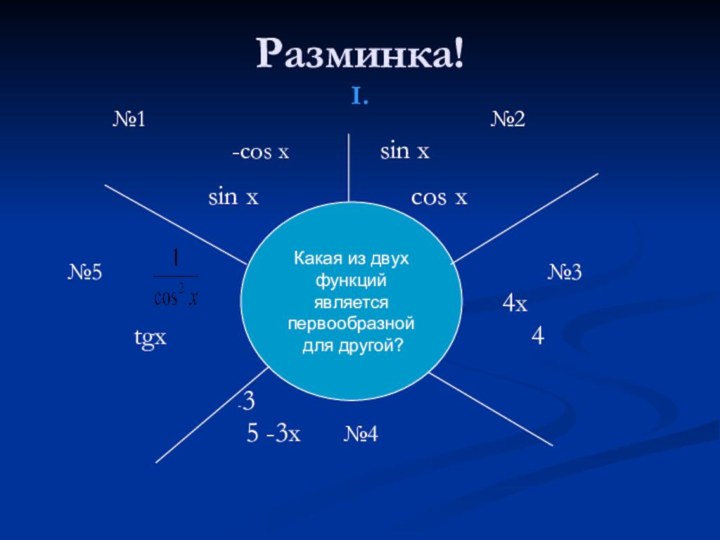
Разминка!
I.
№1 №2
-cos x sin x
sin x cos x
№5 №3
4x
tgx 4
-3
5 -3x №4
Какая из двух функций
является первообразной
для другой?
Слайд 6
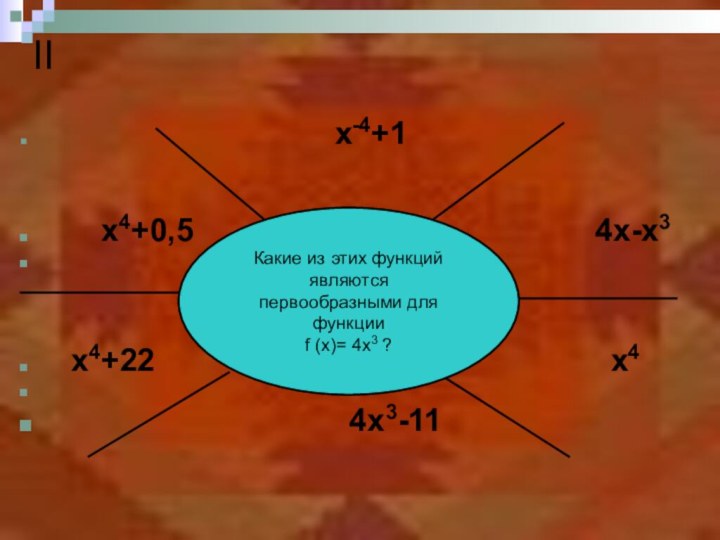
II
x-4+1
x4+0,5 4x-x3
x4+22 x4
4x3-11
Какие из этих функций являются
первообразными для функции
f (x)= 4x3 ?
Слайд 7
Мозаика фактов.
Термин «Первообразная» ввёл в 1797 году
французский ученый Луи Жозеф Лагранж (1736-1813). Ранее существовало другое
название.Какое?????
Решив примеры на вычисление интегралов, вы получите этот термин.
20 – п
3 – р
6 – и
1 – н 9 – м
-2 – а
Слайд 9
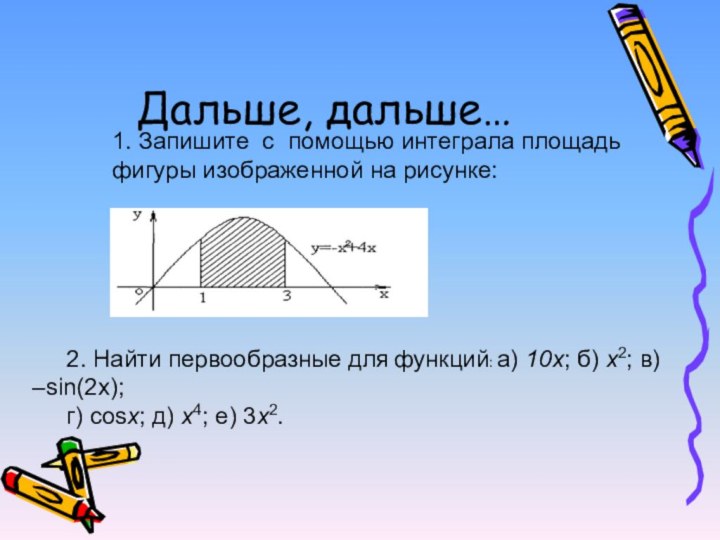
Дальше, дальше…
1. Запишите с помощью интеграла площадь фигуры
изображенной на рисунке:
2. Найти первообразные для функций: а) 10х;
б) х2; в) –sin(2x);г) cosx; д) х4; е) 3х2.
Слайд 11
1. Как называется функция F(x)?
2. Что является
графиком функции у=ах+b?
3. Самая низкая школьная оценка.
4. Какой урок
обычно проходит перед зачетом?5. Синоним слова дюжина?
6. Есть в каждом слове, у растения и может быть у уравнения.
7. Что можно вычислить при помощи интеграла?
8. Одно из важнейших понятий математики.
9. Форма урока, на котором проводится проверка знаний.
10.Немецкий ученый, в честь которого названа формула,
связывающая площадь криволинейной трапеции и интеграл.
11. плоскости с координатами (x, f(x)), где х пробегает область определения функции f.
12.Соответствие между Множество точек множествами Х и Y, при котором каждому значению множества Х поставлено в соответствие единственное значение из множества Y, носит название ....
Кроссворд
Слайд 12
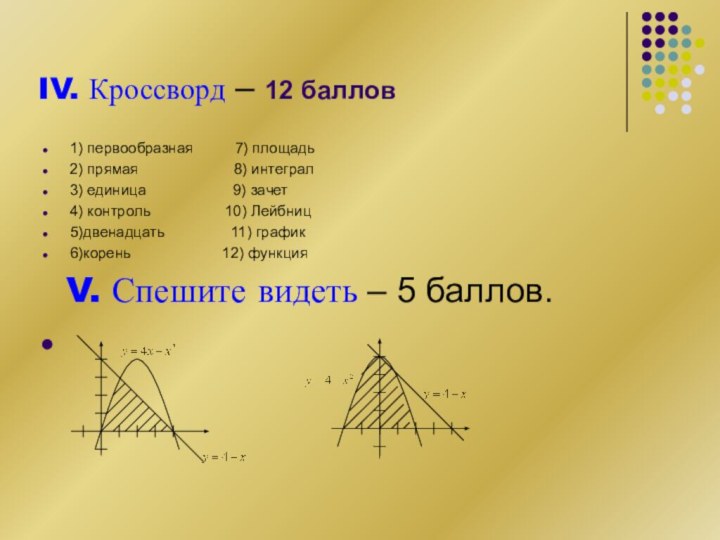
Изобразить криволинейную трапецию, ограниченную:
а) графиком функции у
=4х – х2, осью ОХ и прямой у=4 –
х;б) графиком функции у = 4 – х2, осью ОХ и прямой у=4 – х.
Спешите видеть!
Слайд 13
Задание 1.
Для функции f(х)=
Найти первообразную, график которой
проходит через
точку М(4;5).
А) F(х)= +3
Б) F(х)=2
+1 В) F(х)=2 +3
Г) F(х)= +5
Выполнить тест:
Слайд 14
Задание 2
С помощью формулы Ньютона-Лейбница вычисляют:
Б. Площадь криволинейной трапеции
В. Интеграл
Г. Производную
Слайд 15
Задание 3
Найти площадь фигуры, ограниченной осью ОХ и
параболой У=Х2
А. 36
Б.18
В.72
Г.Нельзя вычислить
Слайд 17
I. Разминка -8 баллов.
Задание 1
Задание 2
№1 -cosx х4 ; х4+22; х4+
№2 sinx
№3 4х
№4 5-3x
№5 tgx
II. Мозаика фактов – 11 баллов.
III. Дальше, дальше… - 11баллов.
1)
2) а) 5х2+С; б) в) ; г) sinx +С ; д) е)х3 +С
3) ИЛЛЛИЛ
ответы
Слайд 18
IV. Кроссворд – 12 баллов
1) первообразная
7) площадь
2) прямая
8) интеграл3) единица 9) зачет
4) контроль 10) Лейбниц
5)двенадцать 11) график
6)корень 12) функция
V. Спешите видеть – 5 баллов.





























