Презентация на тему по математики на тему Примеры комбинаторных задач (9 класс)

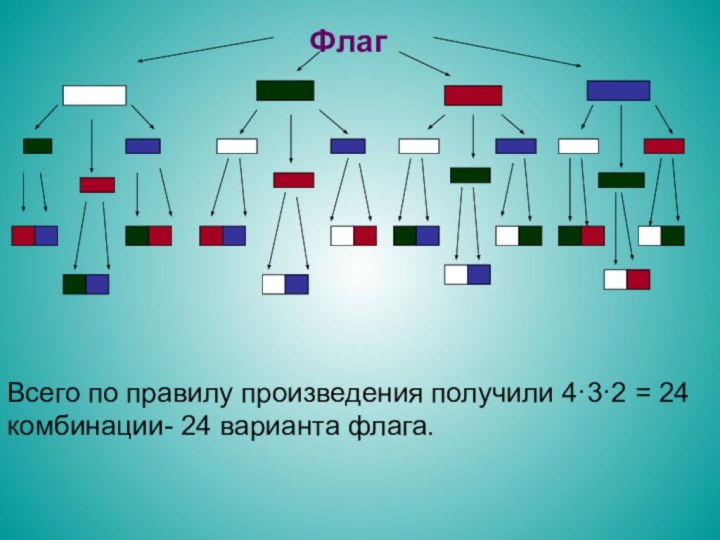
решению задач на перебор различных вариантов, удовлетворяющих каким-либо условиям.
В

комбинаторных задачах обычный вопрос: сколькими способами…Рождение комбинаторики как раздела математики связано с трудами великих французских математиков XVII века Блеза Паскаля и Пьера Ферма.

Существует очень много задач, в которых рассматриваются различные ситуации выбора. Однако, несмотря на все разнообразие комбинаторных задач, можно выделить среди них
группы однотипных. В этих задачах
речь идет о разных предметах, приводятся разные
ситуации, но ход их решения одинаков, и именно
поэтому такие задачи можно объединить в отдельные
группы.

из цифр 0, 1, 2, 4, 5, 9?
Решение.
Первые цифры

искомых чисел: 1, 2, 4, 5,9, так как в двузначном числе на первом месте может стоять любая цифра, кроме 0. Так как нужно составить четные двузначные числа, то второй цифрой искомых чисел могут быть: 0,2,4.
Составим таблицу: 5 строк (цифры 1,2,4,5,9) и 3 столбца(0,2,4) соответственно.

а вторая цифра- метке столбца. По строкам и столбцам

мы пересчитаем все возможные варианты, значит, искомых чисел будет столько же, сколько клеток в таблице, то есть 3 *5= 15.
Ответ: из цифр 0,1,2,4,5,9 можно составить 15 четных двузначных чисел.

В этой задаче мы осуществили полный перебор всех возможных вариантов ( комбинации). Поэтому подобные задачи называются комбинаторными.

ученик может выбрать булочку, ватрушку, кекс или сочник, а

запить их он может соком, чаем или компотом. Сколько вариантов завтрака предлагается в школьной столовой?

Решение: Собираем все варианты в таблицу.

образуют 12 клеток. Так как выбор еды и напитка

происходит независимо, то в каждой клетке будет стоять один из возможных вариантов завтрака. С другой стороны, любой вариант завтрака записан в одной из клеток. Значит, всего вариантов столько, сколько клеток в таблице, то есть 12.
Ответ: столовая предлагает 12 вариантов завтрака.

горизонтальных полос одинаковой ширины и различных цветов- белого, зеленого,

красного и синего? Есть ли среди этих флагов Государственный флаг Российской Федерации?

Решение: Рассмотрим составление всевозможных вариантов флага с помощью графа, названого деревом ( за внешнее сходство с деревом)

белый, синий, красный.

которое получило в комбинаторике название «Правило произведения»: если существует

n вариантов выбора первого элемента и для каждого из них есть m вариантов выбора второго элемента, то всего существует n · m различных пар с выбранным первым и вторым элементами.
Это правило справедливо для любого количества элементов.

комбинации- 24 варианта флага.

в записи которых все цифры различны?
Решение: На месте сотен

в числе, кратном пяти может стоять любое из 8: 1, 2,3, 4, 6,7,8,9, число не может начинаться с цифры нуль, и мы не можем использовать цифру 5.
На месте десятков может стоять любое из 7, так как не будет повторяться та цифра, которая стоит на месте сотен. На месте единиц может стоять только цифра 0 или 5, так как числа кратны пяти.
По правилу произведения получаем:
8·7·2 = 112

Ответ: 112 чисел.

с согласной буквы, а заканчивается гласной. Сколько открытых двухбуквенных

слогов можно написать, используя буквы «а», «б», «в», «г», «е», «и», «о»?

Решение: 4 (количество гласных) * 3 (количество согласных) = 12. Все слоги легко выписать, если заполнить таблицу.

Ответ: 12

Проказница Мартышка,
Осёл,
Козёл

Да косолапый Мишка
Затеяли сыграть Квартет.
……….. Ударили в смычки, дерут , а толку нет.
« Стой, братцы, стой! – кричит Мартышка.-
Погодите!
Как музыке идти? Ведь вы не так сидите»
Сколькими различными способами могут попытаться сесть эти музыканты?

Решение: 4* 3*2*1 = 24