Слайд 2
Цель:
Систематизируем и расширим знания по теме «Логарифмы»;
Рассмотрим
практическое и теоретическое применение логарифмов;
Решим логарифмы из заданий
ЕГЭ;
И просто отдохнем вместе с логарифмами.
Слайд 5
Группа «Математики-теоретики»
Логарифмы в математике
Цель: Определить
необходимость изучения логарифмов в математике
Задачи:
Сбор информации
Обработка информации
Формулировка чёткого ответа
на ключевой вопрос
Создание презентации
Представление своего исследования
Слайд 6
ОСНОВОПОЛАГАЮЩИЙ ВОПРОС:
Возможна ли математика без логарифмов?
Слайд 8
Слово «логарифм» происходит от греческих слов λσγοϕ -
число и αριυμοϕ - отношение. Переводится как «отношения чисел»,
одно из которых является членом арифметической прогрессии, а другое –геометрической.
Логарифм – толкование, значение
Словарь русского языка С. И. Ожегова
Логарифм - в математике: показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число.
Толковый словарь живого великорусского языка" В. Даль
Логарифм . Если под рядом чисел геометрической прогрессии (лествицы) выставить ряд отвечающих им чисел арифметической прогрессии, то каждое из последних будет логарифмом дружки своей, в первом порядке; сим способом умножение обращают в сложение, деление в вычитанье, что и облегчает выкладки.
Слайд 9
Свойства
логарифмов
«Осознав, что в математике нет ничего более скучного
и утомительного, чем умножение, деление, извлечение квадратных и кубических
корней, и что названные операции являются бесполезной тратой времени и неиссякаемым источником неуловимых ошибок, я решил найти простое и надежное средство, чтобы избавиться от них».
Джон Непер, «Канон о логарифмах»
Слайд 10
«Логарифмы бывают разные…»
Бригсов логарифм - то же, что
десятичный логарифм.
Назван по имени Г. Бригса
Десятичный логарифм -
логарифм по основанию 10. Десятичный логарифм числа а обозначают lgа
Натуральный логарифм - логарифм, основание которого - неперово число е = 2,718 28... Натуральный логарифм числа а обозначают ln а.
Неперов логарифм - (по имени Дж. Непера), то же, что натуральный логарифм
Джон Непер (1550-1617)
Генри Бригс (1561-1631)
Слайд 11
«Золотые» логарифмы
В мире нет ничего, кроме Красоты.
В Красоте
нет ничего, кроме Формы.
В Форме нет ничего, кроме пропорций.
В
пропорциях нет ничего, кроме Числа.
Пифагор
Три основания логарифмов:
10,000; 3,838; 2,71.
«Золотые» логарифмы – это логарифмы с основанием равным числу
Ф (1, 6180339) описываются формулой
logФ M = P
Слайд 12
Простые и сложные проценты
Через сколько лет банковский вклад
в 10 тыс. рублей при процентной ставке 10 %
годовых вырастет в миллион?
Сложные процентные
ставки вычисляются по формуле:
Где n – срок увеличения вклада,
S – первоначальная сумма вклада,
Sn – итоговая сумма вклада,
P – процентная ставка
Простые процентные ставки вычисляются так:
Слайд 13
Зачем мы изучаем логарифмы?
Во-первых, логарифмы и сегодня позволяют
упрощать вычисления.
Во-вторых, испокон веков целью математической науки было
помочь людям узнать больше об окружающем мире, познать его закономерности и тайны.
Логарифмы – важные составляющие не только математики, но и всего окружающего мира, поэтому интерес к ним не ослабевает с годами и их необходимо продолжать изучать.
Слайд 14
Группа «Историки»
История появления логарифмов
Цель:
Задачи:
Проект предполагает сбор и анализ
данных, их представление в четком визуальном виде и направлен
на формирование понимания содержательного смысла термина «логарифм»
Установить картину возникновения понятия «логарифм»
Слайд 15
Кем и когда
были введены логарифмы?
Слайд 16
Изобретение логарифмов тесно связано с развитием в XVI
в. производства и торговли, астрономии и мореплавания. Требовались новые
методы вычислений.
Слайд 17
Открытие логарифма
Архиме́д ( III в. до н.э.) —
древнегреческий физик, механик и инженер из Сиракуз.
Изобретение логарифмов, сократив
работу астронома, продлило ему жизнь.
П. С. Лаплас
Продолжил работу в XVI веке шотландский барон Непер
Слайд 18
История развития логарифмов
Я всегда старался, насколько позволяли
мои силы и способности, освободить людей от трудности и
скуки вычислений, докучливость которых обыкновенно отпугивает очень многих от изучения математики
Палочки Непера
Джон Непер
1550—1617 г
Слайд 19
Непер Джон (1550—1617) — шотландский математик, изобретатель логарифмов.
Учился в Эдинбургском университете. Основными идеями учения о логарифмах
Непер овладел не позднее 1594, однако его «Описание удивительной таблицы логарифмов», в котором изложено это учение, было издано в 1614.
В этом труде содержались определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.
Слайд 20
Непер вошёл в историю как изобретатель замечательного вычислительного
инструмента — таблицы логарифмов. Это открытие вызвало гигантское облегчение
труда вычислителя.
В честь Джона Непера названы:
кратер на Луне;
астероид 7096 Непер;
логарифмическая безразмерная единица, измеряющая отношение двух величин;
университет в Эдинбурге
Слайд 21
Непер изобрёл счётный прибор - «палочки Непера». позволявшие
производить операции умножения и деления непосредственно над исходными числами.
В основу данного метода Непер положил способ умножения решеткой.
Слайд 22
Логарифмическая линейка - инструмент вычислений
В 1623 г. английский
математик Д. Гунтер изобрёл первую логарифмическую линейку, ставшую рабочим
инструментом для многих поколений.
Принцип действия логарифмической линейки основан на том, что умножение и деление чисел заменяется соответственно сложением и вычитанием их логарифмов.
Слайд 23
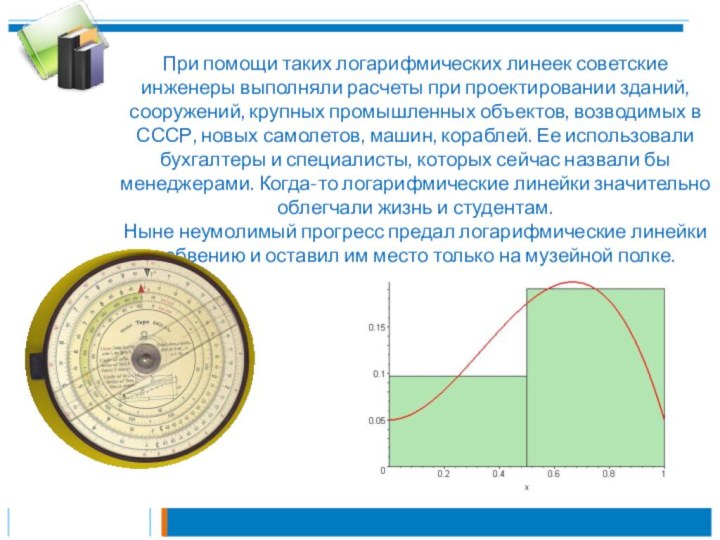
Логарифмические линейки были двух видов. Первые выглядели такими,
как и представленная на снимке. Они отличались длиной (от
15 до 50-75 см.), от нее зависела точность вычислений. Вторые напоминали часы: несколько шкал по окружности подвижного циферблата, стрелочки, неподвижная метка. Однако принцип в них был заложен одинаковый.
Слайд 24
Цилиндрическая логарифмическая линейка
Инженерно –навигационная
логарифмическая линейка
Круговая логарифмическая
линейка
Логарифмическая
линейка
Слайд 25
При помощи таких логарифмических линеек советские инженеры выполняли
расчеты при проектировании зданий, сооружений, крупных промышленных объектов, возводимых
в СССР, новых самолетов, машин, кораблей. Ее использовали бухгалтеры и специалисты, которых сейчас назвали бы менеджерами. Когда-то логарифмические линейки значительно облегчали жизнь и студентам.
Ныне неумолимый прогресс предал логарифмические линейки забвению и оставил им место только на музейной полке.
Слайд 26
Логарифмы — это все! Музыка и звуки!
И без
них никак нельзя обойтись науке!
Вот вы когда-нибудь слыхали
О
логарифмической спирали?
Слайд 27
Знаменитости и спираль
Впервые о логарифмической спирали говорится в
письме французского математика Рене Декарта в 1638 г.
Великий немецкий
поэт Иоганн Вольфганг Гете считал логарифмическую спираль математическим символом жизни.
Логарифмическая спираль так поразила математика Якоба Бернулли, что он завещал высечь ее изображение на своем надгробном камне вместе с надписью на латинском «Измененная, возрождаюсь прежней».
Слайд 28
ЛОГАРИФМИЧЕСКАЯ «КОМЕДИЯ 2 > 3»
Комедия начинается с неравенства
бесспорно правильного.
Затем
следует преобразование тоже не внушающее сомнение.
Большему числу соответствует больший логарифм, значит,
После сокращения на lg получаем: 2>3.
В чем ошибка этого рассуждения?
Ошибка в том, что lg <0, поэтому после сокращения на него знак неравенства надо было поменять.
Слайд 29
ВЫВОД:
Мы постарались проследить, как в ходе истории возникала
необходимость введения и изучения логарифмов, усиливалась их значимость.
Слайд 30
Группа «Науковеды»
Цель:
Задачи:
Логарифмы - это обычные математические понятия или
нечто большее?!
В каких науках применяются логарифмы
Как многие
реальные объекты астрономии, биологии, физики, химии и других естественных наук связаны с логарифмами?
Слайд 31
Зачем логарифмы в современном мире? Интересное и удивительное
о логарифмах!
С появлением персональных компьютеров роль логарифмов значительно уменьшилась?
Слайд 32
Логарифмы в физике и астрономии
Слайд 33
Область применения логарифмов весьма разнообразна: математика, литература, биология,
психология, сельское хозяйство, музыка, астрономия, физика
«Изобретение логарифмов, сократив
работу астронома, продлило ему жизнь».
Мы бы ничего не знали о звездах, если бы не логарифмы!
Логарифмы в физике и астрономии
Звёзды
Во II веке до н.э. Гиппарх разделил звезды на 6 групп. Самые яркие – звезды 1-ой величины, самые слабые – 6-ой величины.
Установлено, что звезда 1-ой вел. ярче звезды 6-ой вел. ровно в 6 раз.
звезда 1 вел. ярче зв. 2 вел. в 2,512;
звезда 1 вел. ярче зв. 3 вел. В 2,5122;
«Величина» звезды есть не что иное, как логарифм ее физической яркости.
Так что астрологи, оценивая видимую яркость звезд, оперируют с таблицей логарифмов, составленный
при основании 2,512.
Слайд 34
Логарифмы и логарифмическая спираль в химии
Водородный показатель pH —
это мера активности ионов водорода в растворе, количественно выражающая
его кислотность, вычисляется как отрицательный десятичный логарифм концентрации водородных ионов, выраженной в молях на литр:
pH = -lg [H+]
Геометрическая форма таблицы Менделеева
Слайд 35
Логарифмы и мы
Человеческий организм воспринимает и «логарифмирует» ощущения:
Мера
непрозрачности роговицы глаза
Уровень звукового восприятия
Электрическая активность нейронов головного
мозга
Слайд 36
Логарифмическая спираль в биологии
Слайд 37
Логарифмическая спираль в технике
И эту спираль мы повсюду
встречаем:
К примеру, ножи в механизме вращая.
В изгибе трубы мы
ее обнаружим —
Турбины тогда максимально послужат!
Слайд 38
Логарифмическая спираль в архитектуре
Слайд 40
Номера клавишей рояля представляют собой логарифмы чисел колебаний
соответствующих звуков.
Величина ощущения пропорциональна логарифму величины раздражения
Слайд 41
Один из наиболее распространенных пауков ЭПЕЙРА, сплетая паутину,
закручивает нити вокруг центра по логарифмической спирали
По логарифмическим
спиралям закручены и многие галактики, в частности, галактика, которой принадлежит Солнечная Система
Спиральная галактика Водоворот
Слайд 42
В литературе
Любопытная задача, взятая из книги “Господа Головлевы”
Салтыкова-Щедрина:
“Порфирий Владимирович сидит у себя в кабинете, исписывая цифирными
выкладками листы бумаги. На этот раз его занимает вопрос: Сколько было бы у него денег, если бы маменька подаренные ему при рождении дедушкой на зубок 100 рублей не присвоила себе, а положила в ломбард на имя малолетнего Порфирия? Выходит, однако, немного: всего 800 рублей?
Предполагая, что Порфирию в момент расчета было 50 лет, и, сделав допущение, что он произвел вычисления правильно (допущения маловероятное, т.к. едва ли Головлев знал логарифмы и умел вычислять сложные проценты), требуется установить, сколько % платил в то время ломбард.
Слайд 44
Однако в начале XXI века логарифмические линейки получили
второе рождение в наручных часах. Дело в том, что
следуя моде производители дорогих и престижных марок часов перешли от электронных хронометров с ЖК- экранами к стрелочным и соответственно места для встраиваемого калькулятора оказалось недостаточно. Однако спрос на хронометры со встроенным вычислительным устройством среди следящих за модой людей заставил производителей часов выпустить модели с встроенной логарифмической линейкой выполненной в виде вращающихся колец со шкалами вокруг циферблата.
Слайд 45
Заключение
Поистине безграничны приложения логарифмической функции и логарифмов в
самых различных областях науки и техники.
Многообразное применение функции
вдохновило английского поэта Э. Брилла на написание оды о логарифмах.
Были поэты, которые не посвящали логарифмам целых од, но упоминали их в своих стихах. Известный поэт Борис Слуцкий в своём нашумевшем стихотворении «Физики и лирики» писал:
«Потому-то, словно пена,
Опадают наши рифмы
И величие степенно
Отступает в логарифмы».
Выполняя данную работу, мы сделали для себя открытие, что логарифмы и логарифмическая функция помогли человеку следовать путём технического прогресса и объяснить многие тайны природы, человеческих ощущений. Быть может человечество стоит на пороге новых революционных открытий, и поможет нам в этом «царица наук»- математика!
Слайд 46
Мы рассказали вам о логарифмах,
и показали их
в картинках!
Надеемся, вы поняли, для чего они нужны
и как
в поэзии важны!
И может быть когда-то своим детям расскажете о логарифме этом!
Слайд 47
ПОДГОТОВКА К ЕГЭ
Группа «Математики-практики»
Цель нашей
работы:
показать решение примеров, взятых из заданий ЕГЭ.
Мы поставили
перед собой задачу:
показать, что знания о логарифмах необходимы и на ЕГЭ по математике.
Слайд 48
Только зная все свойства логарифма, можно научиться решать
примеры
=
=
1
=
=
b
r
a
log
Слайд 52
Вывод:
логарифмы – важные составляющие не только математики,
но и всего окружающего мира, поэтому интерес к ним
не ослабевает с годами и их необходимо продолжать изучать.
Конкурс №1
Назовите фамилию математика, который продолжил работу Непера по созданию таблиц логарифмов?
Ключ к ответу:
Ответ: Бригс
Мини – соревнования
Слайд 54
Конкурс №2
Укажите географические координаты острова Ян - Майен,
где проживал Непер – создатель логарифмов.
Географические координаты:
х°00′
северной широты,
у°00′ западной долготы.
Чтобы найти х и у, решите уравнения:
Ответ:
71°00′ северной широты,
8°00′ западной долготы
Слайд 55
Здесь лежит результат деятельности многих ученых . То,
что здесь находится использовалось в учебных заведениях и инженерных
расчетах до конца прошлого века.
Черный ящик
Слайд 56
Здесь лежит, то что еще в 20 годах
17 века придумал английский математик Уильям Отред.
«Считать на ней
можно быстро, места почти не занимает, её можно всюду носить с собой в кармане»
а с т н
о о
с у м е
о с н в а н и е
п о к з а т е л ь
н е п е
д е с я т ч н ы й
л о г а р и м и р о в а н и е
Кроссворд
Слайд 59
Любимая цифра
А теперь возьмите, пожалуйста, ручки и запишите
свою любимую цифру.
Умножьте эту цифру на 9. Полученное число
умножьте на 12345679.
Если Вы сделали правильно, то у Вас получится букет из Ваших любимых цифр. А теперь припишите справа к полученному числу 9 нулей. Пусть в Вашей жизни будет столько счастливых дней.