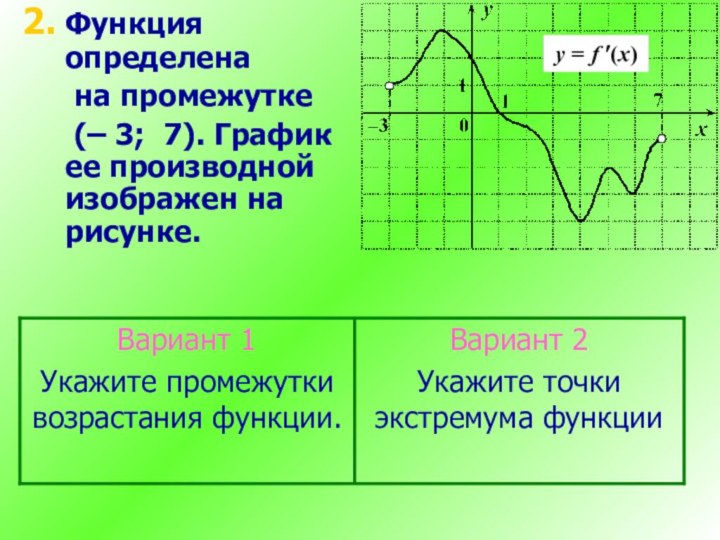
(– 6; 4). График ее производной изображен на рисунке.
Укажите точку
максимума функции у = f(x) на этом промежутке.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


![Презентация Примеры применения производной (алгебра и начала анализа. 10 класс) Функция у = f(x) задана на промежутке [–6; 4]. Укажите промежуток, которому принадлежат все точки экстремума.](/img/tmb/7/645888/8f65e14c47c596d409d9e647e664b42c-720x.jpg)
![Презентация Примеры применения производной (алгебра и начала анализа. 10 класс) Функция у = f (x) задана на отрезке [a; b]. На рисунке](/img/tmb/7/645888/f0552913d72815d12551daed8924d7cf-720x.jpg)












В 19 лет он стал профессором в Артиллерийской школе Турина. Именно Лагранж в 1791 г. ввёл термин «производная», ему же мы обязаны и современным обозначением производной (с помощью штриха). Термин «вторая производная» и обозначение(два штриха) также ввёл Лангранж
Задача определения скорости прямолинейного неравномерного движения была впервые решена Ньютоном. Функцию он назвал флюэнтой, т.е. текущей величиной, производную же – флюксией. Ньютон пришел к понятию производной, исходя из вопросов механики. Предполагают, что Ньютон открыл свой метод флюксий ещё в середине 60-х годов XVII в.
Первый общий способ построения касательной к алгебраической кривой был изложен в «Геометрии» Декарта. Более общим и важным для развития дифференциального исчисления был метод построения касательных Ферма.