- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Электронный образовательный ресурс по теме Повторим функцию
Содержание
- 2. Знание законов
- 3. Линейная функция у = кх + вСвойства
- 4. Линейная функцияПри к > 0 график расположен в I и III четвертив0
- 5. Линейная функцияПри к > 0 график расположен во II и IV четвертив0
- 6. Функция у = к/х и ее график.1.
- 7. Функция у = к/х и ее график.
- 8. Функция у = x2Свойства функции:1. Если х
- 9. Квадратичная функцияСвойства квадратичной функции1) Область определения: R2)
- 10. 5) Промежутки знакопостоянства
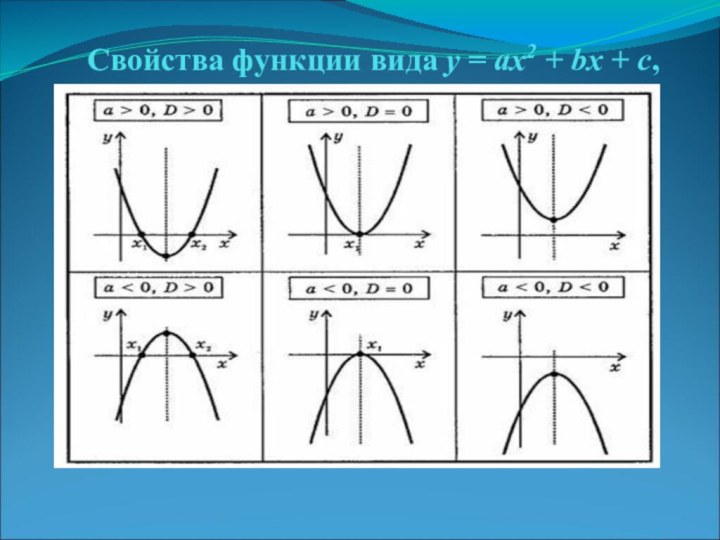
- 11. Свойства функции вида y = ax2 + bx + c,
- 12. Кубическая функция y=x³1.Область определения – любое действительное
- 13. Свойства функции1) D(у) = [0;∞).2)E(у) = [0;∞).3)
- 14. Функция у = |x|Свойства функции y=|х|1. D(у)
- 15. Скачать презентацию
- 16. Похожие презентации
Знание законов природы дало человеку возможность объяснять и предсказывать её разнообразнейшие явления. «Математическими портретами» закономерностей природы и служат функции.










Слайд 3
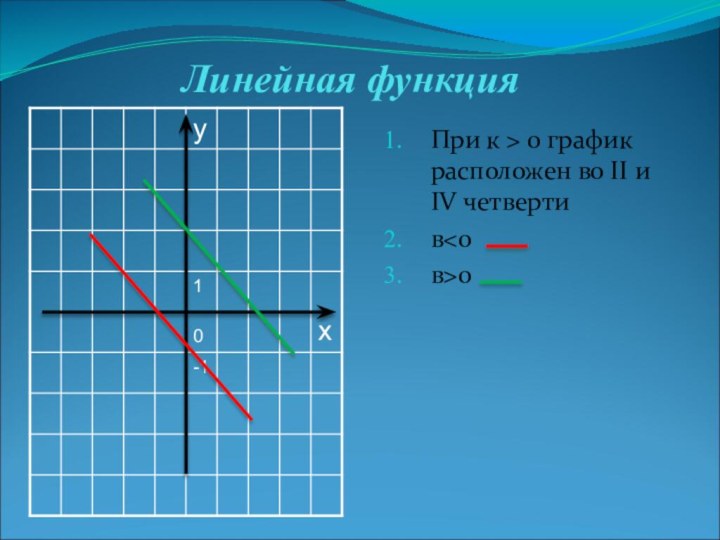
Линейная функция у = кх + в
Свойства функции
1.Х
Є R
2.У Є R
3. Прямая
4. с ОХ:
Х = -в / к5. с ОУ: у = в
6. если к = 0, то график | | оси ОХ или совпадает с ней.
у=кх
у=кх+в
Слайд 6
Функция у = к/х и ее график.
1.
2.
3. у > 0, если х
у
0, если х ϵ ;4. функция убывает при х U
5. нечётная, симметрична начала координат.
.
Слайд 7
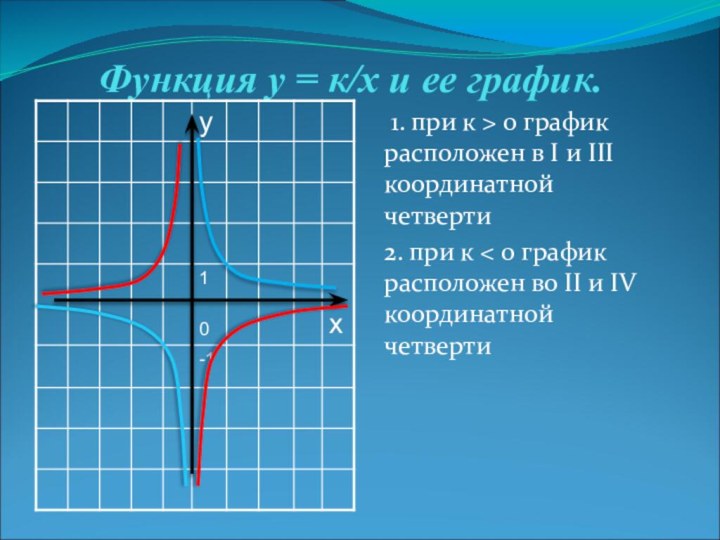
Функция у = к/х и ее график.
1.
при к > 0 график расположен в I и
III координатной четверти2. при к < 0 график расположен во II и IV координатной четверти
Слайд 8
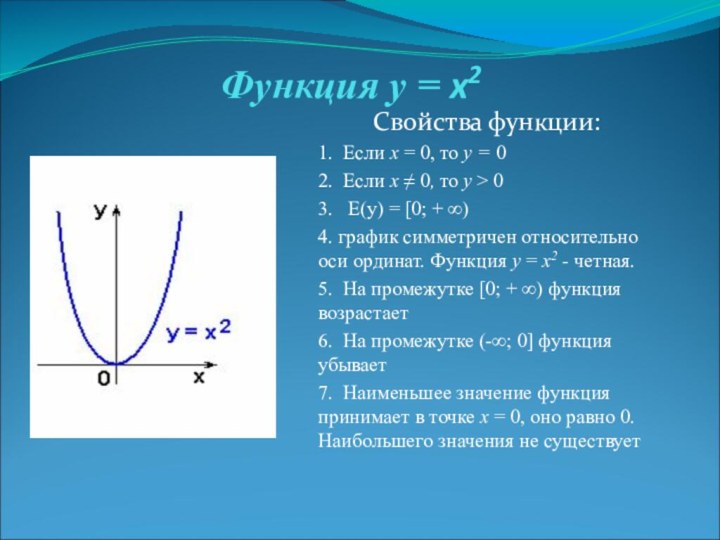
Функция у = x2
Свойства функции:
1. Если х =
0, то у = 0
2. Если х ≠ 0,
то у > 03. Е(у) = [0; + ∞)
4. график симметричен относительно оси ординат. Функция у = х2 - четная.
5. На промежутке [0; + ∞) функция возрастает
6. На промежутке (-∞; 0] функция убывает
7. Наименьшее значение функция принимает в точке х = 0, оно равно 0. Наибольшего значения не существует
Слайд 9
Квадратичная функция
Свойства квадратичной функции
1) Область определения: R
2) Область
значений при а > 0 [-D/(4a); ∞)
при
а < 0 (-∞; -D/(4a)]3) Четность, нечетность
при b = 0 функция четная
при b ≠ 0 функция не является ни четной, ни нечетной
4) Нули функции
при D > 0 два нуля: ,
при D = 0 один нуль функции:
при D < 0 нулей функции нет
Слайд 10 5) Промежутки знакопостоянства если, а > 0, D
> 0, то если, а > 0, D =
0, то eсли а > 0, D < 0, то если а < 0, D > 0, то если а < 0, D = 0, то если а < 0, D < 0, то 6) Промежутки монотонности при а > 0 при а < 0
Слайд 12
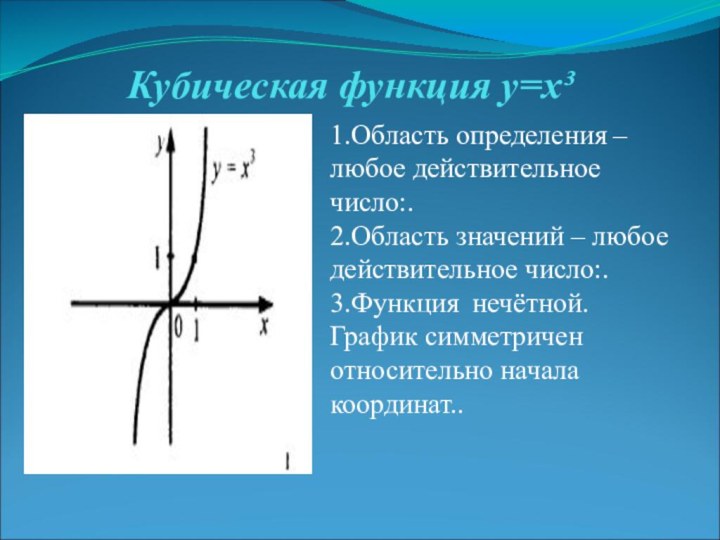
Кубическая функция y=x³
1.Область определения – любое действительное число:.
2.Область
значений – любое действительное число:. 3.Функция нечётной. График симметричен относительно
начала координат..
Слайд 13
Свойства функции
1) D(у) = [0;∞).
2)E(у) = [0;∞).
3) Функция
имеет один нуль:
y=0 при x=0.
4) Функция возрастает на всей
[0;∞). 5). унаим = 0, унаиб не существует
функция непрерывная
Слайд 14
Функция у = |x|
Свойства функции y=|х|
1. D(у) =
(-∞; ∞).
2). E(y) = [0; ∞).
3). y=0 при x=0.
4).
График симметричен относительно оси 5). |-х|=|х|, то есть y=|х| — чётная функция.6) Функция убывает при x∈(-∞; 0) и возрастает при x∈(0; ∞).
у = - |x|
у = |x|





























