работать с числами с рациональным показателем степени.
На этом
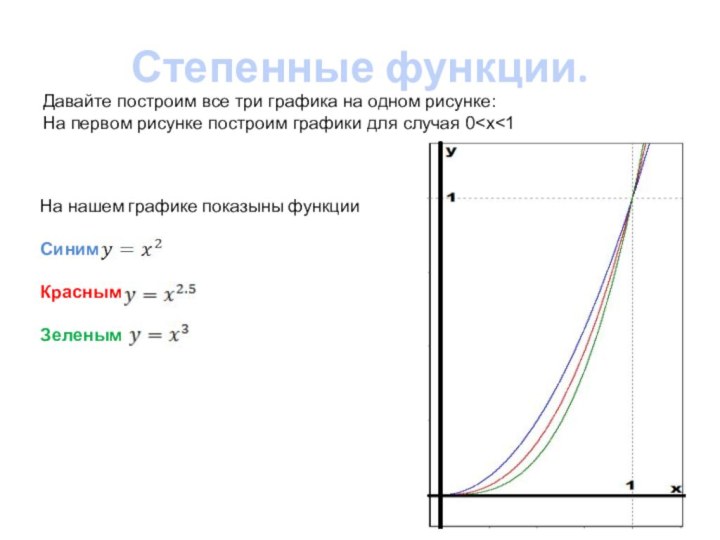
уроке мы рассмотрим степенные функции и ограничимся случаем, когда показатель степени рациональный.Мы будем рассматривать функции вида:
Рассмотрим сначала функции, у которых показатель степени больше одного.


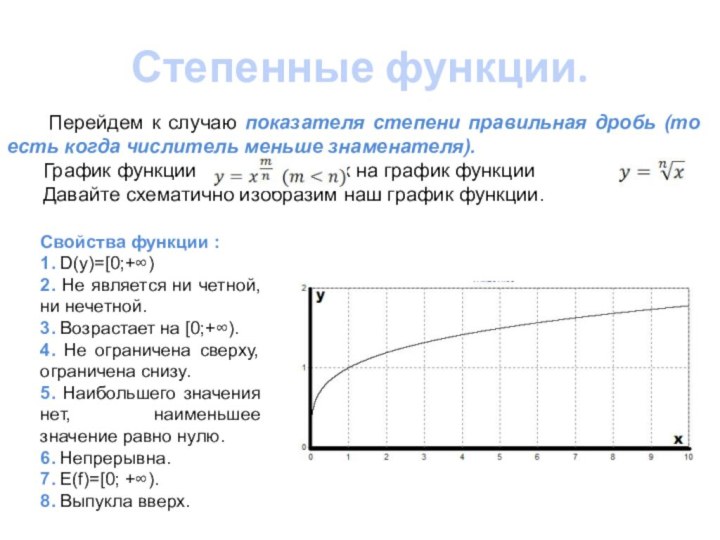
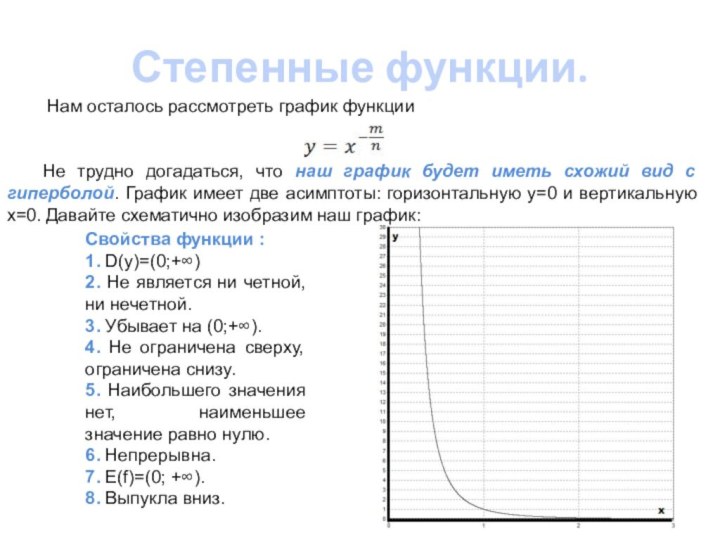

![Презентация к уроку алгебры 11 класс по теме Степенные функции Степенные функции. Пример. Найти наибольшее и наименьшее значение функции на отрезке: а) [1;16] б) (2,10) в)](/img/tmb/7/653829/1cd582c485a83d6f578b29403c530d20-720x.jpg)
![Презентация к уроку алгебры 11 класс по теме Степенные функции Степенные функции. Пример. Найти наибольшее и наименьшее значение функции на отрезке [1;9]. Решение. Ребята, вы](/img/tmb/7/653829/70e7d562bc40c5e2c19af39e291615c1-720x.jpg)

































