- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему (к конспекту урока). Алгебра 7 класс. Формулы сокращенного умножения
Содержание
- 2. Цель: Повторение, обобщение, систематизация учебного материала
- 3. Задачи: Обучающие: -
- 4. Основные результаты Изучили понятия:Многочлен, двучлен, трехчленПриведение подобных
- 5. Основные результаты Формулы: Формулы сокращенного умноженияформулы разложения многочлена на множителиКвадрат суммыКвадрат разностиРазность квадратовРазность кубовСумма кубов
- 6. КРОССВОРД По теме: «Многочлены. Арифметические операции над
- 7. Ответы на кроссвордАлгебраическое выражение, которое представляет собой
- 8. Пары равных выражений
- 9. Практическая частьПрименение формул в комплексе в заданиях.Найти
- 10. Ответы к тексту Вариант №1Вариант №2КРИТЕРИИ ОЦЕНКИОценка
- 11. Домашнее заданиеРабота над ошибками текстаДомашняя контрольная работа
- 12. Контрольная работа Вариант А В СВариант
- 13. ВЫВОД:Знание формул сокращенного умножения и их своевременное
- 14. Скачать презентацию
- 15. Похожие презентации
Цель: Повторение, обобщение, систематизация учебного материала












Слайд 3
Задачи:
Обучающие:
- проверить
практические навыки и умения применять формулы как «слева направо»,
так и « справа налево».совершенствование навыков работы с тестами
обучение навыкам самопроверки и взаимопроверки
Развивающие:
- развитие навыков оперирования формулами
- развитие логического и математического мышление.
- развитие навыков сравнения, анализа
- развитие математической речи
- развитие активности, инициативы, интереса к предмету
Воспитывающие:
- воспитывать чувство уважения друг к другу, коллективизма
серьёзное и ответственное отношение к работе на уроке
Слайд 4
Основные результаты
Изучили понятия:
Многочлен, двучлен, трехчлен
Приведение подобных членов
многочлена
Взаимное уничтожение членов многочлена
Стандартный вид многочлена
Алгебраическая сумма многочленов
Изучили правила:
Правило
составления алгебраической суммы многочленовПравило умножения многочлена на одночлен
Правило умножения многочлена на многочлен
Правило деления многочлена на одночлен
Изучили формулы:
Формулы сокращенного умножения
формулы разложения многочлена на множители
Слайд 5
Основные результаты
Формулы:
Формулы сокращенного умножения
формулы разложения многочлена
на множители
Квадрат суммы
Квадрат разности
Разность квадратов
Разность кубов
Сумма кубов
Слайд 6
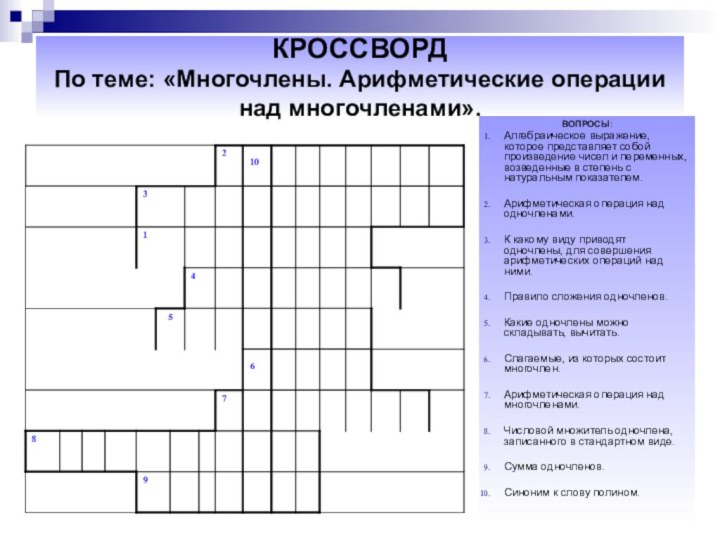
КРОССВОРД
По теме: «Многочлены. Арифметические операции над многочленами».
ВОПРОСЫ:
Алгебраическое выражение,
которое представляет собой произведение чисел и переменных, возведенные в
степень с натуральным показателем.Арифметическая операция над одночленами.
К какому виду приводят одночлены, для совершения арифметических операций над ними.
Правило сложения одночленов.
Какие одночлены можно складывать, вычитать.
Слагаемые, из которых состоит многочлен.
Арифметическая операция над многочленами.
Числовой множитель одночлена, записанного в стандартном виде.
Сумма одночленов.
Синоним к слову полином.
Слайд 7
Ответы на кроссворд
Алгебраическое выражение, которое представляет собой произведение
чисел и переменных, возведенные в степень с натуральным показателем.
(одночлен).Арифметическая операция над одночленами. (умножение).
К какому виду приводят одночлены, для совершения арифметических операций над ними. (стандартный).
Правило сложения одночленов. (алгоритм).
Какие одночлены можно складывать, вычитать. (подобные).
Слагаемые, из которых состоит многочлен. (члены).
Арифметическая операция над многочленами. (сложение).
Числовой множитель одночлена, записанный в стандартном виде. (коэффициент).
Сумма одночленов. (полином).
Синоним к слову полином (многочлен).
Слайд 9
Практическая часть
Применение формул в комплексе в заданиях.
Найти значение
выражения.
Представить в виде многочлена стандартного вида.
Решить уравнение.
Применение формул.
Геометрическая иллюстрация
формулы квадрата суммы.Показать как полученная формула используется для математических формул.
Тест по теме: «Формулы сокращенного умножения»
Слайд 10
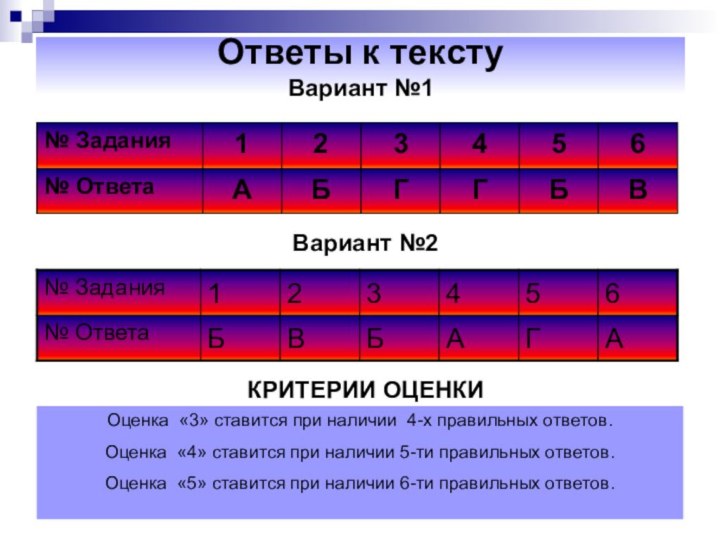
Ответы к тексту
Вариант №1
Вариант №2
КРИТЕРИИ ОЦЕНКИ
Оценка «3» ставится
при наличии 4-х правильных ответов.
Оценка «4» ставится при наличии
5-ти правильных ответов.Оценка «5» ставится при наличии 6-ти правильных ответов.
Слайд 11
Домашнее задание
Работа над ошибками текста
Домашняя контрольная работа
Предлагается дифференцированный подход знаний, задания распределены по трём
уровням сложности А, Б, С.А – обязательный
В - повышенный
С - высокий
КОНТРОЛЬНАЯ РАБОТА 3 - ВАРИАНТА
Слайд 12
Контрольная работа
Вариант А В С
Вариант А
1.Выполните действия.
2.Упростите
выражение.
3.Представить в виде произведения.
4.Решите уравнение.
Вариант В
1.Выполните действия
2.Упростите вы
ражение.
3.Представить в
виде произведения.4.Решите уравнение.
Вариант С
1.Выполните действия.
2Упростите выражение.
3.Представить в виде произведения.
4.Решите уравнение.
Слайд 13
ВЫВОД:
Знание формул сокращенного умножения и их своевременное применение
помогает сэкономить время, увидеть красоту в технике преобразования выражений.
Умелое
оперирование формулами используется в геометрии, физике и даже в цирковом жанре – математические фокусы. Формулы сокращенного умножения, как таблица, умножения будут использоваться на протяжении всего курса изучения алгебры, как одного из инструментов в преобразовании алгебраических выражений.