Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по математике Исследование графиков тригонометрических функций

Содержание

«Счастливая случайность выпадает лишь на долю подготовленных умов» Луи Пастер. .
Исследование и построение графиков тригонометрических функций (16.10.15)Алексеева Н.А. школа-гимназия №29 г.Бишкек «Счастливая случайность выпадает лишь на долю подготовленных умов» Луи Пастер. . Домашнее заданиеЗавести тетрадиВыучить схему исследования функцииРешить : №№ 100, 101, 102 - (г) тригонометрические функцииГрафиком функции у = sin x является синусоидаСвойства функции:D(y) =RПериодическая (Т=2π)Нечетная тригонометрические функцииГрафиком функции у = cos x является косинусоидаПеречислите свойства функции у тригонометрические функцииВ конспект:y =sin (x+ π/4)Постройте график функции:y =sin (x+ π/4) 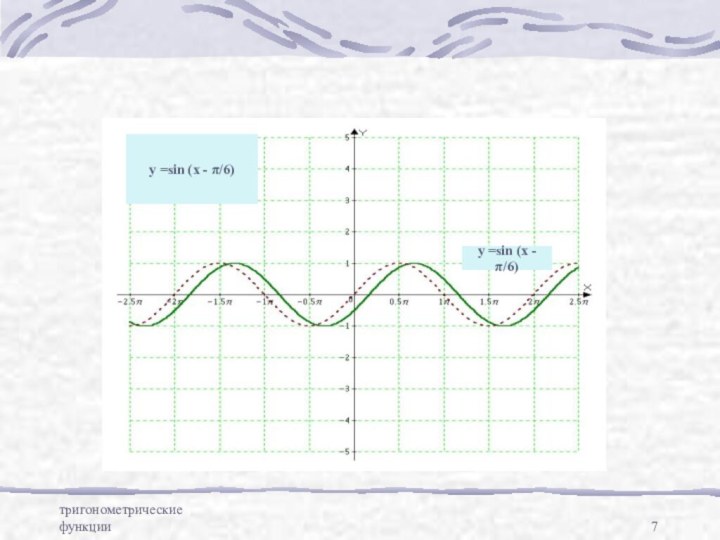тригонометрические функцииy =sin (x - π/6)y =sin (x - π/6) 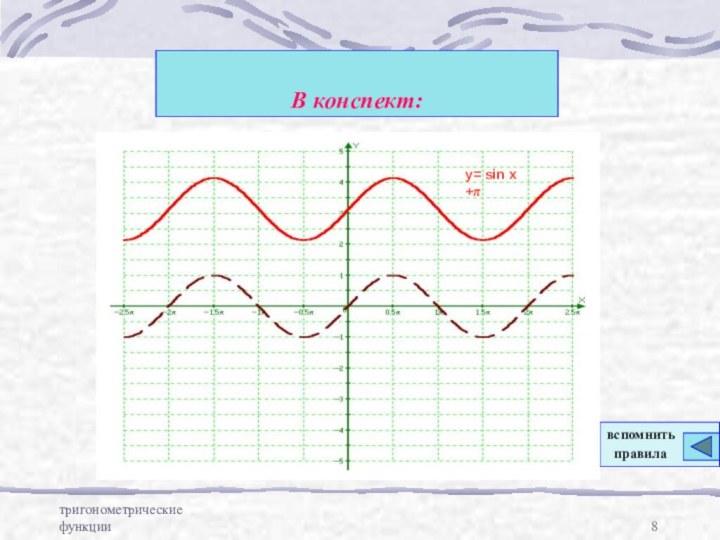тригонометрические функцииВ конспект:y= sin x +πвспомнить правила тригонометрические функцииВ конспект:График функции у = f (x+в) получается из графика функции 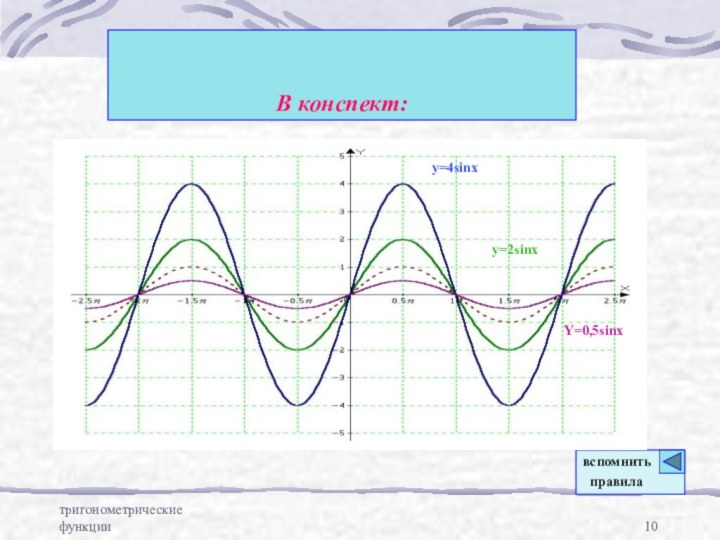тригонометрические функцииВ конспект:y=2sinxy=4sinxY=0,5sinxвспомнить правила тригонометрические функцииВ конспект:График функции у =k f (x) получается из графика функции 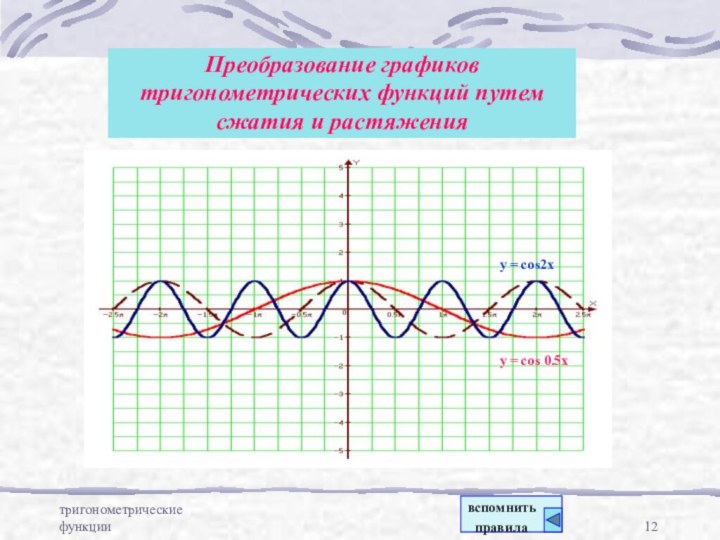тригонометрические функцииПреобразование графиков тригонометрических функций путем сжатия и растяженияy = cos2xy = cos 0.5xвспомнить правила тригонометрические функцииВ конспект:График функции у = f (kx) получается из графика функции 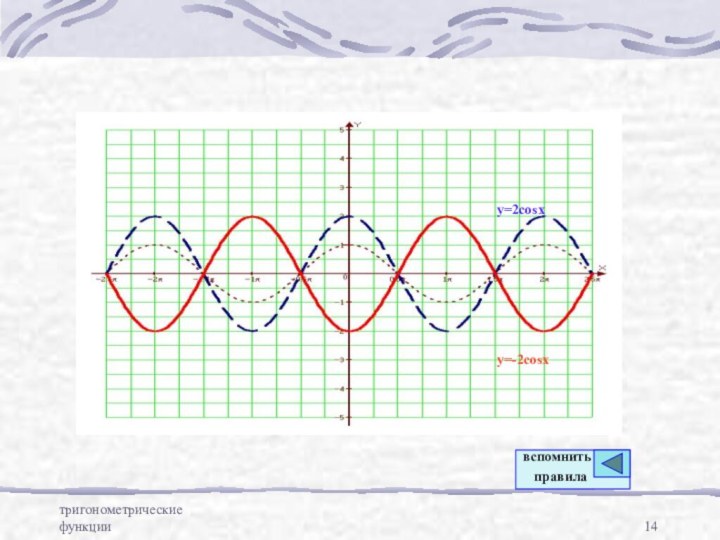тригонометрические функцииy=2cosxy=-2cosxвспомнить правила 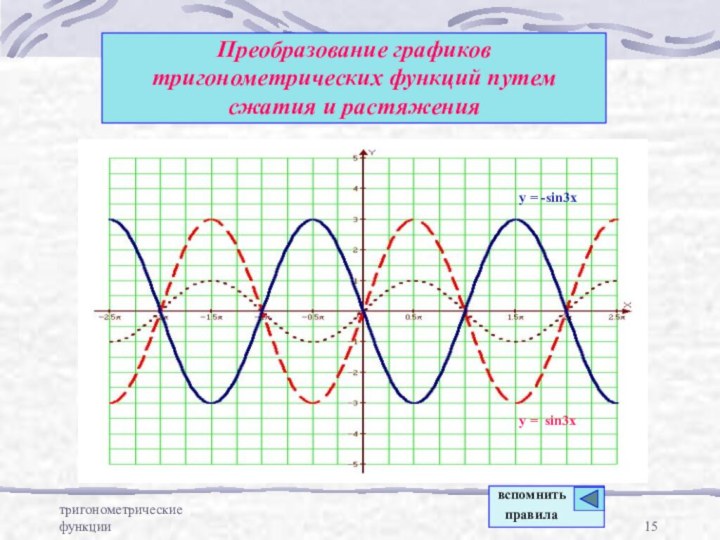тригонометрические функцииПреобразование графиков тригонометрических функций путем сжатия и растяженияy = -sin3xy = sin3xвспомнить правила тригонометрические функцииВ конспект:Графики функций у = -f (kx) и у=-k f(x) получаются ПРАКТИКУМ ( в конспект):№ № 100(а), 101(а), 102(а), 103(а) тригонометрические функцииПреобразование графиков тригонометрических функций путем сжатия и растяженияY= cos(2x+π/3)y=cos(x+π/6)y= cos(2x+π/3)y= cos(2(x+π/6))y=
Слайды презентации

Слайд 2 «Счастливая случайность выпадает лишь на долю подготовленных умов» Луи

«Счастливая случайность выпадает лишь на долю подготовленных умов» Луи Пастер. .

Пастер. .

Слайд 3
Домашнее задание
Завести тетради
Выучить схему исследования
функции
Решить : №№

Домашнее заданиеЗавести тетрадиВыучить схему исследования функцииРешить : №№ 100, 101, 102 - (г)

100, 101, 102 - (г)


Слайд 4 тригонометрические функции
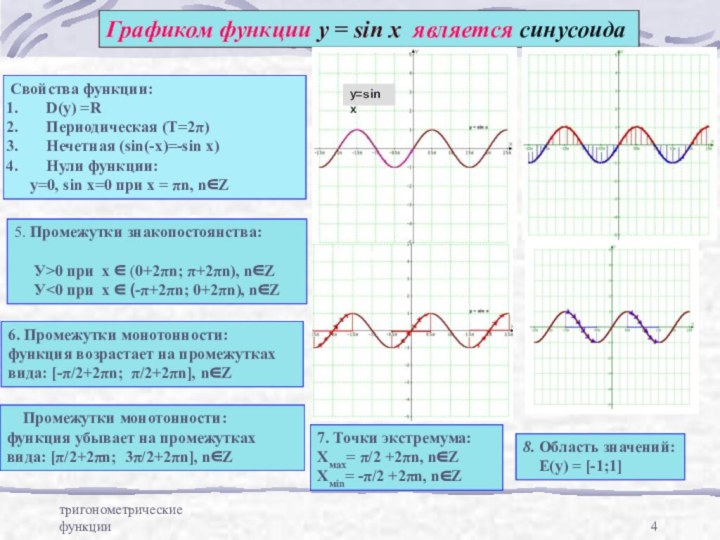
Графиком функции у = sin x является

тригонометрические функцииГрафиком функции у = sin x является синусоидаСвойства функции:D(y) =RПериодическая

синусоида
Свойства функции:
D(y) =R
Периодическая (Т=2π)
Нечетная (sin(-x)=-sin x)
Нули функции:

у=0, sin x=0 при х = πn, n∈Z

y=sin x

5. Промежутки знакопостоянства:

У>0 при х ∈ (0+2πn; π+2πn), n∈Z
У<0 при x ∈ (-π+2πn; 0+2πn), n∈Z

6. Промежутки монотонности:
функция возрастает на промежутках
вида: [-π/2+2πn; π/2+2πn], n∈Z

Промежутки монотонности:
функция убывает на промежутках
вида: [π/2+2πn; 3π/2+2πn], n∈Z

8. Область значений:
Е(у) = [-1;1]

7. Точки экстремума:
Хмах= π/2 +2πn, n∈Z
Хмin= -π/2 +2πn, n∈Z

Слайд 5 тригонометрические функции
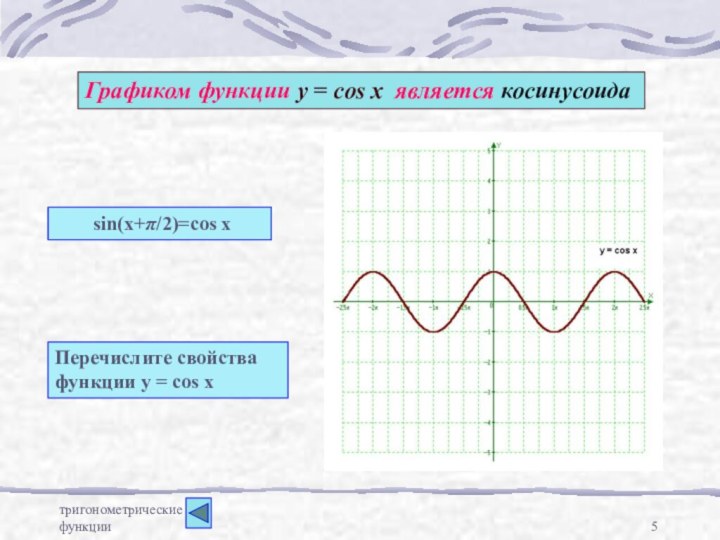
Графиком функции у = cos x является

тригонометрические функцииГрафиком функции у = cos x является косинусоидаПеречислите свойства функции

косинусоида
Перечислите свойства
функции у = cos x
sin(x+π/2)=cos x

Слайд 6 тригонометрические функции
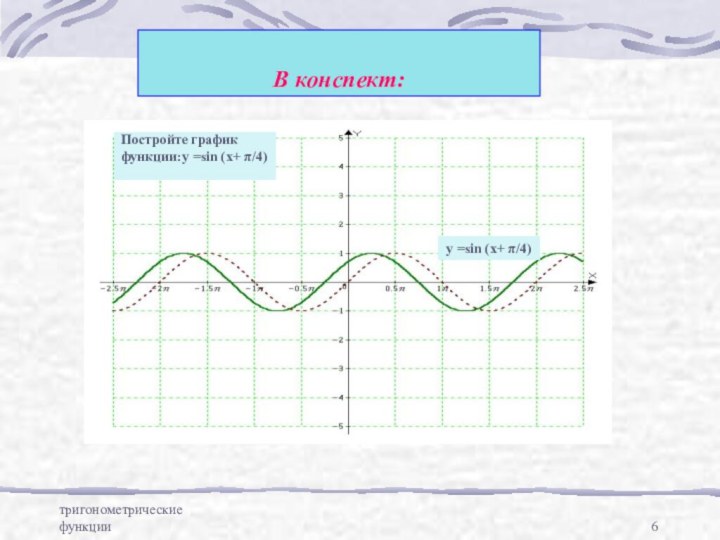
В конспект:
y =sin (x+ π/4)
Постройте график
функции:y

тригонометрические функцииВ конспект:y =sin (x+ π/4)Постройте график функции:y =sin (x+ π/4)

=sin (x+ π/4)

Слайд 7 тригонометрические функции

y =sin (x - π/6)


y =sin (x

тригонометрические функцииy =sin (x - π/6)y =sin (x - π/6)

- π/6)

Слайд 8 тригонометрические функции

В конспект:
y= sin x +π

вспомнить
правила

тригонометрические функцииВ конспект:y= sin x +πвспомнить правила

Слайд 9 тригонометрические функции
В конспект:
График функции у = f (x+в)

тригонометрические функцииВ конспект:График функции у = f (x+в) получается из графика

получается из графика функции у = f(x) параллельным переносом

на (-в) единиц вдоль оси абсцисс
График функции у = f (x)+а получается из графика функции у = f(x) параллельным переносом на (а) единиц вдоль оси ординат


Слайд 10 тригонометрические функции

В конспект:

y=2sinx
y=4sinx
Y=0,5sinx
вспомнить
правила

тригонометрические функцииВ конспект:y=2sinxy=4sinxY=0,5sinxвспомнить правила

Слайд 11 тригонометрические функции
В конспект:
График функции у =k f (x)

тригонометрические функцииВ конспект:График функции у =k f (x) получается из графика

получается из графика функции у = f(x) путем

его растяжения в k раз (при k>1) вдоль оси ординат
График функции у = k f (x) получается из графика функции у = f(x) путем его сжатия в k раз (при 0


Слайд 12 тригонометрические функции

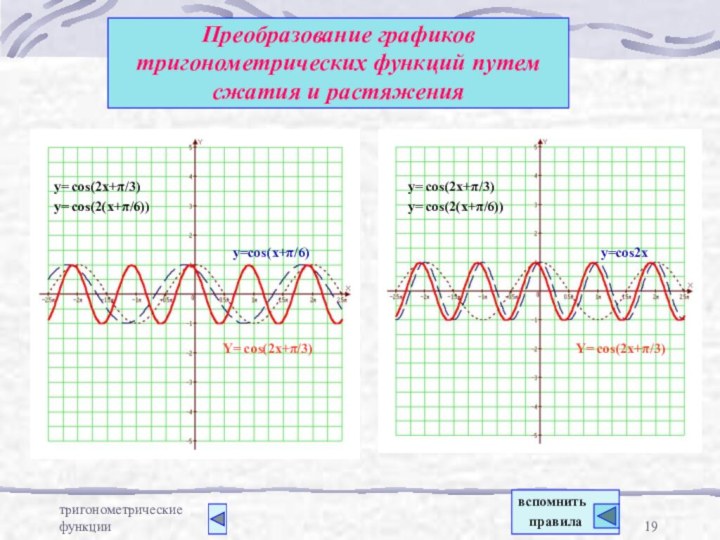
Преобразование графиков тригонометрических функций путем сжатия и

тригонометрические функцииПреобразование графиков тригонометрических функций путем сжатия и растяженияy = cos2xy = cos 0.5xвспомнить правила

растяжения
y = cos2x
y = cos 0.5x
вспомнить
правила

Слайд 13 тригонометрические функции
В конспект:

График функции у = f (kx)

тригонометрические функцииВ конспект:График функции у = f (kx) получается из графика

получается из графика функции у = f(x) путем

его сжатия в k раз (при k>1) вдоль оси абсцисс
График функции у = f (kx) получается из графика функции у = f(x) путем его растяжения в k раз (при 0


Слайд 14 тригонометрические функции
y=2cosx
y=-2cosx

вспомнить
правила

тригонометрические функцииy=2cosxy=-2cosxвспомнить правила

Слайд 15 тригонометрические функции

Преобразование графиков тригонометрических функций путем сжатия и

тригонометрические функцииПреобразование графиков тригонометрических функций путем сжатия и растяженияy = -sin3xy = sin3xвспомнить правила

растяжения
y = -sin3x
y = sin3x
вспомнить
правила

Слайд 16 тригонометрические функции
В конспект:
Графики функций у = -f (kx)

тригонометрические функцииВ конспект:Графики функций у = -f (kx) и у=-k f(x)

и у=-k f(x) получаются из графиков функций у

= f(kx) и y= k f(x) соответственно путем их зеркального отображения относительно оси абсцисс
синус – функция нечетная, поэтому sin(-kx) = - sin (kx)
косинус –функция четная, значит cos(-kx) = cos(kx)


Слайд 17

Слайд 18 ПРАКТИКУМ ( в конспект):
№ № 100(а), 101(а), 102(а),

ПРАКТИКУМ ( в конспект):№ № 100(а), 101(а), 102(а), 103(а)

103(а)

  • Имя файла: prezentatsiya-po-matematike-issledovanie-grafikov-trigonometricheskih-funktsiy.pptx
  • Количество просмотров: 186
  • Количество скачиваний: 1
- Предыдущая Презентация фольклорного праздника Приходи, народ честной, петь и веселиться
Следующая - Презентация по английскому языку : достопримечательности мира

Похожие презентации

Презентация по теме Физический смысл производной Презентация по теме Физический смысл производной 173
Функция у=кх2 ,ее свойства и график Функция у=кх2 ,ее свойства и график 178
Алгебра высказываний. Решение логических задач Алгебра высказываний. Решение логических задач 236
Игра: формулы приведения. 10 класс Игра: формулы приведения. 10 класс 188
Презентация к уроку алгебры на тему Функции(8 класс) Презентация к уроку алгебры на тему Функции(8 класс) 226
Математический диктант по теме Длина дуги Математический диктант по теме Длина дуги 157
График прямой пропорциональности График прямой пропорциональности 153
Готовимся к ОГЭ - 11 (2 часть. Геометрические задачи на вычисление) Готовимся к ОГЭ - 11 (2 часть. Геометрические задачи на вычисление) 187
Презентация по алгебре Предел последовательности Презентация по алгебре Предел последовательности 243
Презентация по алгебре Квадратный корень из степени 8 класс. Презентация по алгебре Квадратный корень из степени 8 класс. 149
Комбинации Комбинации 148
Презентация к уроку Определение производной Презентация к уроку Определение производной 189
Презентация к уроку Великаны и карлики Презентация к уроку Великаны и карлики 158
Метод рационализации Метод рационализации 213
Основы логики Основы логики 223
Функция y = ax². Функция y = ax². 149
Действия над обыкновенными дробями Действия над обыкновенными дробями 150
Линейная функция Линейная функция 162
Презентация по алгебре на тему Преобразование выражений, содержащих квадратные корни (8 класс) Презентация по алгебре на тему Преобразование выражений, содержащих квадратные корни (8 класс) 167
Уравнения с логарифмами Уравнения с логарифмами 148
Целое уравнение и его корни Целое уравнение и его корни 147
Презентация по математике игры Кто хочет стать математикам? Презентация по математике игры Кто хочет стать математикам? 229
Презентация Степень с натуральным показателем. 7 класс. Презентация Степень с натуральным показателем. 7 класс. 154
Решение задач с помощью пропорций Решение задач с помощью пропорций 155
Презентация по алгебре на тему Прогрессии (9 класс) Презентация по алгебре на тему Прогрессии (9 класс) 154
ЭОР по теме Целые уравнения . Алгебра .9 класс. ЭОР по теме Целые уравнения . Алгебра .9 класс. 163
Графическое решение уравнений Графическое решение уравнений 161
Презентация по теме Логарифмы 9класс Презентация по теме Логарифмы 9класс 193
Приращение аргумента. Приращение функции Приращение аргумента. Приращение функции 186
Презентация Повторение и расширение понятия функции (9 класс) Презентация Повторение и расширение понятия функции (9 класс) 427