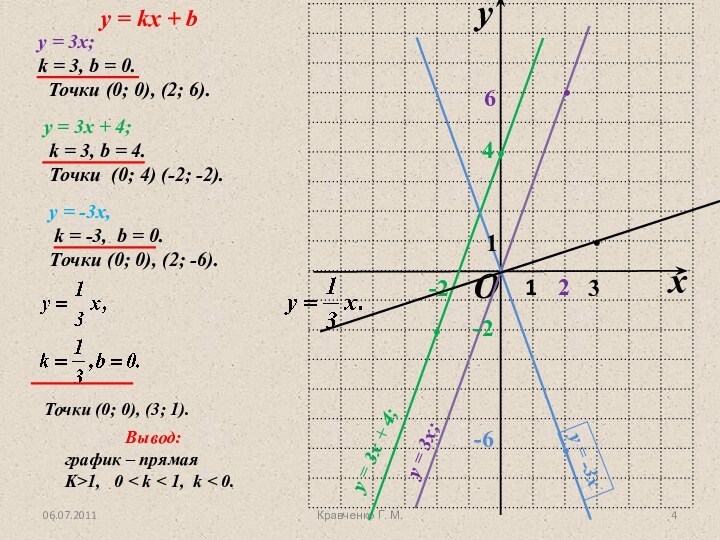
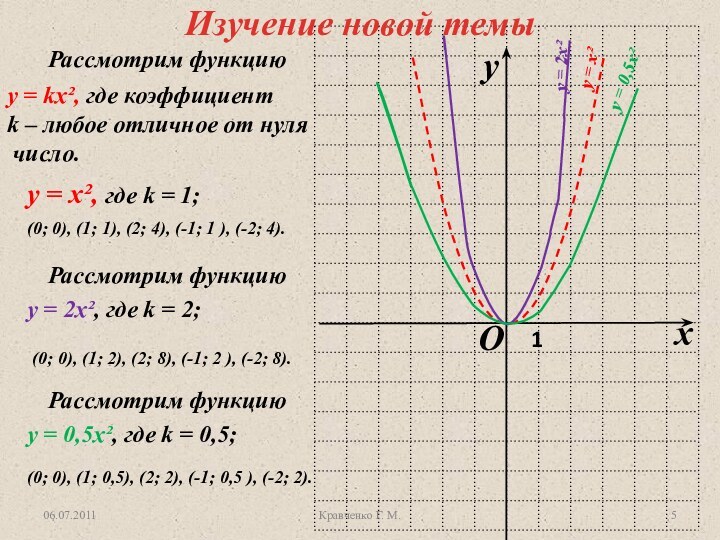
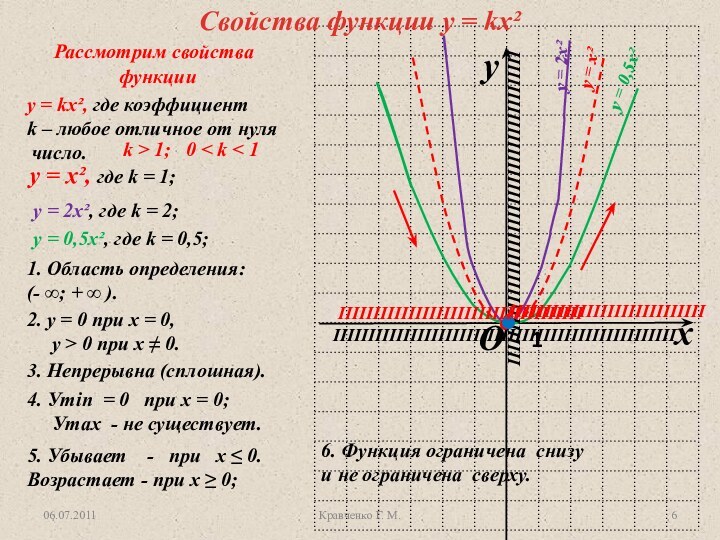
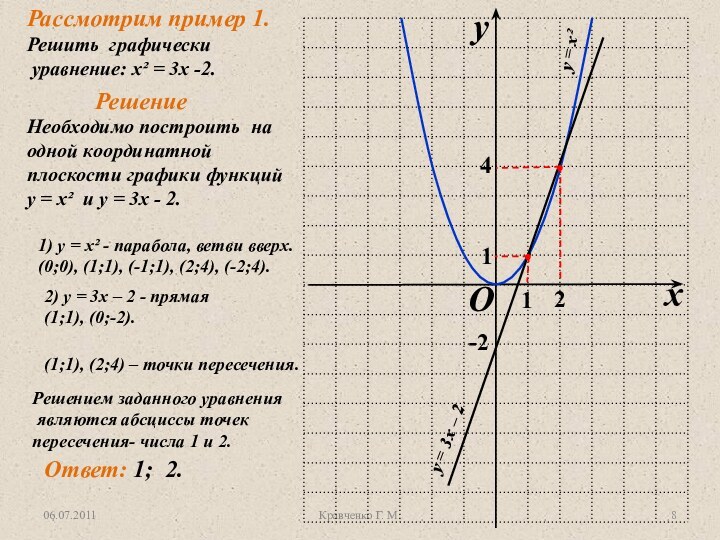
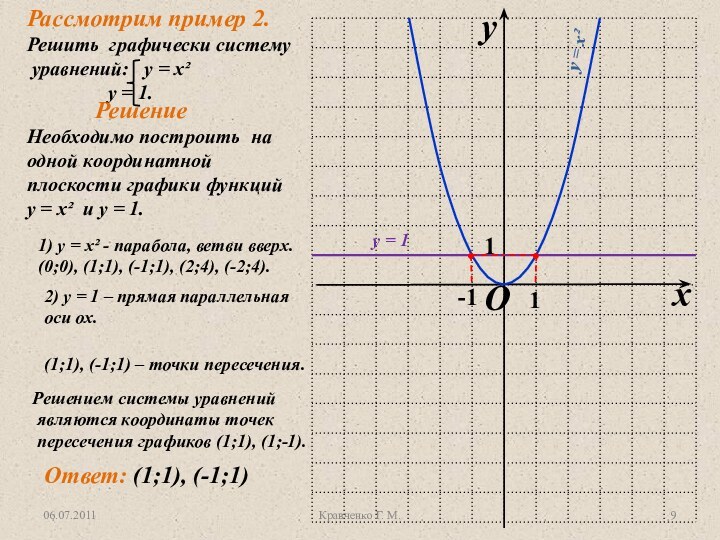
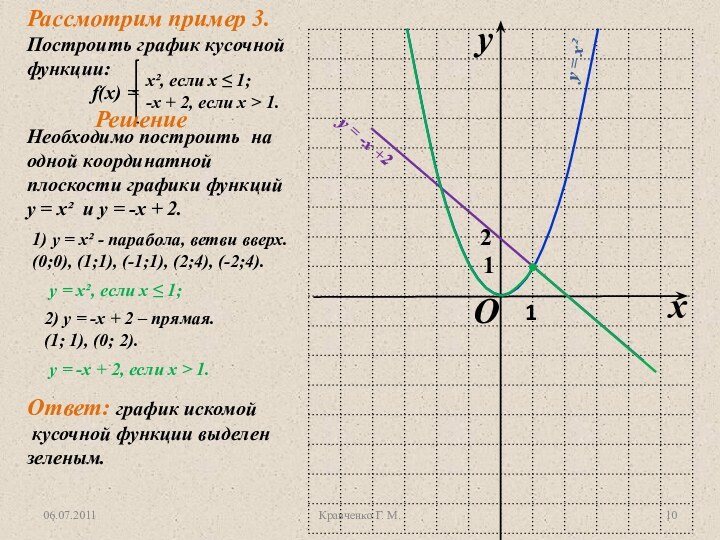
у = х², их графики.
Изучить свойства функции у =
kx², у = - kx² и научиться строить график.Научиться по графику определять свойства данных функций.
Ввести правила решения уравнений графическим способом.
Изучить способ построения графиков функций, заданных несколькими условиями.
Цели:
06.07.2011
Кравченко Г. М.