Слайд 3
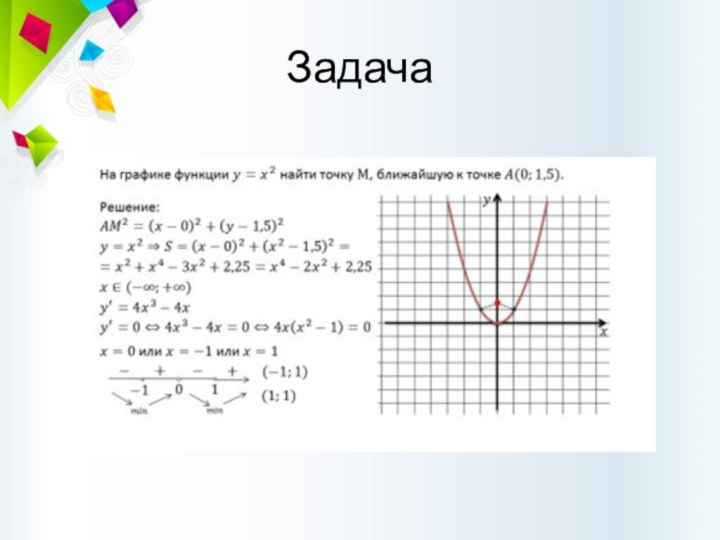
Задача
Таня очень любит возиться с цветами. Поэтому родители
на даче выделили место под клумбу. Огородить клумбу они
решили декоративным забором. Таня решила сделать клумбу прямоугольной формы. У неё есть двадцать метров забора. Давайте поможем Тане определиться со сторонами прямоугольника, чтобы площадь клумбы была наибольшей.
Для начала давайте изобразим прямоугольник. Обозначим его стороны за а и b. И запишем известные нам факты.
Слайд 4
Тогда наша задача сводиться к нахождению наибольшей площади.
То есть, если мы формулу для вычисления площади примем
за функцию с аргументом а и функцией S, то наша задача сводится к нахождению наибольшего значения функции. Теперь давайте определимся с промежутком, в котором будет изменяться значения аргумента функции. Очевидно, что стороной прямоугольника может быть число от 0 до 10.
Теперь применим алгоритм отыскания наибольшего значения функции на промежутке.
Слайд 5
Задачи такого типа называют задачами на оптимизацию. То
есть нам надо найти такие значения неких переменных, при
которых другие зависящие от них переменные принимают наибольшие или наименьшие значения.
Слайд 6
Схема решения задач на оптимизацию
основную схему решения задач
на оптимизацию.