неравенств
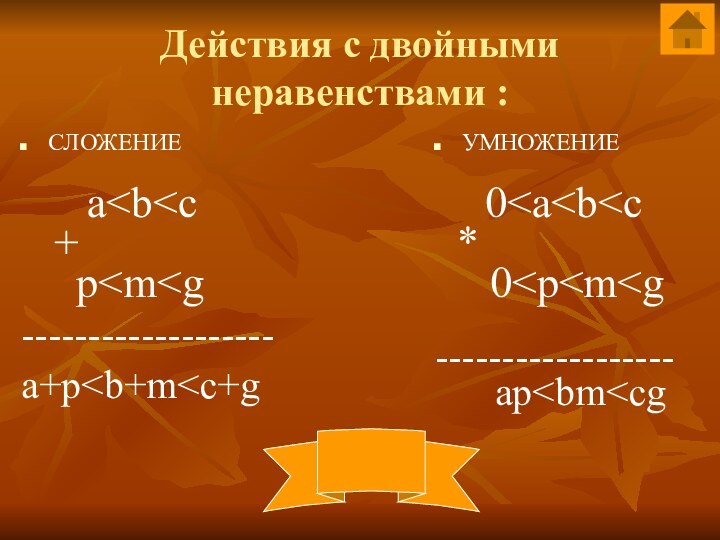
Действия с двойными
неравенствами
Доказательства
неравенств
Решение
линейныхнеравенств
Система линейных
неравенств
Решение системы
линейных неравенств
Дидактический
материал по теме
Контрольные вопросы
по теме