- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Квадратные уравнения (8 класс)
Содержание
- 2. Цель работы: Познакомиться с биографией великих
- 3. введение Человеку, изучающему алгебру, часто полезнее решить одну
- 4. История возникновения и развития квадратных уравнений
- 5. Древний Вавилон
- 9. : 1) «Квадраты равны корням», т.е. аx²
- 11. Франсуа Виет (1540-1603) первым
- 12. Люди, благодаря которым способ решения квадратных
- 13. Что такое квадратное уравнение?Квадратное уравнение – уравнение
- 14. Способы решений квадратных уравнений.
- 15. 1 способ: разложение левой части уравнения на
- 16. 2 способ: выделение квадрата двучлена. Цель
- 17. Пример 1
- 18. 3 cпособ: решение квадратных уравнений по формуле.
- 19.
- 24. 4 cпособ: решение квадратных уравнений с
- 26. 5 cпособ: решение квадратных уравнений способом «переброски».
- 27. Пример 1:
- 28. 6 cпособ: свойства коэффициентов квадратного уравнения.
- 31. 7 способ: графический способ решения квадратных уравнений.Решим
- 32. Возможны следующие случаи: Прямая и парабола могут
- 33. Пример:x2 – х – 2 = 0x
- 34. 8 cпособ: геометрический способ (основан на выделении полного квадрата).Решить уравнение х2+ 10х =39
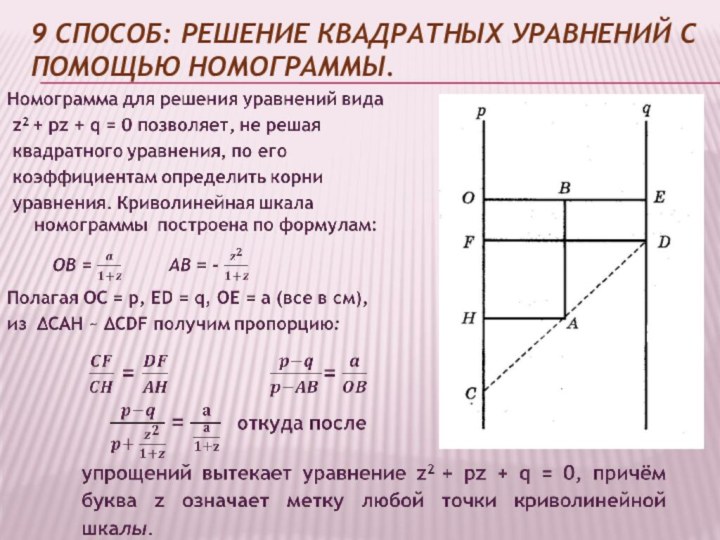
- 35. 9 способ: решение квадратных уравнений с помощью номограммы.
- 36. Примеры : Для уравнения z2 -
- 37. Для уравнения z2 + 5z –
- 39. Для уравнения z2 - 25z + 66
- 40. Заключение
- 41. В результате выполнения работы были изучены следующие
- 42. Скачать презентацию
- 43. Похожие презентации
Цель работы: Познакомиться с биографией великих математиков, занимавшихся решением квадратных уравнений. Найти различные способы решений квадратных уравнений. Рассмотреть практическое применение способов решения квадратных уравнений в современной жизни.





































Слайд 2
Цель работы:
Познакомиться с биографией великих математиков, занимавшихся решением
квадратных уравнений.
способов решения квадратных уравнений в современной жизни.
Слайд 3
введение
Человеку, изучающему алгебру, часто полезнее решить одну и
ту же задачу тремя различными способами, чем решать три-четыре
задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт.У.У. Сойер (английский математик XX века)
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Умение решать уравнения не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям.
Слайд 4
История возникновения и развития квадратных уравнений
Кто хочет ограничиться настоящим
без знания прошлого, тот никогда его не поймет.Г.В. Лейбниц
(немецкий математик XVII-XVIII веков)
Слайд 6
индия
Индийский ученый, Брахмагупта (VII век),
изложил общее правило решения квадратных уравнений, приведенных к единой конической форме: ах2 + bx = c, где a > 0. В этом уравнении коэффициенты (кроме а) могут быть и отрицательными.
Брахмагупта
Слайд 7
Древняя Греция
Приемы решения уравнений без обращения к геометрии дает
Диофант Александрийский (III в.). В его книгах «Арифметика» нет систематического изложения алгебры, однако в них содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений различных степеней. При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.Слайд 8
Средняя Азия
Основоположником алгебры считают среднеазиатского математика Мухаммед бен
Муса аль - Хорезми (787 – 850 г. г.).Аль-Хорезми написал сочинение, которое по-арабски называется «Китаб аль-джебр валь-мукабала» . Это сочинение оказало большое влияние на развитие математики в Европе, а само слово «аль-джебр», входившее в название книги, постепенно стало названием науки - алгебра.
Слайд 9
:
1) «Квадраты равны корням», т.е. аx² = bх.
2) «Квадраты равны числу», т.е.
аx² = с.3) «Корни равны числу», т.е. bx = с.
4) «Квадраты и числа равны корням», т.е. аx² + с = bх.
5) «Квадраты и корни равны числу», т.е. аx² + bx = с.
6) «Корни и числа равны квадратам», т.е. bx + с = аx².
Слайд 10
Европа
Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. в «Книге абака» итальянским математиком Леонардом Фибоначчи. Он первый в Европе подошел к введению отрицательных чисел.
Леонард Фибоначчи
Слайд 11 Франсуа Виет (1540-1603) первым догадался
обозначать буквами не только неизвестные, но и коэффициенты при
них. Это скромное, казалось бы, новшество внесло огромный вклад в развитие математики. Ведь если не использовать букв для обозначения коэффициентов квадратного уравнения, то записать даже несложную формулу для его решения будет довольно трудно. Недаром Виета часто называют «отцом алгебры».
Франсуа Виет
Слайд 12 Люди, благодаря которым способ решения квадратных уравнений принимает
современный вид
Декарт
Жиррар Ньютон
Слайд 13
Что такое квадратное уравнение?
Квадратное уравнение – уравнение вида
ax2 + bx + c = 0,
где х- переменная,
а,b и с-некоторые числа, причем, а ≠ 0.Приведенные квадратные уравнения – это уравнения вида
x2 + px + q = 0, в котором старший коэффициент a=1.
Если в квадратном уравнении
ах2 + bx + c = 0
хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.
Неполные квадратные уравнения бывают трёх видов:
1) ах2 + с = 0, где b = 0;
2) ах2 + bх = 0, где с = 0;
3) ах2 = 0, где b = c = 0.
Слайд 15
1 способ: разложение левой части уравнения на множители.
x2 +10x – 24 = 0
x2 + 12x – 2x – 24 = 0x (x - 2 ) + 12( x - 2) = 0
(x-2)(x+12) = 0
x – 2 = 0 или x + 12 = 0
x = 2 или x = - 12
Ответ: х1 = 2; х2 = - 12
Этот метод не всегда удобен, т.к. не всегда удается применить способ группировки.
Слайд 16
2 способ: выделение квадрата двучлена.
Цель метода -
привести уравнение общего вида к неполному квадратному уравнению. В
этом нам помогут формулы сокращенного умножения, а именно, квадратов суммы и разности:Этот метод применим для любых квадратных уравнений, но очень громоздкий, поэтому не всегда удобен. Используется для доказательства формулы корней квадратного уравнения и при решении более сложных задач.
(а + b)2 = a2 + 2ab + b2;
(a – b)2 = a2 – 2ab + b2.
Слайд 24 4 cпособ: решение квадратных уравнений с использованием теоремы
Виета.
Теорема: Сумма корней приведённого квадратного уравнения равна второму коэффициенту,
взятому с противоположным знаком, а произведение корней равно свободному члену, т. е. х²+ px + q = 0
х1 · х2 = q
x1 + x2 = - p
Слайд 31
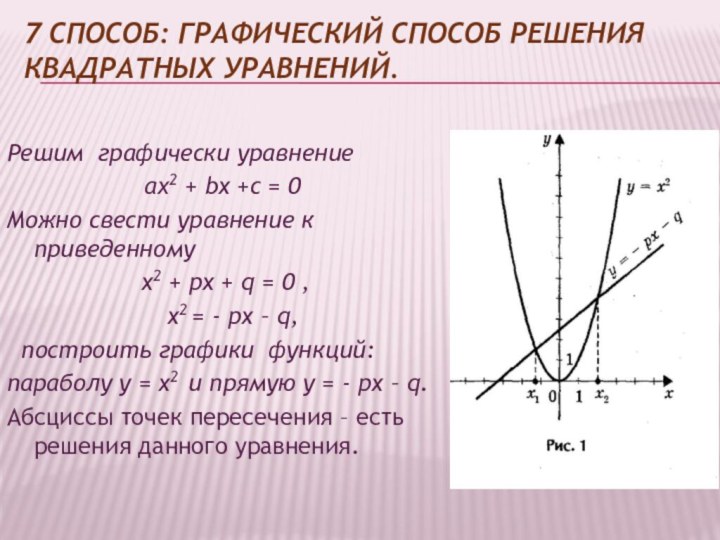
7 способ: графический способ решения квадратных уравнений.
Решим графически
уравнение
ах2 + bx +с = 0
Можно свести уравнение к приведенному
x2 + px + q = 0 , x2 = - px – q,
построить графики функций:
параболу y = x2 и прямую y = - px – q.
Абсциссы точек пересечения – есть решения данного уравнения.
Слайд 32
Возможны следующие случаи:
Прямая и парабола могут пересекаться
в двух точках, абсциссы точек пересечения являются корнями квадратного
уравнения.Прямая и парабола могут касаться (только одна общая точка), т. е. уравнение имеет одно решение.
Прямая и парабола не имеют общих точек,
т. е. квадратное уравнение не имеет корней.
Слайд 33
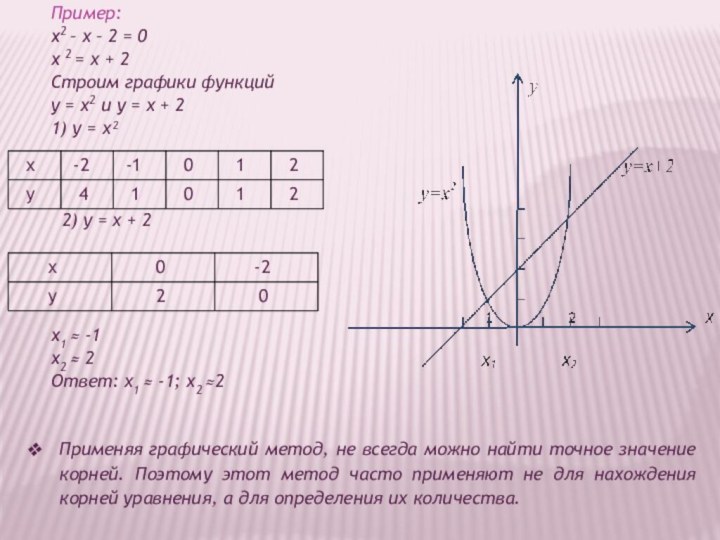
Пример:
x2 – х – 2 = 0
x 2
= х + 2
Строим графики функций
y = х2
и y = х + 21) у = х²
2) у = х + 2
x1 ≈ -1
x2 ≈ 2
Ответ: х1 ≈ -1; х2 ≈2
Применяя графический метод, не всегда можно найти точное значение корней. Поэтому этот метод часто применяют не для нахождения корней уравнения, а для определения их количества.
Слайд 34 8 cпособ: геометрический способ (основан на выделении полного
квадрата).
Решить уравнение х2+ 10х =39
Слайд 36
Примеры :
Для уравнения z2 - 9z +
8 = 0 номограмма даёт корни z1 =
8 и z2 = 1Решим с помощью номограммы уравнение
2z2 - 9z + 2 = 0
Разделим коэффициенты этого уравнения на 2, получим уравнение
z2 - 4,5z + 1 = 0
Номограмма даёт корни z1 = 4 и z2 = 0,5
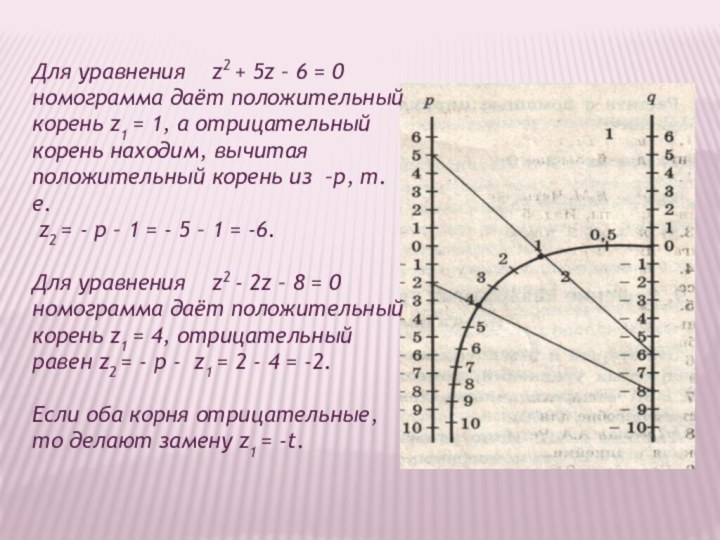
Слайд 37 Для уравнения z2 + 5z – 6
= 0 номограмма даёт положительный корень z1 = 1,
а отрицательный корень находим, вычитая положительный корень из –р, т. е.z2 = - p – 1 = - 5 – 1 = -6.
Для уравнения z2 - 2z – 8 = 0 номограмма даёт положительный корень z1 = 4, отрицательный равен z2 = - р - z1 = 2 - 4 = -2.
Если оба корня отрицательные, то делают замену z1 = -t.
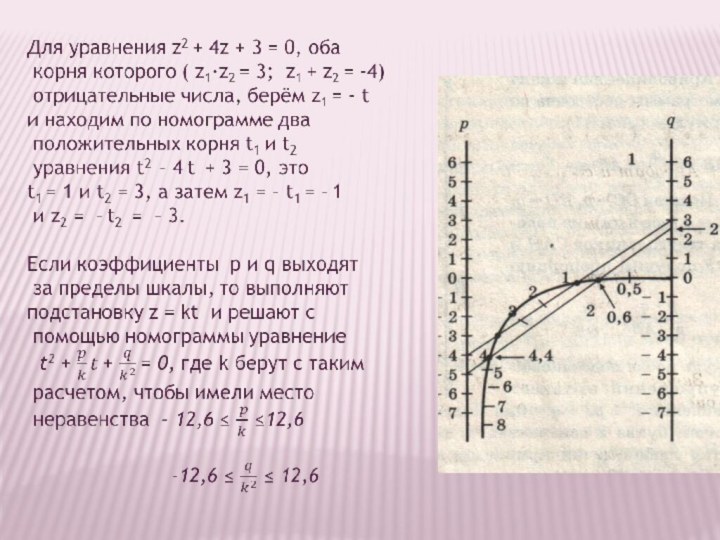
Слайд 39 Для уравнения z2 - 25z + 66 =
0 коэффициенты p и q выходят за пределы шкалы,
выполним подстановку z =5t, получим:t2 - 5t + 2, 64 = 0,
которое решаем посредством номограммы и получим:
t1 = 0,6 и t2 = 4,4
откуда z1 = 5t 1= 5·0,6 = 3
z2 = 5t2 = 5·4,4 = 22
Слайд 41
В результате выполнения
работы были изучены следующие способы:
1.Разложение левой части уравнения на множители.
2. Выделение квадрата двучлена.3.Решение квадратных уравнений по формуле.
4.С помощью теоремы Виета.
5.Решение квадратных уравнений способом «переброски».
6.Свойства коэффициентов квадратного уравнения.
7.Графический способ решения квадратных уравнений.
8. Геометрический метод.
9.Решение квадратных уравнений с помощью номограммы.
Каждый из изученных способов имеет как положительные стороны, так и недостатки. Но выполненная работа показывает, что использование различных способов при решении квадратных уравнений является важным звеном в изучении математики, развивает внимание и сообразительность. Так же не менее важно умение правильно выбирать рациональный способ решения конкретно для каждого уравнения.





























