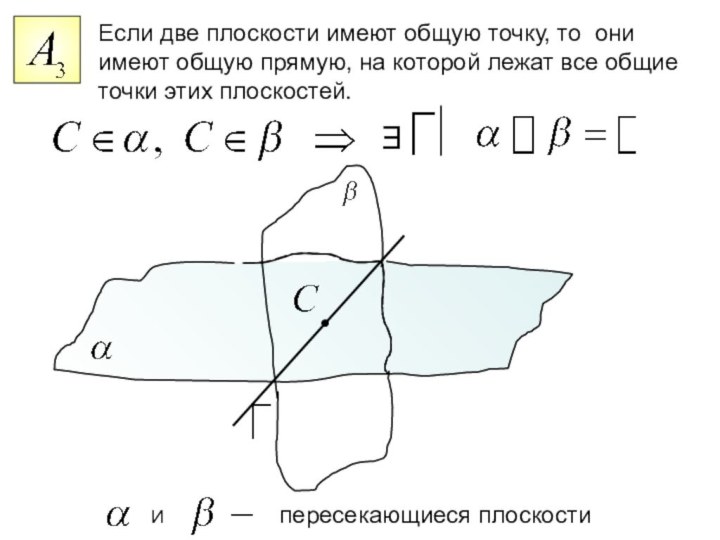
имеют общую прямую, на которой лежат все общие
точки этих
плоскостей. Ǝ
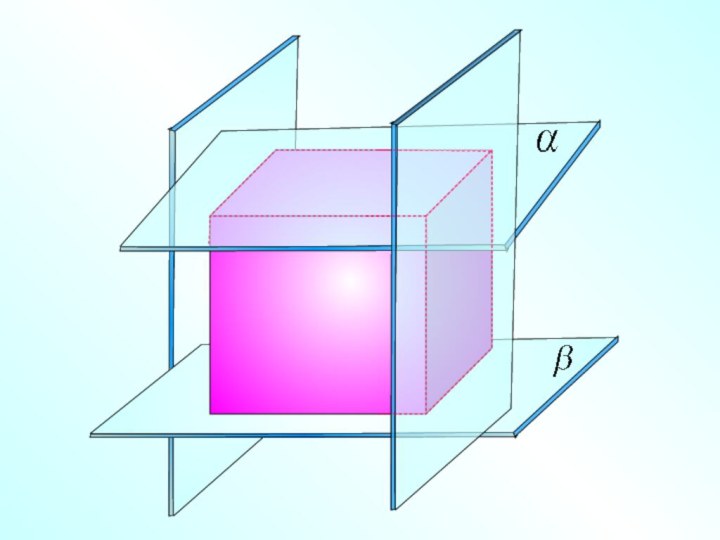
И пересекающиеся плоскости
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть









Ǝ
И пересекающиеся плоскости
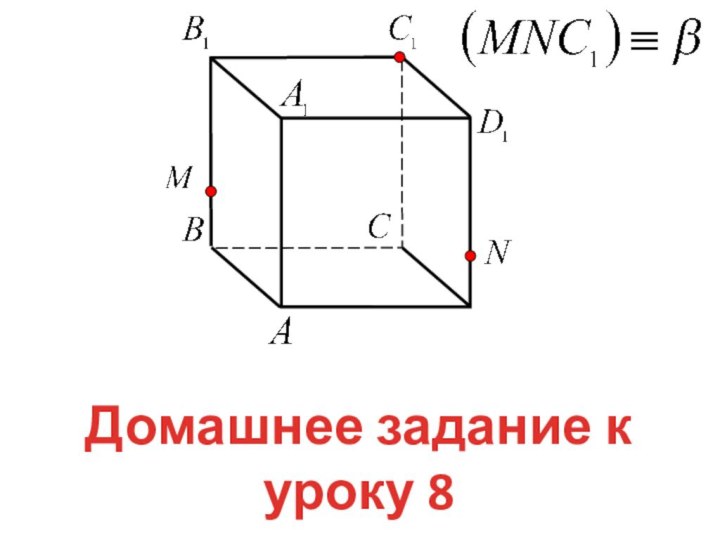
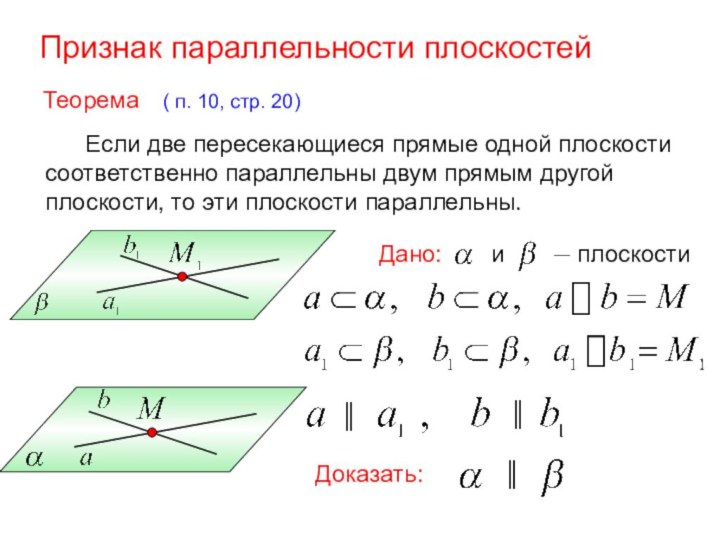
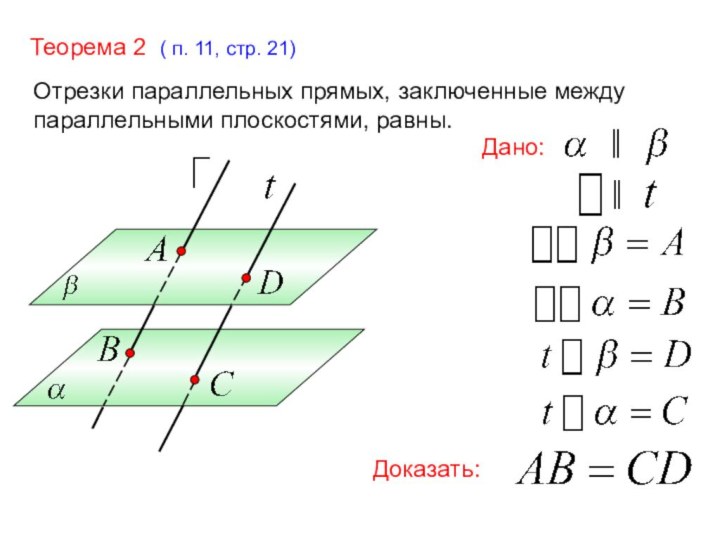
Дано:
и плоскости
║
║
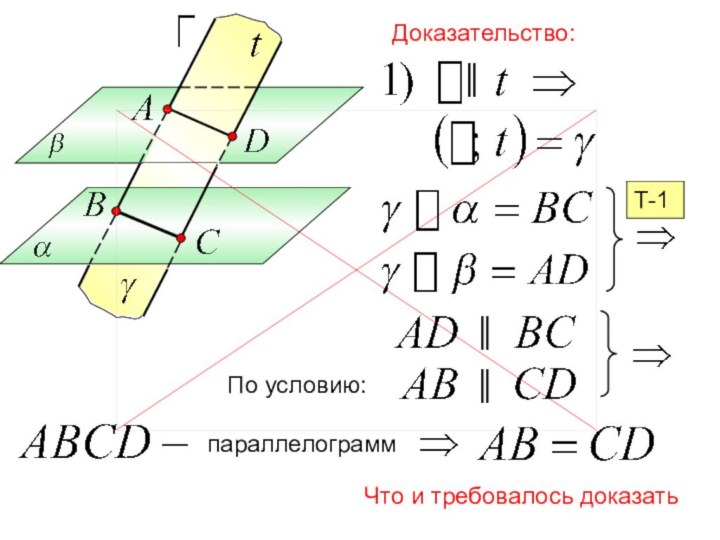
Доказать:
║
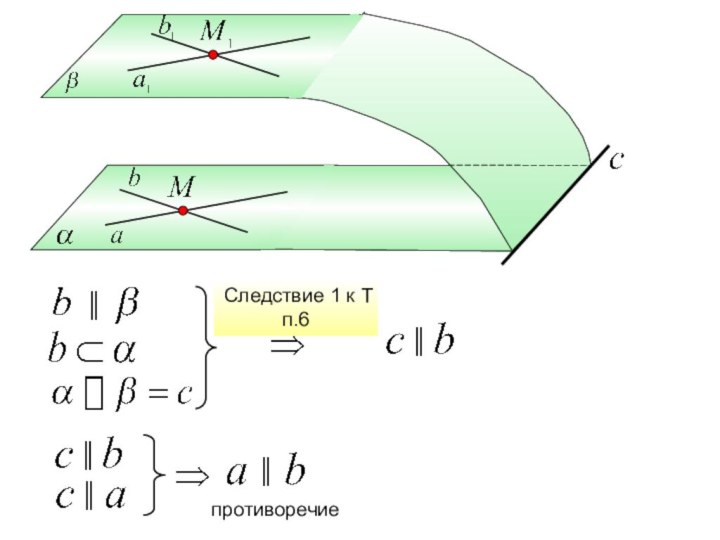
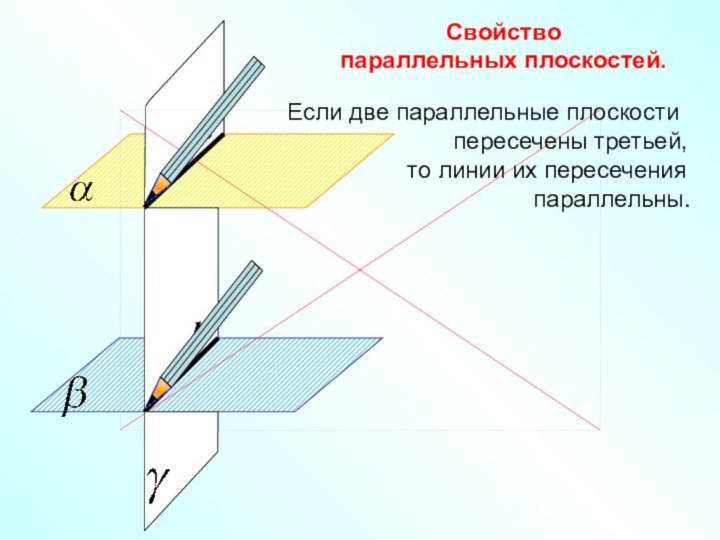
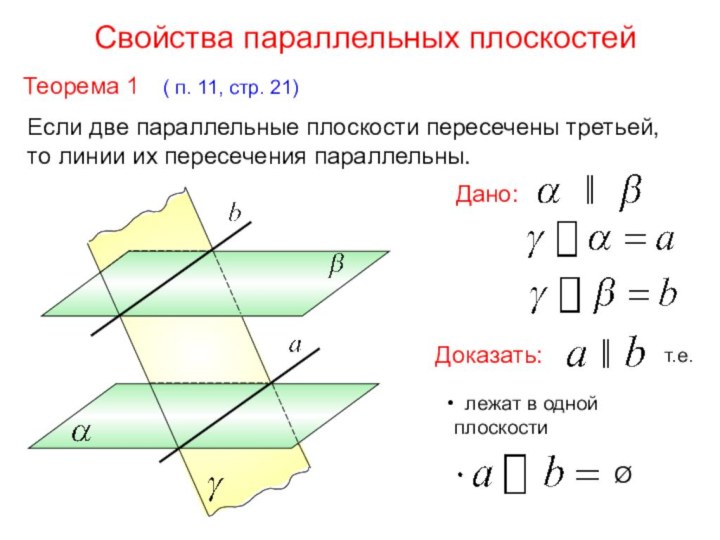
Свойство
параллельных плоскостей.
Дано:
Доказать:
║
║
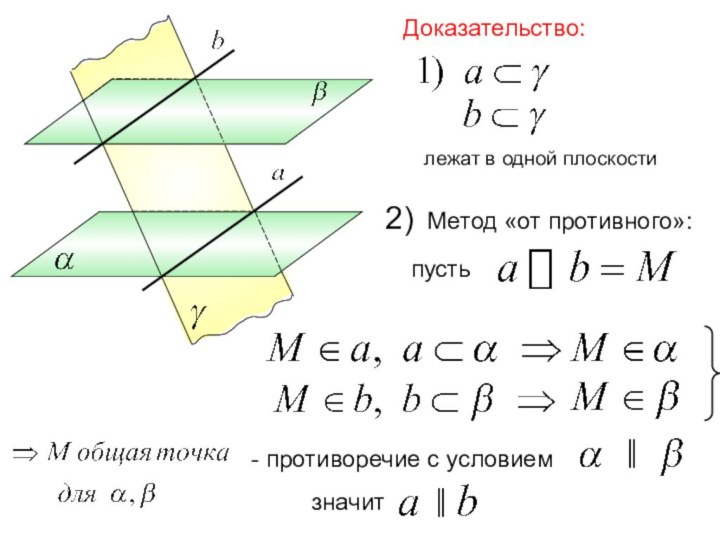
лежат в одной плоскости
т.е.
Ø