- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре: Понятие действительного числа
Содержание
- 2. Работа в парах
- 3. Второй вариант актуализации темыОтрицательные числаПоложительные Обыкновенные дробинульДробные числарациональныецелыеиррациональныеДесятичные дробиКонечные десятичные дробиДействительные числаБесконечные период.десятичные дроби
- 4. Числовые множества1,2,3,4,5,6…… , -3,-2,-1,0,1,2,3, …NRZМножество натуральных чиселМножество действительных чиселМножество рациональных чиселМножество целых чиселМножество иррациональных чисел
- 5. Числовые множества1,2,3,4,5,6…… , -3,-2,-1,0,1,2,3, …NRZМножество натуральных чиселМножество действительных чиселМножество рациональных чиселМножество целых чиселМножество иррациональных чисел
- 6. Числовые множества1,2,3,4,5,6…… , -3,-2,-1,0,1,2,3, …NRZМножество натуральных чиселМножество действительных чиселМножество рациональных чиселМножество целых чиселМножество иррациональных чисел
- 7. Диаграммы ЭйлераR-действительные числаI-иррациональные числаQ-рациональные числаZ-целые числаN-натуральные числа
- 9. Обозначение
- 10. N. Натуральными числами называются числа, которые используются
- 11. Множество натуральных чиселНатуральные числа - это числа
- 12. Z. Целое число – это расширение множества
- 13. Множество целых чисел.Введем в рассмотрение новые числа:
- 14. Иррациональное число может быть представлено в виде бесконечной непериодической дроби.
- 15. Множество иррациональных чисел.Числа, которые представляются бесконечной непериодической
- 17. Множество рациональных чисел.Множество рациональных чисел можно представить
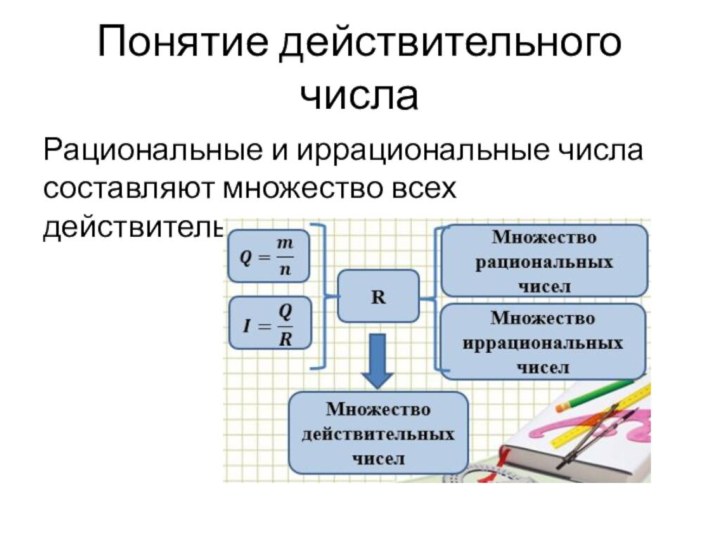
- 19. Понятие действительного числаРациональные и иррациональные числа составляют множество всех действительных чисел.
- 20. Но в множестве рациональных чисел нельзя, например,
- 21. Скачать презентацию
- 22. Похожие презентации
Работа в парах
















Слайд 3
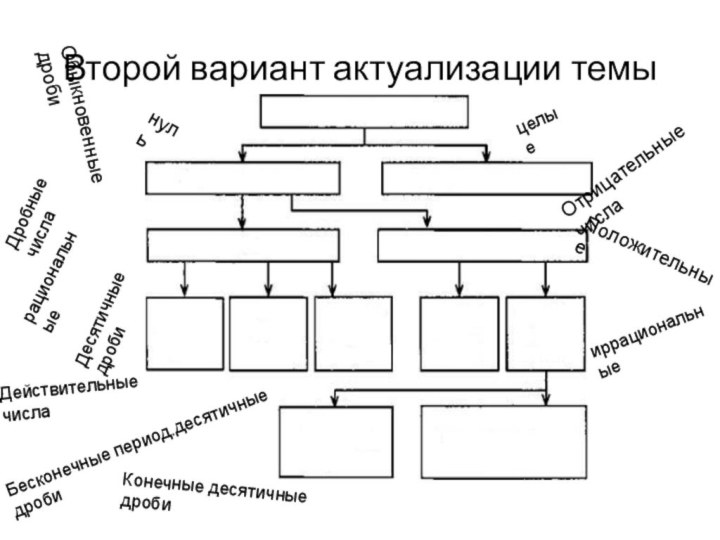
Второй вариант актуализации темы
Отрицательные числа
Положительные
Обыкновенные дроби
нуль
Дробные числа
рациональные
целые
иррациональные
Десятичные
дроби
Слайд 4
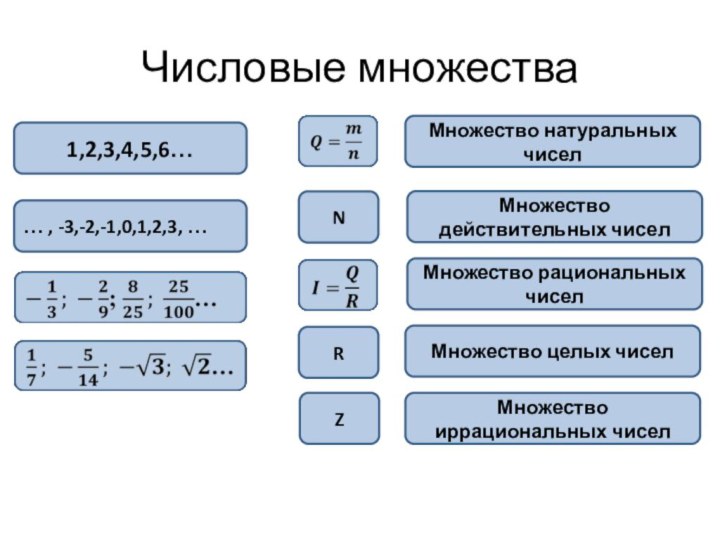
Числовые множества
1,2,3,4,5,6…
… , -3,-2,-1,0,1,2,3, …
N
R
Z
Множество натуральных чисел
Множество действительных
чисел
Множество рациональных чисел
Множество целых чисел
Множество иррациональных чисел
Слайд 5
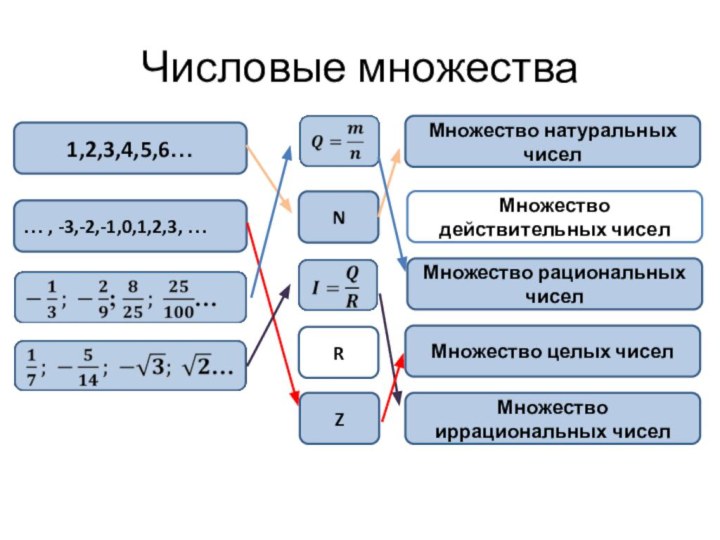
Числовые множества
1,2,3,4,5,6…
… , -3,-2,-1,0,1,2,3, …
N
R
Z
Множество натуральных чисел
Множество действительных
чисел
Множество рациональных чисел
Множество целых чисел
Множество иррациональных чисел
Слайд 6
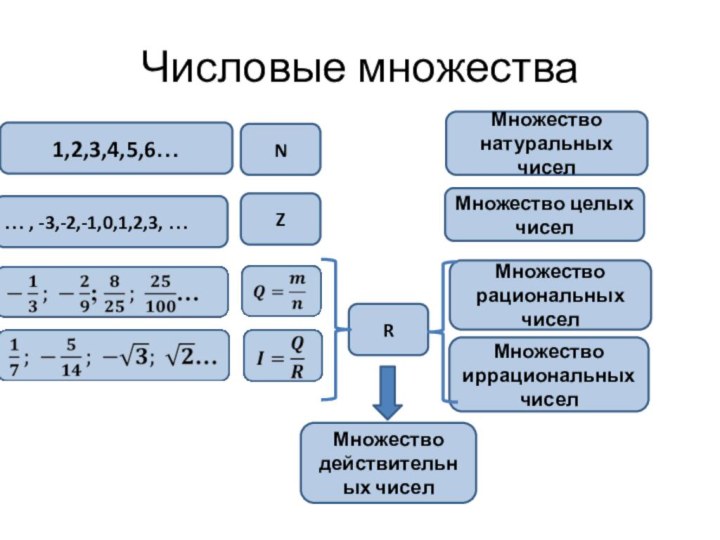
Числовые множества
1,2,3,4,5,6…
… , -3,-2,-1,0,1,2,3, …
N
R
Z
Множество натуральных чисел
Множество действительных
чисел
Множество рациональных чисел
Множество целых чисел
Множество иррациональных чисел
Слайд 7
Диаграммы Эйлера
R-действительные числа
I-иррациональные числа
Q-рациональные числа
Z-целые числа
N-натуральные числа
Слайд 9 Обозначение Название
множества
N
Множество натуральных чиселZ Множество целых чисел
Q=m/n Множество рациональных чисел
I=R/Q Множество иррациональных чисел
R Множество вещественных чисел
Числовые множества
Слайд 10 N. Натуральными числами называются числа, которые используются при
счете или для указания порядкового номера предмета среди однородных
предметов. Или, натуральные числа, это числа от 1, до + бесконечности.
Слайд 11
Множество натуральных чисел
Натуральные числа - это числа счета.
N={1,2,…n,…}.
Заметим, что множество натуральных чисел замкнуто относительно сложения и
умножения, т.е. сложение и умножение выполняются всегда, а вычитание и деление в общем случае не выполняютсяСлайд 12 Z. Целое число – это расширение множества натуральных
чисел, получаемое добавлением к нему нуля и отрицательных чисел.
Слайд 13
Множество целых чисел.
Введем в рассмотрение новые числа:
1) число 0 (ноль),
2) число (-n), противоположное
натуральному n.При этом полагаем: n+(-n)=(-n)+n=0,
-(-n)=n.
Тогда множество целых чисел можно записать так:
Z ={…,-n,…-2,-1,0,1,2,…,n,…}.
Заметим также, что:
Это множество замкнуто относительно сложения, вычитания и умножения, т.е.
Из множества целых чисел выделим два подмножества:
1) множество четных чисел
2) множество нечетных чисел
Слайд 15
Множество иррациональных чисел.
Числа, которые представляются бесконечной непериодической дробью,
будем называть иррациональными.
Множество иррациональных чисел обозначим
I.Для иррациональных чисел нет единой формы обозначения. Отметим два иррациональных числа, которые обозначаются буквами – это числа π и е.
Слайд 17
Множество рациональных чисел.
Множество рациональных чисел можно представить в
виде:
В частности,
Таким образом, Множество рациональных чисел замкнуто относительно сложения, вычитания, умножения и деления (кроме случая деления на 0).
Слайд 19
Понятие действительного числа
Рациональные и иррациональные числа составляют множество
всех действительных чисел.
Слайд 20 Но в множестве рациональных чисел нельзя, например, измерить
гипотенузу прямоугольного треугольника с катетам
.По теореме Пифагора гипотенуза будет равна .
Но число не будет рациональным, так как ни для каких m и n.
Нельзя решить уравнение .
Нельзя измерить длину окружности и т.д.
Заметим, что всякое рациональное число можно представить в виде конечной или бесконечной периодической десятичной дроби.





























