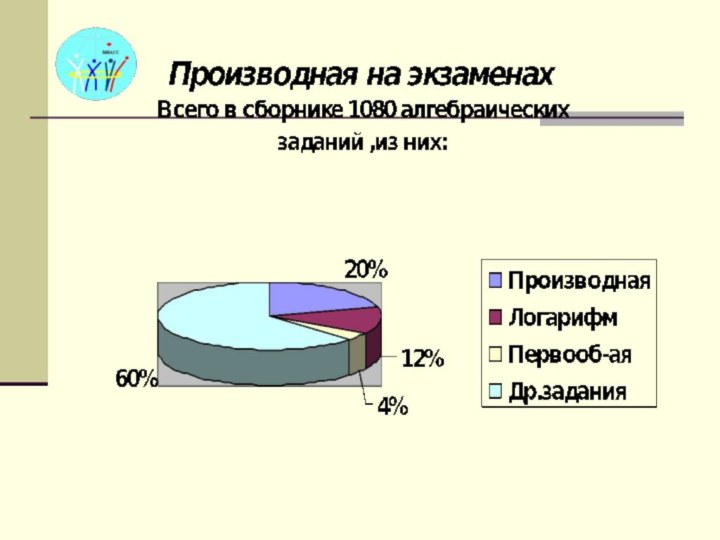
Презентация на тему по математике на тему Производная элементарных функций (10 класс)

правила дифференцирования.
2. Развивать познавательный интерес к теме «Дифференцирование»
3. Воспитывать

стремление давать лаконично ответы на вопросы.

на математическом языке. Производная помогает нам успешно решать не

только математические задачи, но и задачи практического характера в разных областях науки и техники»

бесконечно малых стало началом больших преобразований. Но наряду с

интегральными методами складывались и методы дифференциальные. Вырабатывались элементы будущего дифференциального исчисления при решении задач, которые в настоящее время и решаются с помощью дифференцирования. В то время такие задачи были трех видов: определение касательных к кривым, нахождение максимумов и минимумов функций, отыскивание условий существования алгебраических уравнений квадратных корней.

Ньютоном и Лейбницем в конце 17 столетия на основе

двух задач: 1) о разыскании касательной к произвольной линии; 2) о разыскании скорости при произвольном законе движения; Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.

Исаак Ньютон (1643-1727) один из создателей

дифференциального исчисления.
Главный его труд- «Математические начала натуральной философии».-оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.
Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.

наук. Основоположник дифференциального исчисления, ввёл большую часть современной

символики математического анализа.
Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл .

…что до них эти вопросы

не изучались. Задолго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции.

на основе учения Г.Галилея активно развилась кинематическая концепция производной.

Понятие производной встречается уже у Р.Декарта, французского математика Роберваля, английского учёного Д.Грегори, в работах И.Барроу.
Но систематическое учение с выдвижением двух основных проблем математического анализа развито Ньютоном и Лейбницем.

практические задачи в механике и геометрии, пришли к одному

понятию – «производная», показав тем самым, что дифференциальное исчисление- это есть окружающая действительность, переложенная на математический язык.

базируется на понятии предела, которое было дано (наряду с

другими важнейшими понятиями – непрерывность, интеграл и т.д.) в работах французского математика Огюстена Луи Коши.

Огюстен Луи Коши

основе учения Г.Галилея о движении активно развивалась кинематическая концепция

производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

Декарт

похожие части слова, да и смысл похож: производная происходит

от исходной функции (переложив на отношения человека: исходная функция- «мама»,её производная «дочь»).Производная- часть математической науки, одно из её звеньев. Нет этого звена - прерваны связи между многими понятиями.

- это скорость. С геометрической производная -

это тангенс угла наклона (угловой коэффициент) касательной. С точки зрения практического анализа производная функции - это функция, которая отвечает за ее (функции ) возрастание и убывание.

(т.е. имеют производную) почти в каждой точке своей области

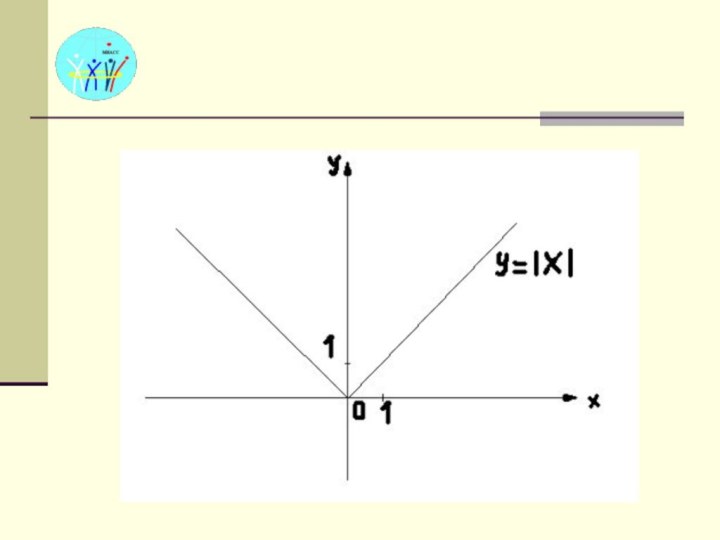
определения. Встречаются ли в жизни недифференцируемые функции? Да, встречаются. В геометрии это кривые с «углами», вроде графика функции: модуль x, в точке xo=0.В физике это движение упругого мячика, брошенного в стену, в момент отскока, или шайбы, отскакивающей от бортика.

при вращении параболы вокруг своей оси, называется параболоидом вращения.

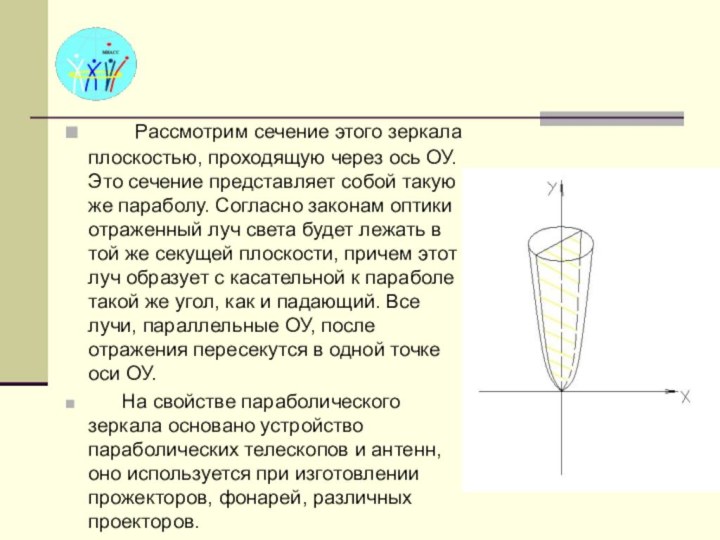
Представим себе, что его внутренняя поверхность зеркальная и это параболическое зеркало освещается пучком лучей света, параллельно оси ОУ.
 

проходящую через ось ОУ. Это сечение представляет собой такую

же параболу. Согласно законам оптики отраженный луч света будет лежать в той же секущей плоскости, причем этот луч образует с касательной к параболе такой же угол, как и падающий. Все лучи, параллельные ОУ, после отражения пересекутся в одной точке оси ОУ.
На свойстве параболического зеркала основано устройство параболических телескопов и антенн, оно используется при изготовлении прожекторов, фонарей, различных проекторов.

Производная успешно применяется при решении различных прикладных задач в науке, технике и жизни.

были одними из первых приложений для вычислительных машин. Формальное

дифференцирование было реализовано на ранних этапах развития вычислительной техники в 1953 году.

;
f(x)=e-4-2x+ln(0.5ex).


2 вариант
f(x)=5x-8;
g(x)=cosx;
f(x) =3log2x;
n(t)=t3-3t2-9t+30;
f(x)=-sin(1.5π-x);
y=log0.5(3-4x);
f(x)=x3 0.23x-2 ;
f(x)=ln(0.5x)-x2.

+ 2;
p (x)= 24cos(8x+4);
f (x)= 0.4x-5 ln0.4;
y =3x2e2+3x(x+1);
f

(x)= -2e-4-2x + .

f (x)= 5;
g (x)= -sinx;
f (x)= ;
n (t)= 3t2-6t-9;
f (x)=- sinx;
y = ;
f (x)= 3x2 0.23x-2(1+xln0.2);
f (x)= -2x ;