Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему к уроку в 9 классе на тему Математическое моделирование при решении текстовых задач

Содержание

Тема урокаРешение прикладных задач.Классификация текстовых задачЗадачи на движение.Задачи на смеси и сплавы. Задачи на проценты.Задачи на работу.
Джордж Пойа Тема урокаРешение прикладных задач.Классификация текстовых задачЗадачи на движение.Задачи на смеси и сплавы. Этапы решения прикладных задач:Построение математической модели.Решение математической задачи.Анализ полученного результата, исходя из содержания прикладной задачи. Математическая модельЧисловые и буквенные выражения.Формулы.Уравнения.Неравенства.Функции и графики. Что это? Ещё одна модель с помощью которой можно удобно и наглядно представить информацию данную в условии задачи.Таблицы Цель урока:научиться использовать таблицы для решения задач алгебраическим способом. Основные принципы работы с таблицейТаблица должна быть «живой», действенной моделью, создаваться самим Использование таблиц для решения текстовых задач по математике Задачу прочтиНемного помолчиПро себя повториЕщё раз прочтиНет объёма работы, за 1 Задачи на смеси и сплавыУдобно решать с использованием следующих вспомогательных средств: каждая Задачи для самостоятельной работы (Заполните таблицы и составьте уравнения) Задача 1. Решение задачи 1. Задача на работу. Решение задачи 2. Задача на совместную задачу. Решение задачи 3. Задача на концентрацию Решение задачи 4 . Задача на движение. Задачи «на бассейн»Задача 1.Первая труба пропускает на 4 литра воды в минуту Решение задачи 1 Пусть х литров воды за 1 минуту пропускает Пусть за х часов наполнит весь бассейн, «работая» только первая труба, за Рефлексия 1. Перечислите типы задач, которые мы рассмотрели на уроке.2. Назовите Домашнее заданиеN из учебника 486, 493, 497.Подготовить решения 2 задач из тестов ОГЭ по данной теме. Всем спасибо !
Слайды презентации

Слайд 2 Тема урока

Решение прикладных задач.

Классификация текстовых задач
Задачи на движение.
Задачи

Тема урокаРешение прикладных задач.Классификация текстовых задачЗадачи на движение.Задачи на смеси и

на смеси и сплавы.
Задачи на проценты.
Задачи на работу.

Слайд 3 Этапы решения прикладных задач:
Построение математической модели.

Решение математической задачи.

Анализ

Этапы решения прикладных задач:Построение математической модели.Решение математической задачи.Анализ полученного результата, исходя из содержания прикладной задачи.

полученного результата, исходя из содержания прикладной задачи.

Слайд 4 Математическая модель

Числовые и буквенные выражения.
Формулы.
Уравнения.
Неравенства.
Функции и графики.

Математическая модельЧисловые и буквенные выражения.Формулы.Уравнения.Неравенства.Функции и графики.

Слайд 5 Что это?

Что это? - способ структурирования

- способ

структурирования данных. Представляет собой распределение данных по однотипным строкам и столбцам.

(из лат. tabula — доска)

Таблица

? ? ?

Слайд 6 Ещё одна модель с помощью которой можно удобно

Ещё одна модель с помощью которой можно удобно и наглядно представить информацию данную в условии задачи.Таблицы

и наглядно представить информацию данную в условии задачи.

Таблицы

Слайд 7 Цель урока:

научиться использовать таблицы для решения задач алгебраическим

Цель урока:научиться использовать таблицы для решения задач алгебраическим способом.

способом.

Слайд 8 Основные принципы работы с таблицей
Таблица должна быть «живой»,

Основные принципы работы с таблицейТаблица должна быть «живой», действенной моделью, создаваться

действенной моделью, создаваться самим человеком.

Принцип единообразия. Величины, занесенные в

первый и третий столбики таблицы, должны находиться в прямопропорциональной зависимости.

Таблица должна помогать анализу данных, не обременять решение.

Слайд 9 Использование таблиц для решения текстовых задач по математике

Использование таблиц для решения текстовых задач по математике

Слайд 10

Слайд 11 Задачу прочти
Немного помолчи
Про себя повтори
Ещё раз прочти
Нет

Задачу прочтиНемного помолчиПро себя повториЕщё раз прочтиНет объёма работы, за

объёма работы, за 1 прими
Объём выполненной работы выражают как

часть этой единицы!
Данные в таблицу занеси
Уравнение запиши
Уравнение реши
При совместной работе производительности складываются и приравниваются к общей!

Что необходимо делать? (при решении задач на работу)

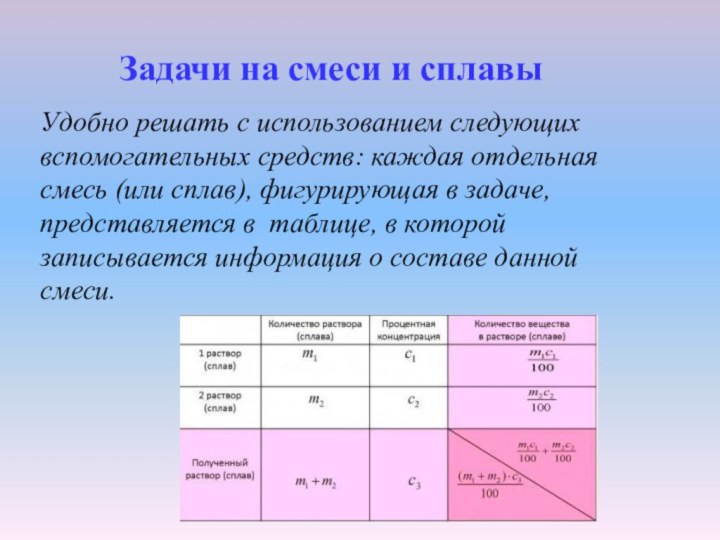
Слайд 12 Задачи на смеси и сплавы
Удобно решать с использованием

Задачи на смеси и сплавыУдобно решать с использованием следующих вспомогательных средств:

следующих вспомогательных средств: каждая отдельная смесь (или сплав), фигурирующая

в задаче, представляется в таблице, в которой записывается информация о составе данной смеси.

Слайд 13 Задачи для самостоятельной работы (Заполните таблицы и составьте уравнения)
Задача

Задачи для самостоятельной работы (Заполните таблицы и составьте уравнения) Задача

1. Задача на работу.
Николай рассчитал, что он сможет

хорошо приготовиться к экзамену, если будет до экзамена решать по 12 задач в день. Однако ежедневно он перевыполнял свою норму на 8 задач и уже за 5 дней  до экзамена решил на 20 задач больше, чем планировал первоначально. Сколько задач решил Николай?
Задача 2. Задача на совместную работу.
На двух копировальных машинах, работающих одновременно, можно сделать копию пакета документов за 10 мин. За какое время можно выполнить эту работу на каждой машине в отдельности, если известно, что на первой машине её можно сделать на 15 мин быстрее, чем на второй?
Задача 2. Задача на концентрацию.
Сколько граммов воды надо добавить к 80 г раствора, содержащего 15% соли, чтобы получить 12%-ный раствор?
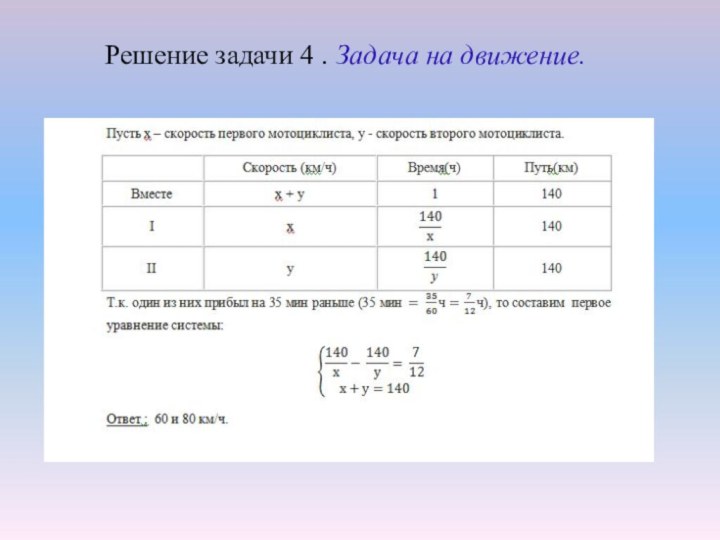
Задача 4. Задача на движение.
Два мотоциклиста выехали одновременно из городов А и В навстречу друг другу. Через час они встретились и, не останавливаясь, продолжили двигаться. Один из них прибыл в город А на 35 мин раньше, чем второй – в город В. Найдите скорость каждого мотоциклиста, если расстояние между городами составляет 140 км.


Слайд 14 Решение задачи 1. Задача на работу.

Решение задачи 1. Задача на работу.

Слайд 15 Решение задачи 2. Задача на совместную задачу.

Решение задачи 2. Задача на совместную задачу.

Слайд 16 Решение задачи 3. Задача на концентрацию

Решение задачи 3. Задача на концентрацию

Слайд 17 Решение задачи 4 . Задача на движение.

Решение задачи 4 . Задача на движение.

Слайд 18 Задачи «на бассейн»
Задача 1.
Первая труба пропускает на 4

Задачи «на бассейн»Задача 1.Первая труба пропускает на 4 литра воды в

литра воды в минуту меньше, чем вторая труба. Сколько

литров в минуту пропускает первая труба, если бассейн объёмом 480 литров она заполняет на 20 минуты дольше, чем вторая труба?


Задача 2
Первая труба и вторая, работая вместе, наполняют бассейн за 36 часов, первая и третья – за 30 часов, вторая и третья – за 20 часов. За сколько часов наполнят бассейн три трубы, работая вместе?


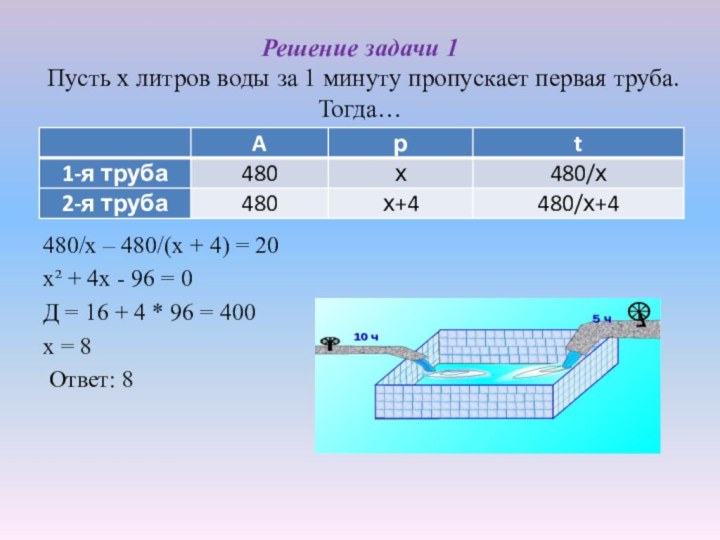
Слайд 19 Решение задачи 1 Пусть х литров воды за 1

Решение задачи 1 Пусть х литров воды за 1 минуту

минуту пропускает первая труба. Тогда…



480/х – 480/(х + 4)

= 20
х² + 4х - 96 = 0
Д = 16 + 4 * 96 = 400
х = 8
Ответ: 8

Слайд 20 Пусть за х часов наполнит весь бассейн, «работая»

Пусть за х часов наполнит весь бассейн, «работая» только первая труба,

только первая труба, за у часов – вторая труба,

за z часов – третья труба. Тогда…

Решение задачи 2 «на бассейн»

1 т

2 т

х

1

1

у

z

Вместе
1 и 2

1

Ответ: 18 часов.

3 т

36

1

Вместе
1 и 3

1

Вместе
2 и 3

1

30

20

=

=

=

А

N

t

Слайд 21 Рефлексия

1. Перечислите типы задач, которые мы рассмотрели на

Рефлексия 1. Перечислите типы задач, которые мы рассмотрели на уроке.2.

уроке.
2. Назовите этапы решения задач.
3. Какие математические модели используют

при решении задач?
4. Какова был цель урока?
5. Сколько задач из 6 предложенных, удалось решить самостоятельно?

Слайд 22 Домашнее задание


N из учебника 486, 493, 497.
Подготовить решения

Домашнее заданиеN из учебника 486, 493, 497.Подготовить решения 2 задач из тестов ОГЭ по данной теме.

2 задач из тестов ОГЭ по данной теме.

Слайд 23

  • Имя файла: prezentatsiya-k-uroku-v-9-klasse-na-temu-matematicheskoe-modelirovanie-pri-reshenii-tekstovyh-zadach.pptx
  • Количество просмотров: 304
  • Количество скачиваний: 25
- Предыдущая Блокада Ленинграда
Следующая - Презентация по физической культуре на тему Упражнения выполняемые со страховкой и без (7 класс)

Похожие презентации

Презентация по алгебре 7 класс Презентация по алгебре 7 класс 179
Интеллектуальная игра Что? Где? Когда? Интеллектуальная игра Что? Где? Когда? 157
Функция у = k / х. Функция у = k / х. 147
Размещение элементов Размещение элементов 194
Презентаөия по алгебре на темуКвадратные уравнения Презентаөия по алгебре на темуКвадратные уравнения 170
Презентация к уроку 9 класс График функции Презентация к уроку 9 класс График функции 147
роковое число 666 роковое число 666 158
Решение алгебраических уравнений Решение алгебраических уравнений 163
Уравнения Уравнения 137
Презентация Занимательные факты из жизни великих математиков Презентация Занимательные факты из жизни великих математиков 203
Подготовка к контрольной работе №1 по геометрии Подготовка к контрольной работе №1 по геометрии 170
Презентация по алгебре и началам анализа на тему Арксинус. Решение уравнения вида sint=a Презентация по алгебре и началам анализа на тему Арксинус. Решение уравнения вида sint=a 62
Презентация к уроку алгебры на тему Первообразная в соответствии с ФГОС Презентация к уроку алгебры на тему Первообразная в соответствии с ФГОС 170
22.02.2010г.Формулы дифференцирования 22.02.2010г.Формулы дифференцирования 147
Производная Производная 176
Решу ВПР: простейшие текстовые задачи. Часть 6 Решу ВПР: простейшие текстовые задачи. Часть 6 58
Презентация по геометрии Пропорциональные отрезки в прямоугольном треугольнике Презентация по геометрии Пропорциональные отрезки в прямоугольном треугольнике 155
Презентация к уроку по теме Геометрический смысл производной Презентация к уроку по теме Геометрический смысл производной 88
Презентация урока математики в 7 классе коррекционной школы Сложение и вычитание обыкновенных дробей с разными знаменателями Презентация урока математики в 7 классе коррекционной школы Сложение и вычитание обыкновенных дробей с разными знаменателями 215
Координаты плоскости Координаты плоскости 166
Презентация по алгебре и начало анализа на тему Арксинус и арккосинус(10 класс) Презентация по алгебре и начало анализа на тему Арксинус и арккосинус(10 класс) 110
Презентация по алгебре на тему Линейная функция (7 класс) Презентация по алгебре на тему Линейная функция (7 класс) 188
РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ на движение. С задачи 2 РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ на движение. С задачи 2 179
Презентация к уроку алгебры Решение неравенств методом интервалов Презентация к уроку алгебры Решение неравенств методом интервалов 171
Презентация по математике Числа Фибоначчи Презентация по математике Числа Фибоначчи 175
Арифметические действия над положительными и отрицательными числами Арифметические действия над положительными и отрицательными числами 145
Числовые неравенства и числовые промежутки Числовые неравенства и числовые промежутки 185
Презентация по математике на тему Умножение и деление комплексных чисел, заданных в алгебраической форме Презентация по математике на тему Умножение и деление комплексных чисел, заданных в алгебраической форме 176
Презентация по математике Теорема Виета Презентация по математике Теорема Виета 211
Презентация к уроку математики по теме Многочлены Презентация к уроку математики по теме Многочлены 172